参考资料:
Variational Discriminator Bottleneck
论文阅读·Variational Discriminator Bottleneck
【信息论】互信息I(X;Y)中H(X)怎么推导出来——p(x)怎么变成p(x,y)
简介
该论文是基于生成对抗网络的一种改进,在生成器生成的数据以及真实数据输入判别器前,通过一个编码器对其信息量进行“限流”,达到使训练更加稳定的目的。
此方法不仅可用于计算机视觉领域的GAN中,还能用在逆强化学习,模仿学习等等相类似的网络中,改善训练效果。
预备知识:互信息
在信息论中,我们用信息熵来衡量一个分布无序的程度,例如存在一个分布X(由一连串概率组成,总和为1),其信息熵的计算方式为:
$$
H(X) = E(-log_2 p(x)) = - \sum_x p(x) log_2 p(x)
$$
可以看出,当概率分布越小,越分散,其无序的程度越高,那么$H(X)$就越大。
而联合熵,相当于是一个二维平面上的信息熵,代表了X,Y的分布的无序程度,计算方式是:
$$
H(X,Y) = E[-log_2 p(x_i,y_j)] = -\sum_{i=1}^n \sum_{j=1}^m p(x_i,y_j) log_2 p(x_i,y_j)
$$
X确定下Y的条件熵,是指在确定了事件X的情况下,事件Y的无序程度,计算方式为:
$$
H(Y|X) = \sum_{i=1}^n p(x_i) H(Y|x_i) = \sum_{i=1}^n p(x_i) \sum_{j=1}^m -p(y_j) log_2 p(y_j |x_i) = -\sum_x \sum_y p(x,y) log_2(y|x)
$$
互信息指的是,知道事件X的情况下,对事件Y无序程度减少的量,记为$I(X;Y)$,计算方式为:
$$
I(X;Y) = H(X) - H(X|Y) \
= -\sum_x p(x) \log_2 p(x) + \sum_x \sum_y p(x,y) \log_2 p(x|y) \
= - \sum_x \sum_y p(x,y)(log_2 p(x) - log_2p(x|y)) \
= \sum_x \sum_y p(x,y)( log_2p(x|y) - log_2 p(x)) \
= \sum_x \sum_y p(x,y) log_2 \frac{p(x|y)}{p(x)} \
= \sum_x \sum_y p(x,y) log_2 \frac{p(x,y)}{p(x)p(y)} = I(Y;X)
$$
这个公式又能化为KL散度的形式:
$$
I(X;Y) = \sum_y p(y) \sum_x p(x|y) log_2 \frac{p(x|y)}{p(x)} \
= \sum_y p(y) D_{KL}(p(x|y) \ || \ p(x)) \
= E_Y [ D_{KL}(p(x|y) \ || \ p(x)]
$$
按照我们之前的定义,无序程度减少的量就是不知道Y之前X的无序程度减去知道Y之后X的无序程度,互信息通常也分布改变之后信息传输量的多少。在本论文中,就是通过控制这个信息量的传输对训练过程进行改善的。
Variational Discriminator Bottleneck

现在我们回顾生成对抗网络的内容(GAN),如上图所示,生成器生成的数据和真实数据一起,经过一个编码器,一起送进判别其中,让其判别真假,训练他们相互对抗,减低对应的Loss函数,就能达到对应的效果:
$$
E_{x ~ P^*(x)}[-log(D(x))] + E_{x~G(x)}[-log(1-D(x))]
$$
判别器的目标是让这个Loss函数越小越好,而生成器的目标是让它越大越好,从而形成对抗的关系。
然而,判别器只需要判别真假,但生成器却要生成相对复杂得多的数据来欺骗判别器,因此判别器的训练要比生成器简单很多,这种训练步调上的不一致会导致训练不稳定,使生成器的效果难以提升,因此我们需要给判别器“增加难度”,方法就是限制给它的信息量。也就是通过限制互信息的大小达到给判别器“增加难度”的目的。
我们把输入Encoder之前的分布称为X,输出的分布称为Z,因此我们需要限制$I(X;Z)$:
因此我们需要加入一个限制项,判别器的优化目标变为:
$$
J(D,E) = \min_{D,E} E_{x ~ P^*(x)}[E_{z~E(z|x)}[-log(D(x))]] + E_{x~G(x)}[E_{z~E(z|x)}[-log(1-D(x))]] \
s.t. E_{x ~ \tilde P(x)}[KL[p(z|x) || r(z)]] \leq I_c
$$
然而这样的表示方法在编程上不好实现,因此我们可以写成:
$$
J(D,E) = \min_{D,E} \max_{\beta \geq0} E_{x ~ P^*(x)}[E_{z~E(z|x)}[-log(D(x))]] + E_{x~G(x)}[E_{z~E(z|x)}[-log(1-D(x))]] + \
\beta E_{x ~ \tilde P(x)}[KL[p(z|x) || r(z)] - I_c]
$$
更新方式为:
$$
D,E \leftarrow \arg \min_{D,E} L(D,E,\beta) \
\beta \leftarrow \max(0,\beta + \alpha_{\beta} (E_{x ~ \tilde P(x)}[KL[p(z|x) || r(z)] - I_c]))
$$
当$E_{x ~ \tilde P(x)}[KL[p(z|x) || r(z)]] < I_c$ 时,$\beta$慢慢变成0,式子后面一项不起作用,网络正常更新;当$E_{x ~ \tilde P(x)}[KL[p(z|x) || r(z)]] > I_c$时,$\beta$会慢慢增大,$\beta$越大会使得更新的梯度越大,使得梯度下降时的互信息下降越快,回到小于$I_c$的水平,如此循环反复。
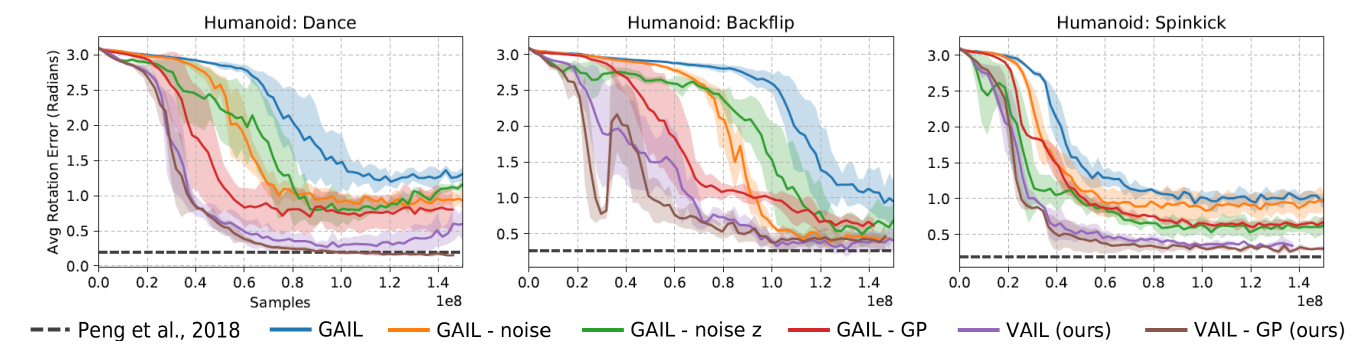
可以看到,改善的效果是十分显著的。