论文:QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning
参考博客:多智能体强化学习入门(五)——QMIX算法分析、多智能体强化学习入门QMIX
参考书籍:《深度强化学习学术前沿与实战应用》
MARL中如何表示和使用动作价值函数使得系统达到一个均衡稳态是多智能体系统的目标。
IQL让每个智能体单独定义一个函数$Q_a$。这种方法不能明确表示智能体之间的相互作用,并且可能不会收敛,因为每个智能体的学习都被其他智能体的探索和学习混淆。
另一种是学习一个完全集中式的动作价值函数,即反事实多智能体(counterfactual Multi-Agent COMA),用它来指导actor-critic框架中的分布策略的优化,但需要on-policy学习,导致样本效率低下,并且存在多个智能体是,训练完全集中的critic是不切实际的。
因此这里采用了QMIX,和VDN一样采用集中式分解Q的方法,处于IQL和COMA之间,但可以表示更丰富的动作价值函数。由于VDN的完全因子分解对于获得分散策略并不是必须的。相反,QMIX只需要确保在Q上执行的全局argmax与在每个Q上执行的一组单独的argmax参数产生相同的结果。因此,只需要求对$Q^{\pi}$于每个$Q_a$之间存在单调约束,即:
$$
\frac{\delta Q^{\pi}}{\delta Q_a} \geq 0, \ \forall a
$$
不同于VDN中简单的总和,QMIX由代表每个$Q_a$的智能体网络和将它们组合到$Q^{\pi}$中的混合网络组成,以复杂的非线性方式确保集中式和分散式策略之间的一致性。同时,它通过限制混合网络具有正权重来强制执行上式的约束。因此,QMIX可以表示复杂的集中式动作价值函数,其中包含一个因式表示,可以很好扩展智能体的数量,并允许通过线性时间的argmax操作轻松得到分散策略。
QMIX提出为了确保一致性,只需要确保在$Q^{\pi}$上执行的全局argmax产生与在每个$Q_a$上执行的一组单独argmax操作有相同的结果:
$$
argmax_u Q^{\pi} (\tau,u) = (argmax_{u_1}Q_1(\tau_1,u_1) … argmax_{u_n}Q_n(\tau_n,u_n))
$$
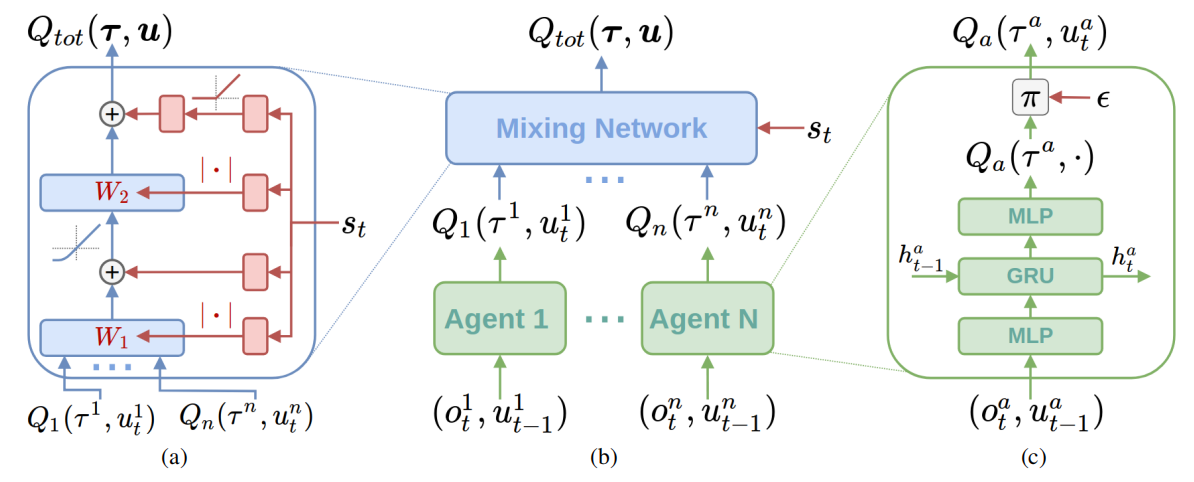
QMIX使用由智能体网络、混合网络和一组超网络组成的体系结构来代表$Q^{\pi}$。它采用一个混合网络对单智能体局部值函数进行合并,并在训练学习过程中加入全局状态信息辅助,来提高算法性能。
图(c)表示每个智能体采用一个DRQN来拟合自身的Q值函数的到 $Q_i(\tau_i,a_i,\theta_i)$ ,DRQN循环输入当前的观测 $o_{i,t}$ 以及上一时刻的动作 $a_{i,t-1}$来得到Q值。
图(b)表示混合网络的结构。其输入为每个DRQN网络的输出。为了满足上述的单调性约束,混合网络的所有权值都是非负数,对偏移量不做限制,这样就可以确保满足单调性约束。
为了能够更多的利用到系统的状态信息 $s_t$ ,采用一种超网络(hypernetwork),混合网络的权重由单独的超网络产生。将状态 $s_t$ 作为输入,输出为混合网络的权值及偏移量。为了保证权值的非负性,采用一个线性网络以及绝对值激活函数保证输出不为负数。
对偏移量采用同样方式但没有非负性的约束,混合网络最后一层的偏移量通过两层网络以及ReLU激活函数得到非线性映射网络。由于状态信息 $s_t$ 是通过超网络混合到 $Q_{tot}$ 中的,而不是仅仅作为混合网络的输入项,这样带来的一个好处是,如果作为输入项则 $s_t$ 的系数均为正,这样则无法充分利用状态信息来提高系统性能,相当于舍弃了一半的信息量。
于DQN类似,最终的Loss函数计算为:
$$
L(\theta) = \sum_{i=1}^b [(y_i^{\pi} - Q^{\pi}(\tau,a,s;\theta))^2]
$$
$$
y_i^{\pi} = r + \gamma \max_{a’}Q^{\pi} (\tau’,a’,s’;\theta^-)
$$
代码分析
QMIX主要是在模型上的改进,因此这里只列出模型的代码:
写法1:
# 这里把两个网络模型合起来计算了
class QMIXNet(nn.Module):
def __init__(self,num_agents,action_space,state_shape,
agent_shape,agent_hidden_size,mixing_hidden_size):
super(QMIX,self).__init__()
self.num_agents = num_agents
self.action_space = action_space
self.state_shape = state_shape
self.agent_shape = agent_shape
self.agent_hidden_size = agent_hidden_size
self.mixing_hidden_size = mixing_hidden_size
self.agent_ff_in = nn.Linear(self.agent_shape,self.agent_shape)
self.agent_net = nn.GRU(self.agent_shape,self.agent_hidden_size)
self.agent_ff_out = nn.Linear(self.agent_hidden_shape,self.aciton_space)
self.hyper_net1 = nn.Linear(self.state_shape,self.num_agents * self.mixing_hidden_size)
self.hyper_net2 = nn.Linear(self.state_shape, self.mixing_hidden_size)
def forward(self,global_state,agent_obs):
# 计算单智能体的Q值
q_n = self.agent_ff_in(agent_obs)
q_n = self.agent_net(q_n)
q_n = self.agent_ff_out(q_n).max(dim = 1)[0]
# 输入状态s到网络中,输出计算单智能体Q值在总Q值的权重参数,这里没计算偏置b
w1 = self.hyper_net1(global_state).abs()
w2 = self.hyper_net2(global_state).abs()
w1 = w1.view(self.num_agents,self.mixing_hidden_size)
w2 = w2.view(self.mixing_hidden_size,1)
# ELU激活函数:ELU(x) = max(0,x) + min(0,α*(exp(x) - 1))
# torch.mm为两个矩阵相乘
q_tot = F.elu(torch.mm(q_n,w1))
q_tot = F.elu(torch.mm(q_tot,w2))
return q_tot写法2:
# 这里分开成两个网络模型,一个分给各个智能体用,一个组成总Q值
# RNN类对应DRQN,可以计算各个智能体的Q值,forward的输出第一个是Q值,第二个是传给下一个RNN的隐藏值。
class RNN(nn.Module):
# Because all the agents share the same network, input_shape=obs_shape+n_actions+n_agents
def __init__(self, input_shape, args):
super(RNN, self).__init__()
self.args = args
self.fc1 = nn.Linear(input_shape, args.rnn_hidden_dim)
self.rnn = nn.GRUCell(args.rnn_hidden_dim, args.rnn_hidden_dim)
self.fc2 = nn.Linear(args.rnn_hidden_dim, args.n_actions)
def forward(self, obs, hidden_state):
x = f.relu(self.fc1(obs))
# print(hidden_state.shape,"xxxxx")
h_in = hidden_state.reshape(-1, self.args.rnn_hidden_dim)
# print(h_in.shape,"uuu")
h = self.rnn(x, h_in)
q = self.fc2(h)
print(q)
print(h)
return q, h
class QMixNet(nn.Module):
def __init__(self, args):
super(QMixNet, self).__init__()
self.args = args
# 因为生成的hyper_w1需要是一个矩阵,而pytorch神经网络只能输出一个向量,
# 所以就先输出长度为需要的 矩阵行*矩阵列 的向量,然后再转化成矩阵
# args.n_agents是使用hyper_w1作为参数的网络的输入维度,args.qmix_hidden_dim是网络隐藏层参数个数
# 从而经过hyper_w1得到(经验条数,args.n_agents * args.qmix_hidden_dim)的矩阵
if args.two_hyper_layers:
self.hyper_w1 = nn.Sequential(nn.Linear(args.state_shape, args.hyper_hidden_dim),
nn.ReLU(),
nn.Linear(args.hyper_hidden_dim, args.n_agents * args.qmix_hidden_dim))
# 经过hyper_w2得到(经验条数, 1)的矩阵
self.hyper_w2 = nn.Sequential(nn.Linear(args.state_shape, args.hyper_hidden_dim),
nn.ReLU(),
nn.Linear(args.hyper_hidden_dim, args.qmix_hidden_dim))
else:
self.hyper_w1 = nn.Linear(args.state_shape, args.n_agents * args.qmix_hidden_dim)
# 经过hyper_w2得到(经验条数, 1)的矩阵
self.hyper_w2 = nn.Linear(args.state_shape, args.qmix_hidden_dim * 1)
# hyper_w1得到的(经验条数,args.qmix_hidden_dim)矩阵需要同样维度的hyper_b1
self.hyper_b1 = nn.Linear(args.state_shape, args.qmix_hidden_dim)
# hyper_w2得到的(经验条数,1)的矩阵需要同样维度的hyper_b1
self.hyper_b2 =nn.Sequential(nn.Linear(args.state_shape, args.qmix_hidden_dim),
nn.ReLU(),
nn.Linear(args.qmix_hidden_dim, 1)
)
def forward(self, q_values, states): # states的shape为(episode_num, max_episode_len, state_shape)
# 传入的q_values是三维的,shape为(episode_num, max_episode_len, n_agents)
episode_num = q_values.size(0)
q_values = q_values.view(-1, 1, self.args.n_agents) # (episode_num * max_episode_len, 1, n_agents) = (1920,1,5)
states = states.reshape(-1, self.args.state_shape) # (episode_num * max_episode_len, state_shape)
w1 = torch.abs(self.hyper_w1(states)) # (1920, 160)
b1 = self.hyper_b1(states) # (1920, 32)
w1 = w1.view(-1, self.args.n_agents, self.args.qmix_hidden_dim) # (1920, 5, 32)
b1 = b1.view(-1, 1, self.args.qmix_hidden_dim) # (1920, 1, 32)
hidden = F.elu(torch.bmm(q_values, w1) + b1) # (1920, 1, 32)
w2 = torch.abs(self.hyper_w2(states)) # (1920, 32)
b2 = self.hyper_b2(states) # (1920, 1)
w2 = w2.view(-1, self.args.qmix_hidden_dim, 1) # (1920, 32, 1)
b2 = b2.view(-1, 1, 1) # (1920, 1, 1)
q_total = torch.bmm(hidden, w2) + b2 # (1920, 1, 1)
q_total = q_total.view(episode_num, -1, 1) # (32, 60, 1)
return q_total


