阅读本文需要有深度强化学习基础,可以翻看我以前的文章:强化学习纲要(周博磊课程)、强化学习实践教学
参考原文:分层强化学习survey ,这篇文章讲的十分全面,重复内容不再赘述。
分层主要解决的是稀疏reward的问题,实际的强化问题往往reward很稀疏,再加上庞大的状态空间和动作空间组合,导致直接硬训往往训不出来,遇到头铁的agent更是如此。我们人类在解决一个复杂问题时,往往会将其分解为若干个容易解决的子问题,分而治之,分层的思想正是来源于此。个人理解目前分层的解决手段大体分两种,一种是基于目标的(goal-reach),主要做法是选取一定的goal,使agent向着这些goal训练,可以预见这种方法的难点就是如何选取合适的goal;另一种方式是多级控制(multi-level control),做法是抽象出不同级别的控制层,上层控制下层,这些抽象层在不同的文章中可能叫法不同,如常见的option、skill、macro action等,这种方式换一种说法也可以叫做时序抽象(temporal abstraction)。
SMDP
SMDP指的是半马尔科夫决策过程。和马尔科夫决策过程中一个状态经过一个action就能到达下一个状态不同,它需要一段时间过后或是多个action才能到达下个状态。它可以分为两种:一种是时间连续的,每经过连续的时间状态发生改变。一种是时间离散的,经过几个时间步之后状态发生改变。分层强化学习研究第二种,并按照离散时间进行建模。
h-DQN
h-DQN也叫hierarchy DQN。是一个整合分层actor-critic函数的架构,可以在不同的时间尺度上进行运作,具有以目标驱动为内在动机的DRL。该模型在两个结构层次上进行决策:顶级模块(元控制器)接受状态并选择目标,低级模块(控制器)使用状态和选择的目标来进行决策。我们可以使用不同时间尺度的随机梯度下降来训练模型,以优化预期的未来内在动机(对应控制器)和外部奖励(对应元控制)。这种处理延迟问题的优势是:在获得最佳外在奖励之前具有长状态链的离散随机决策过程。
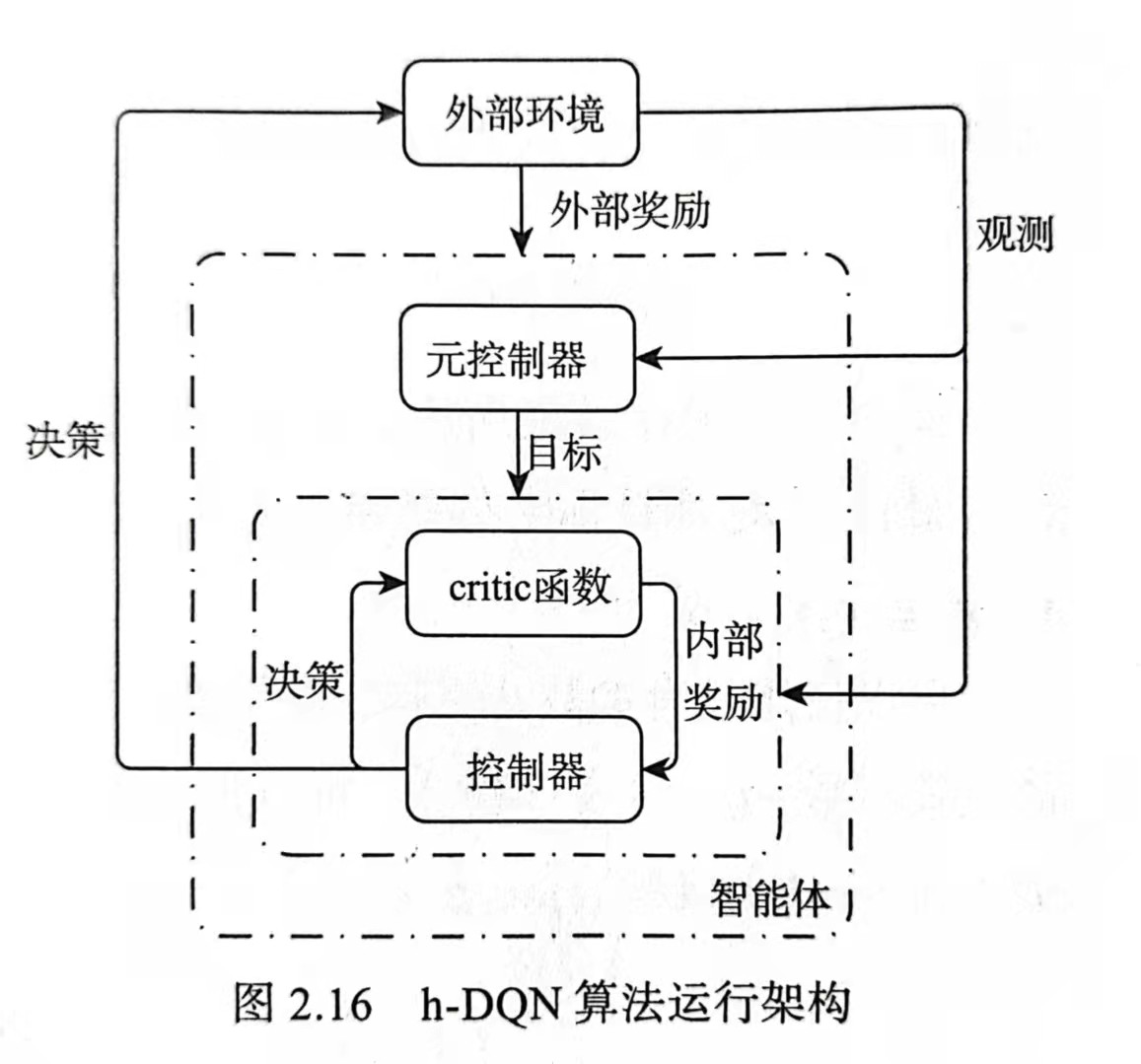
元控制器接收状态并选择目标g,然后控制器使用状态和目标选择动作,目标在接下来的几个时间步中保持不变,直到达到目标或终止状态。内部的critic负责评估是否达到目标,并向控制器提供适当的奖励$r_t(g)$。在这项工作中,进行二元内部奖励的最小化,达到目标为1,否则为0。控制器的目标最大化累计内在奖励,元控制器的目的是优化累计的外在奖励。
控制器Q值函数:
$$
Q_1(s,a;g) = \max_{\pi_{a,g}} E[r_t + \gamma \max_{a_{t+1}}Q_1^*(s_{t+1},a_{t+1};g) | s_t = s,a_t=a,g_t=g,\pi_{a,g}]
$$
元控制器Q值函数:
$$
Q_2(s,g) = \max_{\pi_{a,g}} E[\sum_{t’=t}^{t+N}f_{t’}+ \gamma \max_{g’}Q_2^*(s_{t+N},g’) | s_t = s,g_t=g,\pi_{a,g}]
$$
N表示当前目标下,控制器停止之前的时间步数。
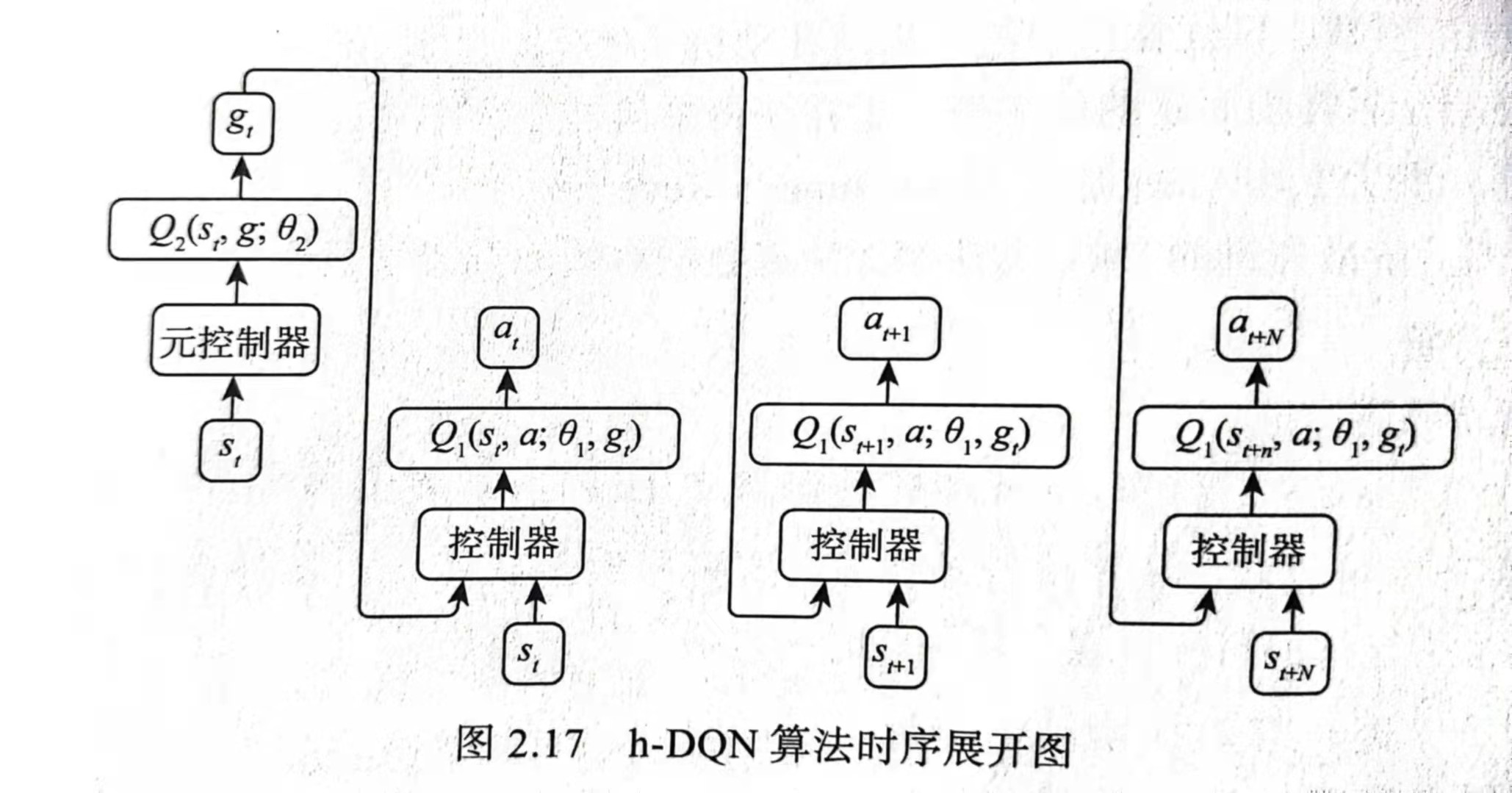
因此需要拟合两个Q函数,而每一Q函数配有一个储存空间,分别是$D_1$储存$(s_t,a_t,g_t,r_t,s_{t+1})$,$D_2$储存$(s_t,g_t,f_t,s_{t+N})$。
对目标的选择上本文的做法是选取游戏画面中某些重要物体的图像作为目标,随state一起传入神经网络,这些目标图像都是人工选择好的。这也是本文的局限。
FuN
https://zhuanlan.zhihu.com/p/46928498
HIRO
https://zhuanlan.zhihu.com/p/46946800



