阅读本文前先了解TRPO算法有助于理解,我对此也写过博客:https://blog.csdn.net/tianjuewudi/article/details/120191097
公式加载不出请查看CSDN:https://blog.csdn.net/tianjuewudi/article/details/120212234
PPO,全名Proximal Policy Optimization,近端策略优化算法。
PPO算法是一种新型的Policy Gradient算法,Policy Gradient算法对步长十分敏感,但是又难以选择合适的步长,在训练过程中新旧策略的的变化差异如果过大则不利于学习。PPO提出了新的目标函数可以再多个训练步骤实现小批量的更新,解决了Policy Gradient算法中步长难以确定的问题。其实TRPO也是为了解决这个思想但是直接求解TRPO这种带约束的问题是十分复杂的,他与PPO算法的效果差不多,但是PPO将KL散度作为惩罚项,更加容易求解。
理论基础:KL散度
KL散度,也称为相对熵,是衡量两个分布差距的计算公式。公式如下:
$$
D_{KL} (p||q) = \sum_{i=1}^N p(x_i) * (\log p(x_i) - \log q(x_i)) = \sum_{i=1}^N p(x_i) * \log \frac{p(x_i)}{q(x_i)}
$$
可以证明这个值大于等于0。当两者分布接近时,这个值会趋近于0,这个值越大,分布差距越大。
从式子中可以看出,KL散度计算的是数据的原分布与近似分布的概率的对数差的期望值。但要注意,散度不具有交换性,不能单纯理解为距离,更准确的说是一个分布相比另一个分布的信息损失。
PPO
PPO也分为Actor的部分和Critic的部分。
首先定义优势函数:
$$
\hat{A_t} = \sum_{t’>t} \gamma^{t’-t}r_{t’} - V_{\phi}(s_t)
$$
更新Actor的部分我们把奖励函数设置成:
$$
J_{PPO}(\theta) = \sum_{t=1}^T \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat{A}t - \lambda KL[\pi{\theta_{old}}|\pi_{\theta}]
$$
- 这里的A其实应该用新策略采样出来计算的Advantage函数,但由于参数改变的不多,我们可以用旧策略的A来近似新策略的A。
- 前面一项的设置是因为我们只能充旧策略中采样而不能从新策略中采样所以做了important Sampling。同时这样做可以把我们的策略从on-policy转变为off-policy,旧策略可以收集很多数据之后,就能用这些数据训练很多次的网络,然后再重新采样。
- 这样当我们新策略的值远大于旧概率时,更新会快一些,但由于后面一项KL散度的存在,不会让概率分布差距过大的新旧策略更新太快,限制了新策略的更新幅度。
而对于Critic部分,我们构建一个输出状态价值的网络,训练网络接近预定值:
$$
L_{BL}(\phi) = -\sum_{t=1}^{T}(\sum_{t’>t} \gamma^{t’-t}r_{t’}-V_{\phi}(s_t))^2
$$
通过梯度递减来训练这个Loss为0.

PPO with Adaptive KL Penalty
我们还发现KL散度还要乘以一个变量,该版本PPO的核心想法就是利用自适应的beta值(adaptive beta):
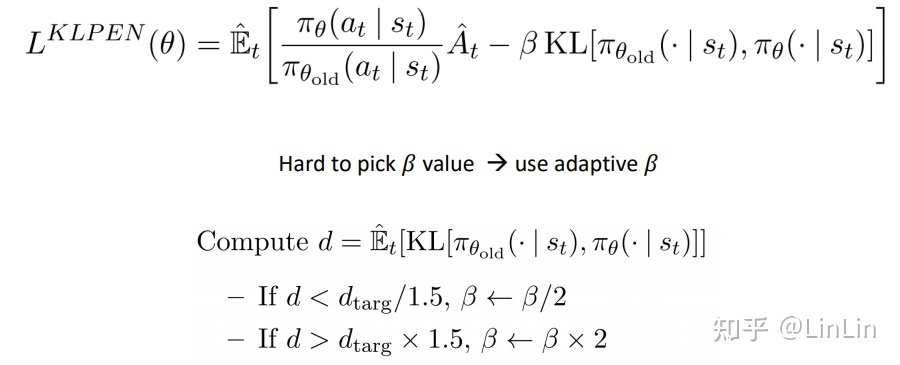
当KL散度大于我们的设定值时,我们需要加大处罚力度,而小于一个设定值时,减小处罚力度,这样使得新旧策略的差距既不会偏大,也不会过小。
PPO with Clipped Objective
这是基于上面PPO的改进,相比于用KL散度来限制策略的更新幅度,我们不如直接限制新旧策略的比例来实现防止其差距过大。这样还减少了KL散度的运算,提升了算法性能。
$$
L^{CLIP}(\theta) = \hat{E_t}[min(r_t(\theta)\hat{A_t},clip(r_t(\theta),1-\epsilon,1+\epsilon)\hat{A_t})]
$$
$$
r_t(\theta) = \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}
$$
这里我们把新旧策略的比例限制在1-ε和1+ε直接,说白了就是在超过这个范围时把新策略直接设定为边界值。
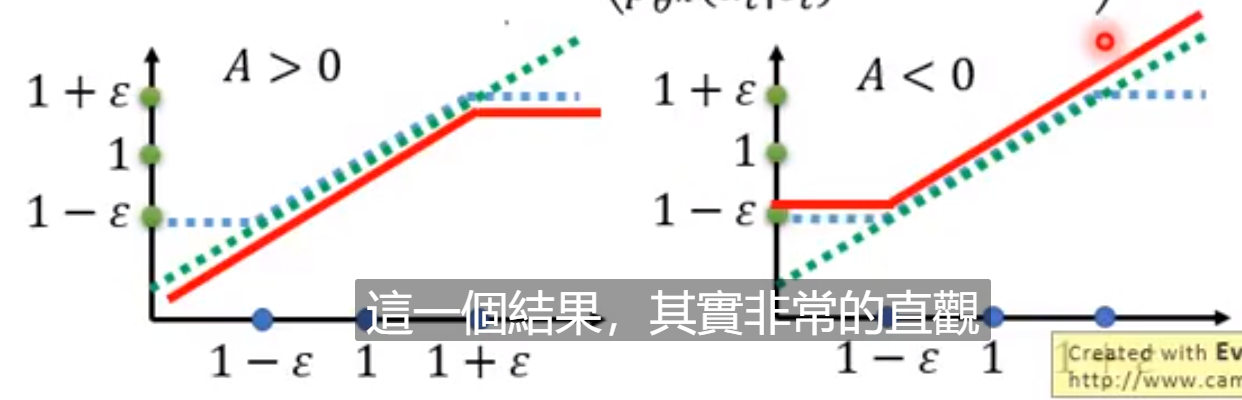
在A为正数的情况下,我们倾向于采取这种行为,因此新策略该行为的概率会慢慢增大,但是又不能大于我们的界限。在A为负数的情况下,我们倾向于摒弃这种行为,但是我们也不能让策略变化范围过大,因此就有了一个下限。



