强化学习之TRPO

​ 注：TRPO算是我至今遇到过的最难理解的算法了，我查了很多资料，花费好几天时间，也未曾理解，向TRPO的一作致敬。。。本文是我的查资料笔记，由于公式过多，可以先学比较重要的PPO。

​ TRPO全称为Trust region policy optimization，意思是信赖域策略优化。

​ TRPO是Policy Gradient的改进算法。Policy Gradient有几个缺陷：当更新步长不合适时，更新的参数所对应的策略是一个更不好的策略，当利用这个更不好的策略进行采样学习时，再次更新的参数会更差，因此很容易导致越学越差，最后崩溃，这是DDPG，A3C等算法都有的问题。所以，合适的步长对于强化学习非常关键。如何找到新的策略使得新的回报函数的值单调增，或单调不减。这是TRPO解决方式就是Trust region，让其在一个安全范围内更新参数。Policy Gradient是一种on-policy的方法，而用off-policy效率会更高，因此TRPO采用了Important Sampling的方法。

---

前期学习流程

​ 为了确保我们每次更新都能得到一个更好的策略，一个方法是把策略$\pi_{i+1}$对应的期望回报函数$\eta(\pi_{i+1})$分解成$\eta(\pi_{i})$加上一个不小于0的项，这样就能保证策略朝着更优的方向前进。

​ 在A2C中，核心思想是加入了一个advantage函数，可以用这个函数来判断新的策略是否优于预期：
$$
A_{\pi}(s_t,a) = E[r(s_t) + \gamma V_{\pi}(s_{t+1}) - V(s_t)]
$$
下面推导一个旧策略回报$\eta(\pi)$和新策略回报$\eta(\tilde{\pi})$关系重要公式：
$$
E[\sum_{t=0}^{\infty} \gamma^t A_{\pi}(s_t,a_t)] \
= E[\sum_{t=0}^{\infty} \gamma^t(r(s_t) + \gamma V_{\pi}(s_{t+1}) - V(s_t))] \
=E[-V_{\pi}(s_0) + \sum_{t=0}^{\infty} \gamma^t r(s_t)] \
= - \eta(\pi) + \eta(\tilde{\pi})
$$
因此：
$$
\eta(\tilde{\pi}) = \eta(\pi) + E[\sum_{t=0}^{\infty} \gamma^t A_{\pi}(s_t,a_t)]
$$

根据Advantage函数的相关知识，判断新策略是否优于旧策略的标准是：

$$
\bar{A}(s) = \sum_a \tilde{\pi}(a|s)A_{\pi}(s,\tilde a) \geq 0
$$
继续推导：

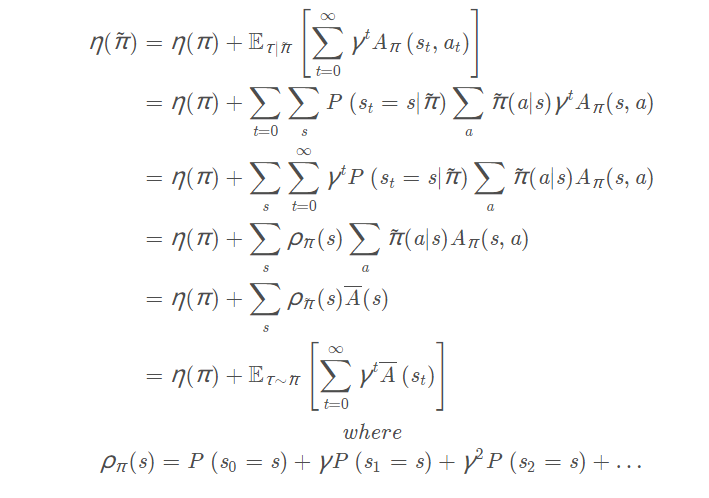
这个公式没法应用，这里s是由新分布产生的，对新分布有很强的依赖性。这个公式其实在应用中完全无法达到，因为我们是为了得到新的策略，所以这里的其他项完全无从所知。

这里实际用转态s的动作优势回报A(s,a)期望$\bar{a}(s)$来代替优势回报$A(s,a)$

现在得到：
$$
\eta(\tilde{\pi}) = \eta(\pi) + E_{\tau|\pi}[\sum_{t=0}^{\infty} \gamma^t \bar A_{}(s_t)]
$$
现在研究一下$\bar{A}(s_t)$
$$
\bar A(s) = \sum_{\tilde a} \tilde{\pi}(a|s)A_{\pi}(s,\tilde a)\
= E[A_{\pi}(s,\tilde a)]\
= E[A_{\pi}(s,\tilde a) - A_{\pi}(s,a)]\
= P(a \neq \tilde a |s) E[A_{\pi}(s,\tilde a) - A_{\pi}(s,a)]\ +P(a = \tilde a |s) E[A_{\pi}(s,\tilde a) - A_{\pi}(s,a)]\
=P(a \neq \tilde a |s) E[A_{\pi}(s,\tilde a) - A_{\pi}(s,a)]
$$
结论：

假设 当智能体所处状态为s的时候新的策略$ \tilde{\pi} $和旧的策略π以α的概率(P ( a ≠ a ~ ∣ s )选择不同的动作，以1-α的概率(P ( a = a ~ ∣ s ) ) 是选择相同的策略
$$
π_ {n e w} ( a ∣ s ) = ( 1 − α ) π_{ o l d }( a ∣ s ) + α π ′ ( a ∣ s )
$$
并且：
$$
|A_{\pi}(s,\tilde a) - A_{\pi}(s,a)| \leq 2\max_{a,s} |A_{\pi}(s,a)|
$$
因此：
$$
|\bar A (s)| = P(a \neq \tilde a |s) E[A_{\pi}(s,\tilde a) - A_{\pi}(s,a)] \leq 2 \alpha max_a |A_{\pi}(s,a)|
$$

定义：对于$n_{t}= 0$表示在在智能体在t时刻之前(t=0,1,2,3,4…t-1)，策略 π ,和策略$\tilde{\pi} $产生的相同状态s，并且采取的每个状态s采取的动作a都相同，此时$P ( n _ { t } = 0 ) = (1-\alpha)^{t}$

对于$n_{t}>0$表示在在智能体在t时刻之前(t=0,1,2,3,4…t-1)，策略 π ,和策略$\tilde{\pi} $产生的相同状态s，但是不同动作a的次数，此时$P ( n _ { t } > 0 ) = 1- (1-\alpha)^{t}$

有：
$$
E_{s_t∼\tilde\pi}[\bar A(s_t)] = P(n_t = 0)E_{s_t ∼ \pi | n_t = 0}[\bar A(s_t)] + P(n_t > 0)E_{s_t ∼ \tilde\pi | n_t > 0}[\bar A(s_t)]
$$

$$
E_{s_t∼\pi}[\bar A(s_t)] = P(n_t = 0)E_{s_t ∼ \pi | n_t = 0}[\bar A(s_t)] + P(n_t > 0)E_{s_t ∼ \pi | n_t > 0}[\bar A(s_t)]
$$

相减得：
$$
E_{s_t∼\tilde\pi}[\bar A(s_t)] -E_{s_t∼\pi}[\bar A(s_t)]\
= P(n_t > 0)(E_{s_t ∼ \tilde\pi | n_t > 0}[\bar A(s_t)] - E_{s_t ∼ \pi | n_t > 0}[\bar A(s_t)])
$$

$$
|E_{s_t∼\tilde\pi}[\bar A(s_t)] -E_{s_t∼\pi}[\bar A(s_t)]|\
= P(n_t > 0)(|E_{s_t ∼ \tilde\pi | n_t > 0}[\bar A(s_t)] - E_{s_t ∼ \pi | n_t > 0}[\bar A(s_t)]|) \
\leq P(n_t > 0)(|E_{s_t ∼ \tilde\pi | n_t > 0}[\bar A(s_t)]| + | E_{s_t ∼ \pi | n_t > 0}[\bar A(s_t)]|) \
\leq P(n_t > 0)4\alpha \max_{s,a}|A_{\pi}(s,a)| \
= 4\alpha (1-(1-\alpha)^t)\max_{s,a}|A_{\pi}(s,a)|
$$

又由前面公式可得：
$$
\eta(\tilde{\pi}) = \sum_s \rho_{\tilde\pi}(s)\sum_a \tilde\pi(a|s)A^{\pi}(s,a) = \eta(\pi) + E_{\tau ∼ \tilde\pi}[\sum_{t=0}^{\infty} \gamma^t A_{\pi}(s_t,a_t)]
$$
令：
$$
L(\tilde{\pi}) = \sum_s \rho_{\pi}(s)\sum_a \tilde\pi(a|s)A^{\pi}(s,a) = \eta(\pi) + E_{\tau ∼ \pi}[\sum_{t=0}^{\infty} \gamma^t A_{\pi}(s_t,a_t)]
$$
则：
$$
|\eta(\tilde{\pi}) -L(\tilde{\pi})| \
= \sum_{t=0}^{\infty}|E_{\tau ∼ \tilde\pi}[ \gamma^t A_{\pi}]-E_{\tau ∼ \pi}[ \gamma^t A_{\pi}]| \
\leq \sum_{t=0}^{\infty} \gamma^t * 4\epsilon \alpha (1-(1-\alpha)^t)\
= 4\epsilon \alpha(\frac{1}{1-\gamma} - \frac{1}{1-\gamma(1-\alpha)}) \
= \frac{4\alpha^2 \gamma \epsilon}{(1-\gamma)^2 + \alpha \gamma(1-\gamma)} \
\leq \frac{4\alpha^2 \gamma \epsilon}{(1-\gamma)^2 }
$$
其中：
$$
\epsilon = \max_{a,s}|A_{\pi} (s,a)|
$$
上面两者只有采用的$\rho_{\pi}(s)$不同，一个是新策略的状态分布，一个是旧策略的状态分布。

因此，最后的公式就推导出来了：
$$
\eta(\pi_{new}) \geq L_{\pi_{old}}(\pi_{new}) - \frac{4\alpha^2 \gamma \epsilon}{(1-\gamma)^2 }
$$

---

那么，如何进行求解：

新策略我们并不知道，也无法求解，所以，需要进行进一步的处理，虽然我们不知道新策略怎么求，但是旧的策略我们是知道的可以用重要性采样（weighted sampling)的方法进行采样把新策略采样出来。

关于重要性采用可参考：https://zhuanlan.zhihu.com/p/41217212
$$
L(\tilde{\pi}) = \eta(\pi)+\sum_s \rho_{\pi}(s)\sum_a \tilde\pi(a|s)A^{\pi}(s,a) = \eta(\pi) + E_{\tau ∼ \pi}[\sum_{t=0}^{\infty} \gamma^t A_{\pi}(s_t,a_t)]
$$
通过重要性采样得：
$$
L(\tilde{\pi}) = \eta(\pi)+E_{s～\rho_{\theta},a～\pi_{\theta}} [\frac{\tilde\pi(a|s)}{\pi_{\theta_{}}}A_{\theta}(s,a)]
$$

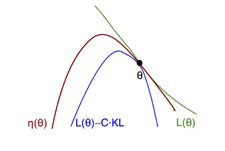
最终的工程实践版本：

---

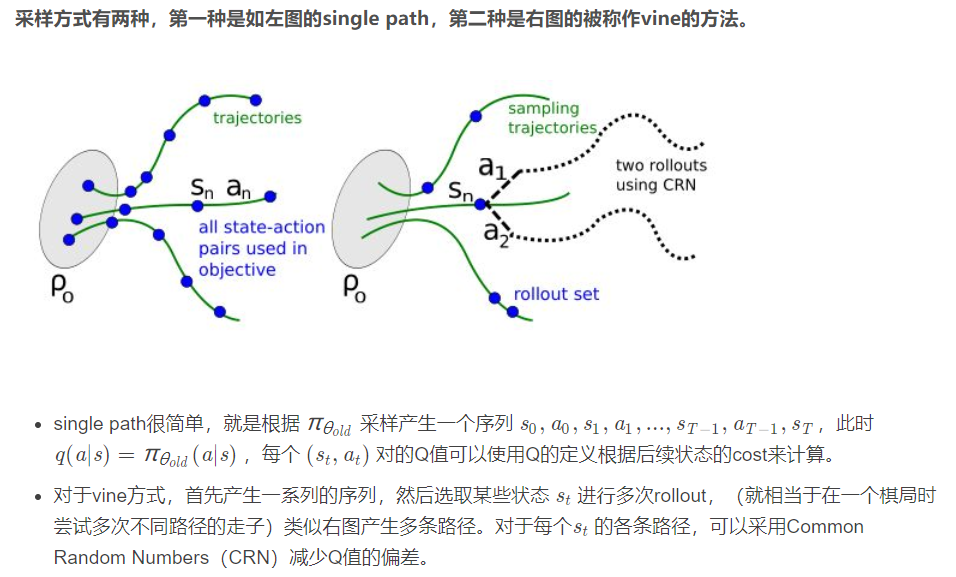
TRPO中存在四个技巧：

1. 在原式中计算$\rho_{\pi}(s)时，我们需要新的策略，而新策略目前还未知，因此，我们可以利用旧策略来代替新策略，因为两者相差并不是很大。
2. 利用重要性采样处理动作分布。

参考论文：

1.人工智能Paper解读之强化学习TRPO算法

2.强化学习–信赖域系方法：TRPO、PPO（附适合初学者阅读的完整PPO代码连接）

补充

TRPO算法重复着两个步骤：

1. 近似：我们构建一个$L(\theta|\theta_{old})$函数，在信赖域内近似于价值函数$J(\theta)$。
2. 最大化：在信赖域内，找到一组新的参数，使得$L(\theta|\theta_{old})$最大化。

近似：

$$
V_{\pi}(s) = \sum_a \pi(a|s;\theta) * Q_{\pi}(s,a) \
= \sum_a \pi(a|s;\theta_{old})\frac{\pi(a|s;\theta)}{\pi(a|s;\theta_{old})} * Q_{\pi}(s,a) \
= E_{A～\pi(a|s;\theta_{old})}[\frac{\pi(a|s;\theta)}{\pi(a|s;\theta_{old})} * Q_{\pi}(s,a)]
$$

$$
J(\theta) = E_S[V_{\pi}(S)] \
= E_{S,A}[\frac{\pi(A|S;\theta)}{\pi(A|S;\theta_{old})} * Q_{\pi}(S,A)]
$$

这是TRPO的最重要的公式。

在实际运用中，我们做蒙特卡洛近似，如果对于旧策略，我们收集到的数据如下：
$$
s_1,a_1,r_1,s_2,a_2,r_2,…,s_n,a_n,r_n
$$
公式改变如下：
$$
L(\theta|\theta_{old})
= \frac{1}{n}\sum_{i=1}^{n}\frac{\pi(a_i|s_i;\theta)}{\pi(a_i|s_i;\theta_{old})} * Q_{\pi}(s_i,a_i)
$$
这里L就是对J的近似，但这里还无法对L做最大化，原因在于动作价值函数Q我们并不知道是什么，所以我们也要对它做近似。

对于Q是动作价值的期望，我们对它做蒙特卡洛近似，根据折扣函数，可得：
$$
u_i = r_i + \gamma r_{i+1} + \gamma^2r_{i+2}… + \gamma^{n-i} r_n
$$
我们可以用这种计算方式来代替Q。这里我们也可以把Q换成A，也就是优势函数：
$$
A = Q- V = \gamma V_{t+1} + R_{t} - V_t
$$

最大化

有了上面的近似以后，我们对其在信赖域内作最大化：通过调整策略网络参数，使得新的策略网络的奖励期望越大越好。数学公式表达为：
$$
\theta_{new} \leftarrow argmax_{\theta}L(\theta|\theta_{old})
\ s.t. \theta \in N{(\theta_{old})}
$$
有很多方式表达两组参数的距离，这里介绍两种：

1. 二范数距离，即两者的欧式距离，平方和后开方：
   $$
   ||\theta - \theta_{old}|| < \Delta
   $$

2. KL散度：这不是用来衡量两组参数的，而是用来衡量网络输出的概率分布的，概率分布的区别越大，KL散度越大，区别越小越趋近于0，也叫相对熵。

   离散形式
   $$
   KL(P||Q) = \sum P(x)log \frac{P(x)}{Q(x)}
   $$
   连续形式：
   $$
   KL(P||Q) = \int P(x)log \frac{P(x)}{Q(x)}dx
   $$

那么这里的约束条件就是：
$$
\frac{1}{n} \sum_{i=1}^{n} KL[\pi(.|s_i;\theta_{old})||\pi(.|s_i;\theta)] < \Delta
$$
至此，游戏完成了一轮episode，我们进行了一次参数更新，往往更新进行很多次才能得到一个比较好的策略网络。

TRPO的优点是曲线稳定不会剧烈波动，对学习率设置不会太敏感。而且观察到更少的奖励就能达到跟策略梯度算法相同的表现。