Foundation

Overview

这部分内容可以参考我《强化学习概述》的序章。

强化学习的特征可以概括为以下几点：

需要通过在环境中探索来获取对环境的理解。
Agent在环境中获得的奖励是延迟的，在获取奖励的过程中，由于没有反馈，你不知道自己每一步是对是错，优化这个过程是我们需要做的。
时间关联性，获取的数据都是有时间关联的，会使训练非常不稳定。
Agent的行为会影响随后的到的数据。
Agent的任务是让奖励最大化。

强化学习包含以下几个组成部分：

行为策略：也就是决定自己行为的函数，通常可以由神经网络来担任。
价值函数：对自己现在所处的状态进行价值的评估。可以对后面的收益带来多大的影响。
模型：决定了这个世界的运行方式。通过agent当前的状态的行为决定下一个状态，以及可以得到多大的奖励。

当有了行为策略，价值函数和世界模型之后，这三个成分就形成了一个马尔科夫决策过程（MDPs）。这个过程可视化了状态转移和我们采取的行为。

基于agent学习方式不同，我们可以分成两类：

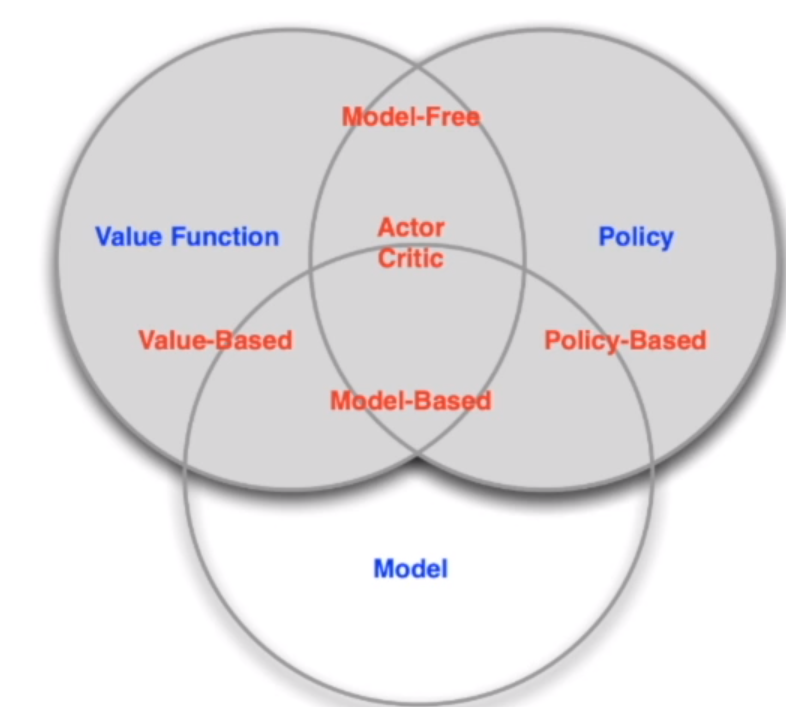
基于价值（Value-based）：依靠价值函数进行学习和决策。
基于策略（Policy-based）：无需构建价值函数，输入状态就可以直接得到下一步动作的概率分布。
Actor-Critic：这是上面两者的结合。既有策略函数（Actor），也有价值函数（Critic）。Actor的任务是对外输出动作并且根据Critic的打分来调整自己的参数来获得更好的输出，使得Critic打分更高。Critic的任务是对Actor的输出做评估（预测），并且通过reward不断调整自己的预测能可能地接近reward。这也就是一个Q网络。

基于agent有没有学习环境的模型进行分类：

基于模型（Model-based）：知道环境的模型，通过学习状态转移采取措施。
无模型（Model-free）：没有环境的模型，通过学习Value Function和Policy Function进行决策。

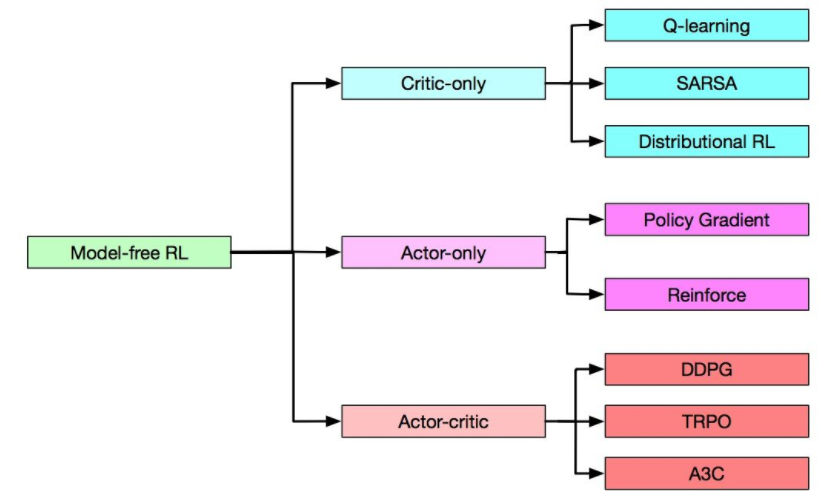
在model-free领域又有三种分类：

强化学习的Exploration和Exploitation：

这是两个很核心的问题，其中Exploration探讨怎么探索环境，尝试不同的行为，期望得到一个最佳的策略。Exploitation探讨不去尝试新的东西，用已知的内容做最好的决策。

Markov Decision Process（MDP）

马尔科夫决策过程是强化学习的基本框架。而Agent和Environment的交互过程，是可以用马尔科夫决策过程表示。其中，环境是全部可以观测的，部分观测问题也可以转换为MDP问题。

一个状态转移符合马尔科夫，意思是下一个状态取决于当前状态，和之前的状态没有关系。

描述状态转移概率，我们可以用状态转移矩阵表示：

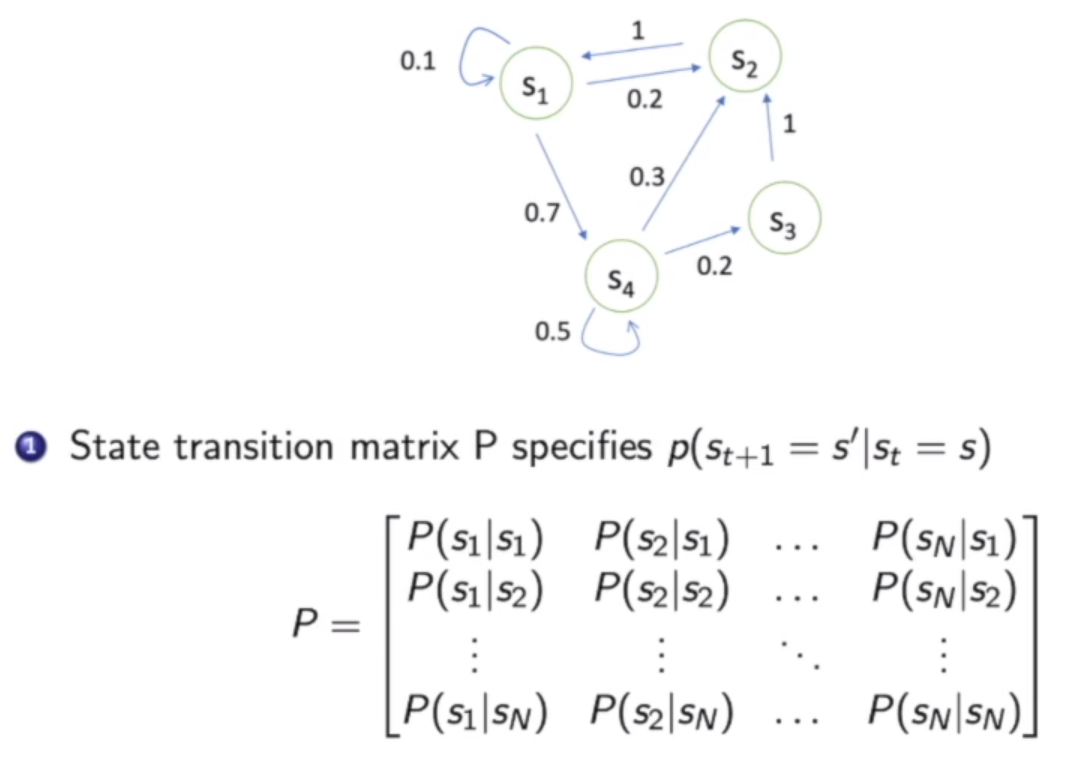
马尔科夫链 Markov Chain / Markov Process（MP）

马尔科夫链可以表示所有的状态转移概率：

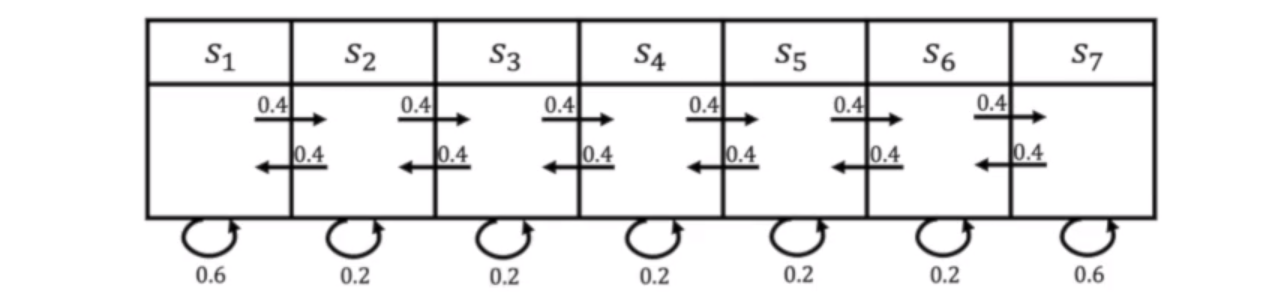
通过对马尔科夫链进行采样，我们可以得到很多从一个起始点开始的一串的轨迹。

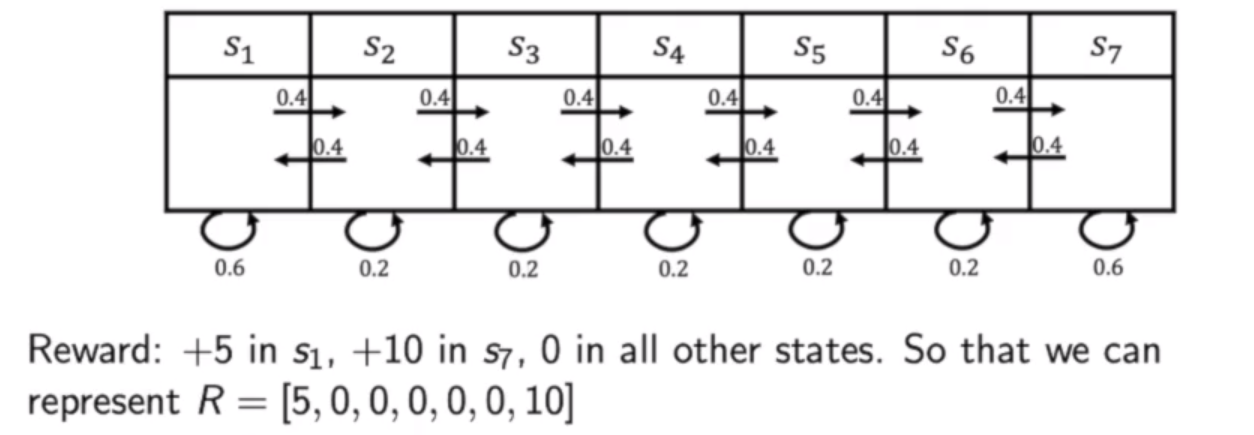
马尔科夫奖励过程 Markov Reward Process（MRP）

马尔科夫奖励过程是一个马尔科夫链加上奖励函数。在马尔科夫链中加入奖励函数，奖励函数是一个期望，表示到达某一个状态时可以获得多大的奖励。

Return and Value Funciton

Horizon

轨迹的长度是由有限个步数决定的。

Return

我们把奖励reward按照一定折扣相加得到。
$$
G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+2} + \gamma^3 R_{t+3} + … + \gamma^{T-t-1} R_{T}
$$

State Value Function for a MRP

$$
V_t(s) = E[G_t|s_t = s] = E[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+2} + \gamma^3 R_{t+3} + \gamma^{T-t-1} R_{T} | s_t = s]
$$

也就是说，一个状态的价值由后面的状态可以得到的reward按一定系数叠加得到，越往后的reward，对当前状态的价值影响越小。

MRP价值函数满足以下贝尔曼等式（Bellman equation）：
$$
V(s) = R(s) + \gamma \sum_{s’ \in S} P(s’|s) V(s’)
$$
也就是说现在状态的价值V（s）和现在的奖励以及下一个所有可能到达的状态的价值V（s’）相关。用矩阵表示：

在状态转移矩阵较小的情况下，我们可以通过直接求逆矩阵就可以得出每一个状态的价值。

MRP价值的解法

第一种解法是动态规划（Dynamic Programming）
第二种解法是蒙泰卡罗评估（Monte-Carlo evaluation）
第三种解法是时序差分（Temporal-Difference Learning）

Monte Carlo Algorithm

蒙泰卡罗算法的做法是直接在某状态开始直接收集多条轨迹的数据，得到多个价值，然后把所有的价值平均起来得到该状态的价值$V_t(s)$，可以说随机的数量足够多，那么$V_t(s)$就会接近真实的价值。

Iterative Algorithm

动态规划的办法是一直迭代Bellman Equation。当迭代到价值稳定时（变化小于某一个值），我们就可以直接输出V（s）。但是我们需要知道状态转移概率。这是一个model-based的方法。

Temporal-Difference Learning

这是前两者的结合。在后面会提到。

马尔科夫决策过程（Markov Decision Process）(MDP)

马尔科夫决策过程比马尔科夫奖励过程多了一个行为（action）。

未来的状态不仅取决于现在的状态，也取决于你所采取的行动。
奖励函数的设置不仅和当前状态有关，和行为也有关。

Policy in MDP

Policy函数决定了在某一个状态中采取的行为，可以输出一个行为的概率（离散控制），也可以是一个连续值（确定动作的连续控制）。而且假设Policy是静态的，也就是说具有时间独立性，不同时间的策略函数不变。

当我们知道MDP和policy π的时候，我们可以把MDP转换为MRP。
$$
P^π(s’|s) = \sum_{a\in A} π(a|s) P(s’|s,a)
$$
也就是说，一个状态转移到另一个状态的概率的计算方式是：Policy可控的决策过程的采取该动作概率 乘上 不可控的该动作下环境选择下一个状态的概率，然后把每个行动的可能性都相加。

奖励函数的计算方式也是分行动的，因为每个行动的reward都不相同：
$$
R^π(s) = \sum_{a \in A} π(a|s) R(s,a)
$$

Value Function for MDP

MDP的价值函数分为状态价值（state-value）和行为价值（action-value）。状态价值由当前的状态决定，而行为价值由当前状态和行动共同决定。有多少行为就有多少行为价值。

状态价值$v^{π}(s)$和行为价值$q^{π}(s)$的关系是：
$$
v^{π}(s) = \sum_{a \in A} π(a|s) q^{π}(s,a)
$$
也就是说状态价值由行为价值按照一定的比例构成。

因此贝尔曼等式有两条，也称Bellman Expection Equation：
$$
v^π (s) = E_{π} [R_{t+1} + \gamma v^{π} (s_{t+1}) | s_t = s]
$$

$$
q^π (s,a) = E_{π} [R_{t+1} + \gamma q^{π} (s_{t+1},A_{t+1}) | s_t = s ,A_t = a]
$$

这两个公式将是写代码更新参数的重点！！！尤其是行为价值公式！

容易得出行为价值公式有：
$$
q^π (s,a) = R_{s}^a + \gamma \sum_{s’ \in S} P(s’|s ,a)v^π(s’)
$$
联立
$$
v^{π}(s) = \sum_{a \in A} π(a|s) q^{π}(s,a)
$$
可以得出：
$$
v^{π}(s) = \sum_{a \in A} π(a|s) ( R_{s}^a + \gamma \sum_{s’ \in S} P(s’|s ,a)v^π(s’))
$$

$$
q^π (s,a) = R_{s}^a + \gamma \sum_{s’ \in S} P(s’|s ,a) \sum_{a \in A} π(a’|s’) q^{π}(s’,a’)
$$

这就是上一个节点与下一个相同属性节点价值之间的关系，使用于知道环境模型的情况下。也就是model-based。

Policy Evaluation

简单的说是计算$v^π(s)$，也叫做价值预测。用这个预测来指导我们的动作选择。

Prediction and Control

预测和控制是MDP的核心问题。

预测：给定MDP<S,A,P,R,γ>和policy π，或者给定MRP$<S,P^π,R^π,γ>$，我们可以对状态价值V进行计算。

控制：给定MDP，寻找最佳的价值函数V和最佳策略π。最佳指的是找π使得V最大。

Dynamic Programming

这两个问题都可以通过动态规划（Dynamic Programming）解决。只要我们可以把问题分解成一个个最优子结构，把子结构解出来，就可以组成一个最优解。我们可以把问题分解成递归的结构，因为状态相连，子状态得到一个值，未来状态也能推算出来，价值函数也就能储存和重用最优解。

或者用MRP公式也能迭代：
$$
v_{t+1} (s) = R^{π}(s) + \gamma P^π (s’|s ,a)v_t(s’)
$$

Find Optimal Policy（重中之重，反复查看）

当我们采取的策略π可以使得行为价值q最大化，那么这个策略就是最佳策略。寻找最佳策略的过程也叫MDP Control。

这里有两种解最佳策略的方法，一种是Policy iteration，一种是value iteration。这两个方法都是model-based的。

policy iteration:

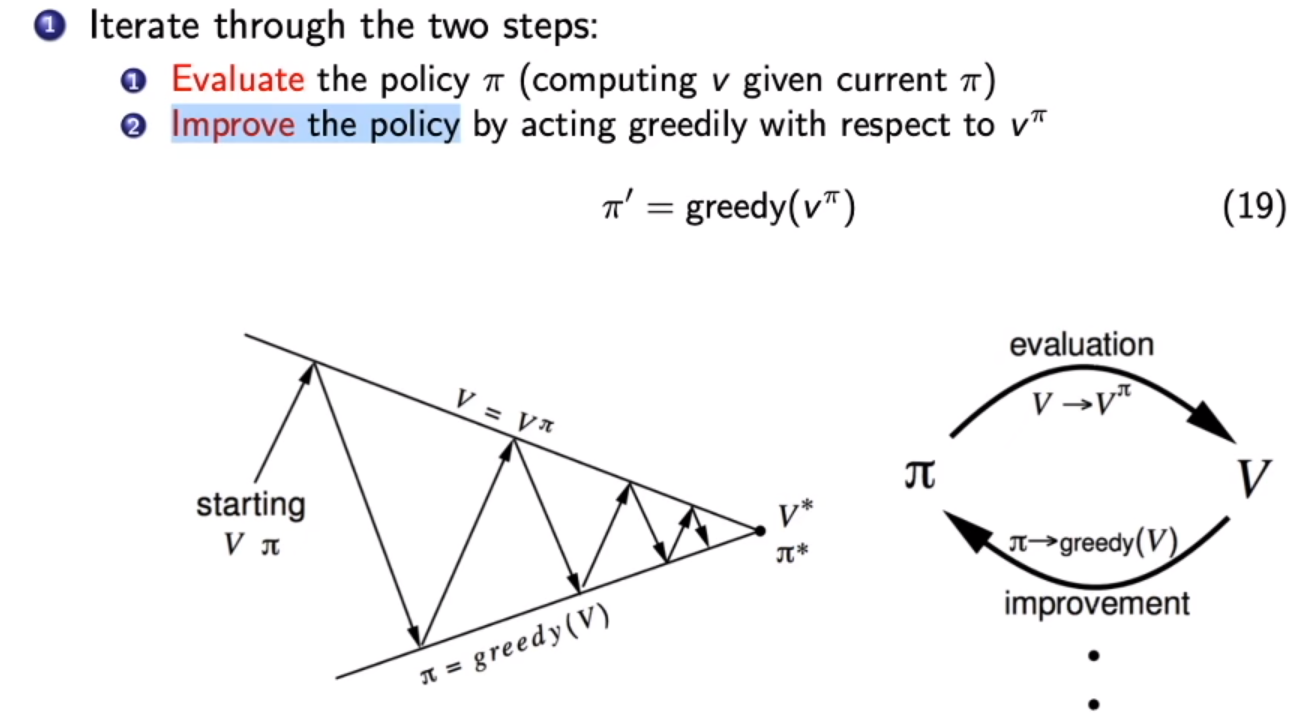
随机选择一个策略作为初始值。
Policy Evaluation：通过现有的策略π计算状态价值v。
Policy Improvement：计算当前最好的Action，更新策略$π(s) = argmax_a \sum_{s’,r}(r+\gamma V(s’))$。
不断循环第二和第三步。

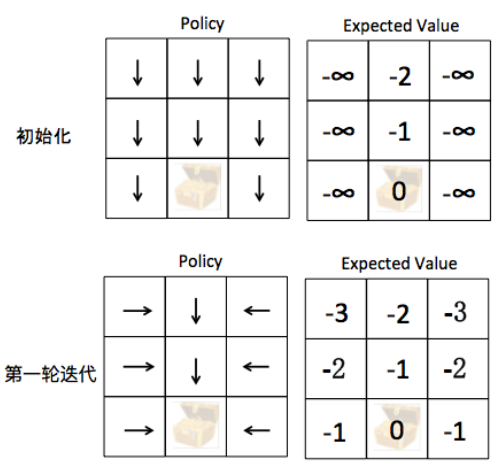
策略评估会评估从上次策略改进中获得的贪心策略的价值函数 V。另一方面，策略改进通过使每个状态的 V 值最大化的动作来更新策略。更新方程以贝尔曼方程为基础。它不断迭代直到收敛。

优化过后，贝尔曼最优等式（Bellman Optimality Equation）满足：
$$
v^{π}(s) = \max_{a \in A} q^π (s,a)
$$
之前的两条公式变为：
$$
v^*(s) = \max_aR(s,a) + \gamma \sum_{s’ \in S} P(s’|s ,a)v^*(s’)
$$

$$
q^* (s,a) = R(s,a) + \gamma \sum_{s’ \in S} P(s’|s ,a) \max_{a’} q^*(s’,a’)
$$

Q-learning就是基于贝尔曼最优等式实现的。

def policy_iteration(env, gamma = 1.0):
    """ Policy-Iteration algorithm """
    policy = np.random.choice(env.env.nA, size=(env.env.nS))  # initialize a random policy
    max_iterations = 200000
    gamma = 1.0
    for i in range(max_iterations):
        old_policy_v = compute_policy_v(env, policy, gamma)
        new_policy = extract_policy(old_policy_v, gamma)
        if (np.all(policy == new_policy)):
            print ('Policy-Iteration converged at step %d.' %(i+1))
            break
        policy = new_policy
    return policy

Value Iteration:

在Policy Iteration中
- 第一步 Policy Evaluation：一直迭代至收敛，获得准确的V(s)
- 第二步 Policy Improvement：根据准确的V(s)，求解最好的Action
对比之下，在Value Iteration中
- 第一步 “Policy Eval”：迭代只做一步，获得不太准确的V(s)
- 第二步 “Policy Improvement”：根据不太准确的V(s)，求解最好的Action

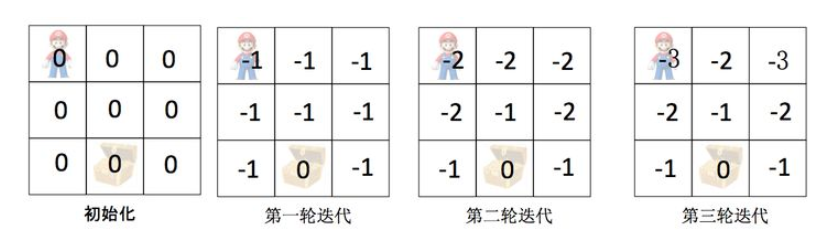
Value Iteration的迭代出optimal value function后只做一次policy update，即：循环（对于当前状态每个可能的action，都做一次value evaluation，然后取最大的value，作为当前状态的价值），直到收敛。最后，按照最优价值的转移方向更新一次策略。

这里把贝尔曼最优等式拿进来，寻找最佳的Value-Funciton，没有Policy Function在里面。
$$
v^*(s) \leftarrow \max_{a \in A}(R(s,a) + \gamma \sum_{s’ \in S} P(s’|s ,a)v^*(s’))
$$

def value_iteration(env, gamma = 1.0):
    """ Value-iteration algorithm """
    v = np.zeros(env.env.nS)  # initialize value-function
    max_iterations = 100000
    eps = 1e-20
    for i in range(max_iterations):
        prev_v = np.copy(v)
        for s in range(env.env.nS):
            q_sa = [sum([p*(r + gamma * prev_v[s_]) for p, s_, r, _ in env.env.P[s][a]]) for a in range(env.env.nA)] 
            v[s] = max(q_sa)
        if (np.sum(np.fabs(prev_v - v)) <= eps):
            print ('Value-iteration converged at iteration# %d.' %(i+1))
            break
    return v

Model-free Prediction and Control

Model-free下的价值估计

Model-free相对于model-based的不同在于是否知道MDP。而现实中大部分MDP都没有现成的模型可以用，所以我们只能采用Model-free的方法。

MDP已知：奖励函数R和转移矩阵P都可以为agent所知。所有agent才能通过Policy Iteration和Policy Iteration来寻找最佳策略。

在Model-free RL中，我们并没有直接获取转移状态和奖励函数，我们让agent跟环境进行交互，采集很多轨迹数据，agent需要从这些轨迹中获取信息，改进策略，以获得更多奖励。

当我们给定策略的时候，在没有给MDP转移模型的情况如何估计一个状态的价值？有两种常见的方法。一种是蒙泰卡罗（Monte Carlo policy evalution），一种是时序差分学习（Temporal Difference）

Monte-Carlo Policy Evaluation

蒙泰卡罗算法的做法是直接在某状态开始直接收集多条轨迹的数据，得到多个价值，然后把所有的价值平均起来得到该状态的价值$V_t(s)$，可以说随机的数量足够多，那么$V_t(s)$就会接近真实的价值。但这个算法的限制是只能用在有终止的马尔科夫决策过程。相对于动态规划（DP）来说，这是一个model-free的算法，而且只更新轨迹上的数据，速度较快。特点是需要跑完一个episode才能更新一次。
$$
v(S_t) \leftarrow v(S_t) + \alpha(G_{i,t} - v(S_t))
$$

Temporal-Difference（TD）Learning

这是一个介于MC和DP之间的方法。这既可以用于Model-free，也能在一个episode不完整的情况下实现更新，一个step就能更新一次，每次只更新一点。
$$
v(S_t) \leftarrow v(S_t) + \alpha(R_{t+1} + \gamma v(S_{t+1}) - v(S_t))
$$
这个算法可以拓展到2-step TD，3-step TD等等，每两个或三个step或更多step更新一次。当这个步数为无穷时，TD算法就可以转变为MC算法，这就是它们的联系。

各种算法直接的区别

对于动态规划，需要考虑到所有支路的情况，取一个期望。

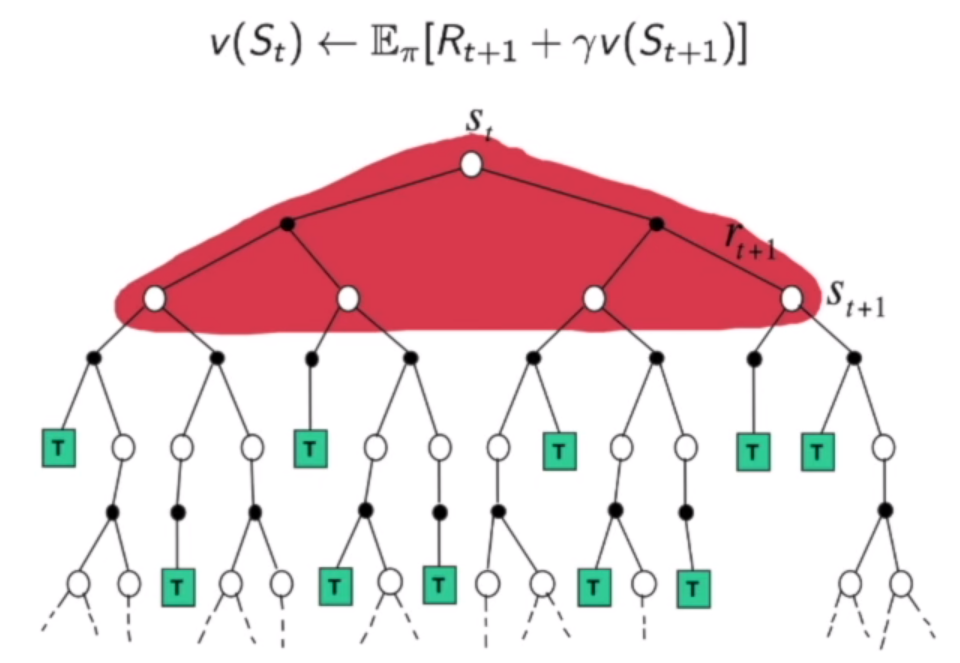
对于MC，我们每次只取一条路径来进行更新，期望通过多条路径的更新达到和期望一样的效果。

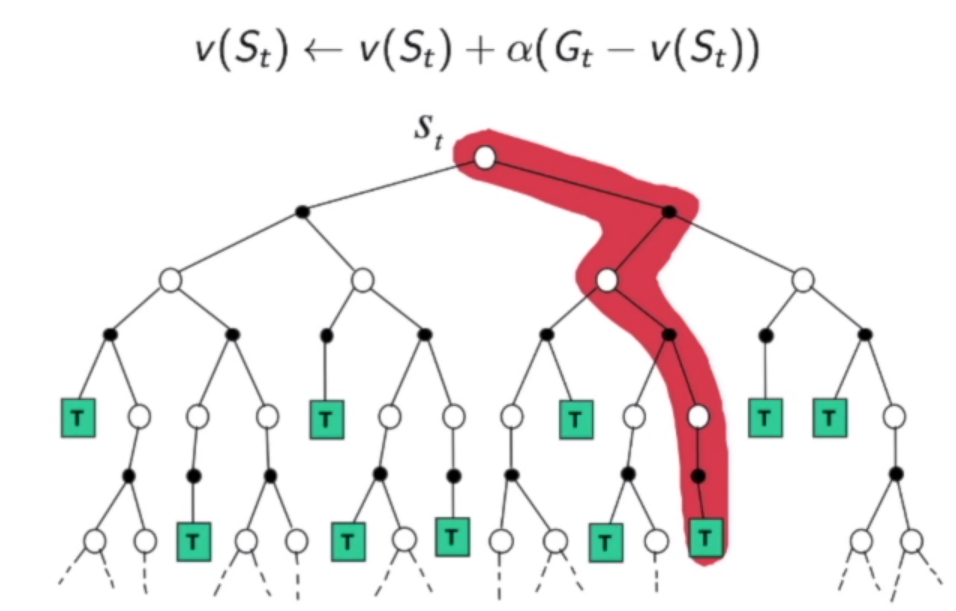
对于TD，每次还是走一条路径，一个step就更新一次。

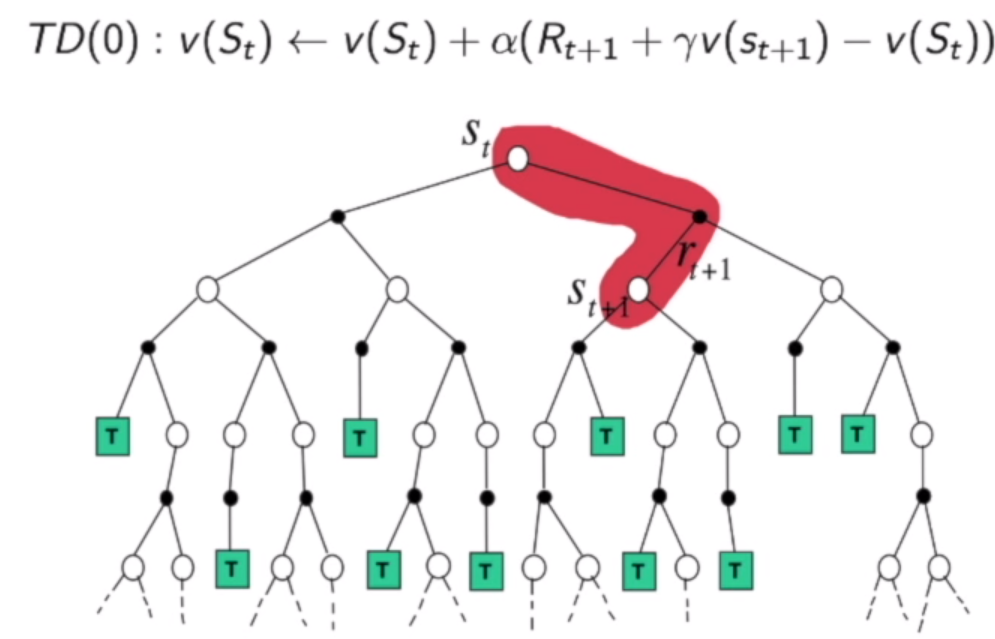
model-free下的策略更新

通常我们希望每个状态都能得到充分的更新，因此我们需要尽可能采样到比较多的状态。通过MC采样的方法我们需要采样尽可能多的轨迹，然后更新一个Q表格。同样我们用TD可以保证每个step进行更新，不用等episode结束。

我们需要保证算法有足够多的探索，因此我们在刚开始迭代的时候让算法有较大的概率随机采取action，而不是按照greedy也就是动作价值最大的策略，在后面再把这个概率降下来。

Sarsa

更新公式
$$
Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha [R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_{t},A_t)]
$$
其中α是学习率，我们每一个step需要更新Q表格中的一个值，更新完后使用greedy的策略进行探索，也有一定的概率随机探索，这是基于离散或有限状态的方法，是表格型的方法，没有用到神经网络。

# 学习方法，也就是更新Q-table的方法，采用Sarsa算法来更新Q表格
def learn(self, obs, action, reward, next_obs, next_action, done):
    """ on-policy
        obs: 交互前的obs, s_t
        action: 本次交互选择的action, a_t
        reward: 本次动作获得的奖励r
        next_obs: 本次交互后的obs, s_t+1
        next_action: 根据当前Q表格, 针对next_obs会选择的动作, a_t+1
        done: episode是否结束
    """
    predict_Q = self.Q[obs, action]
    if done:
        target_Q = reward  # 没有下一个状态了
    else:
        target_Q = reward + self.gamma * self.Q[next_obs,
                                                next_action]  # Sarsa
    self.Q[obs, action] += self.lr * (target_Q - predict_Q)  # 修正q

on-policy和off-policy

上面的算法Sarsa是一种on-policy的算法，也就是说探索和决策都采用同一种策略，而off-policy的算法是探索和决策采用不同的策略，这样我们在探索的时候就能使用更为激进的手段收集更多的数据，然后交给策略进行学习，这样也能比较有效利用到之前采集的数据。下面就讲一下off-policy中的Q-learning。

Q-learning

更新公式：
$$
Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha [R_{t+1} + \gamma \max_a Q(S_{t+1},a) - Q(S_{t},A_t)]
$$
可以看到，和Sarsa不同的地方在于我们没有用到第二个action，也就是说，我们无需知道下一个状态之后agent需要采取的动作。我们只需要从下一个状态采取的所有动作中选取动作价值最大的action的值来进行更新。因此更新用的第二个action和探索用的第二个action无关，这就是off-policy。Q-Learning的另一个特点是一个动作价值不会被隔壁的动作价值所影响，只取决于隔壁最大的动作价值。除了价值更新方法的不同，探索的策略依旧和Sarsa相同，这样Q-learning采取的策略就会比Sarsa激进得多。往往Q-learning会学习到最佳的策略。

def learn(self, obs, action, reward, next_obs, done):
        """ off-policy
            obs: 交互前的obs, s_t
            action: 本次交互选择的action, a_t
            reward: 本次动作获得的奖励r
            next_obs: 本次交互后的obs, s_t+1
            done: episode是否结束
        """
        predict_Q = self.Q[obs, action]
        if done:
            target_Q = reward  # 没有下一个状态了
        else:
            target_Q = reward + self.gamma * np.max(
                self.Q[next_obs, :])  # Q-learning
        self.Q[obs, action] += self.lr * (target_Q - predict_Q)  # 修正q