参考视频:https://www.bilibili.com/video/BV1yv411i7xd
代码下载:https://github.com/PaddlePaddle/PARL
可以先阅读我的文章《强化学习概述》,重复的内容不再叙述。代码主要参考强化学习算法框架库:PARL
资料推荐
书籍:《Reinforcement Learning: An Introduction》
视频:David Silver经典强化学习公开课、UC Berkeley CS285、斯坦福CS234
经典论文:
前沿研究方向:Model-base RL、Hierarchical RL、Multi Agent RL、Meta Learning。
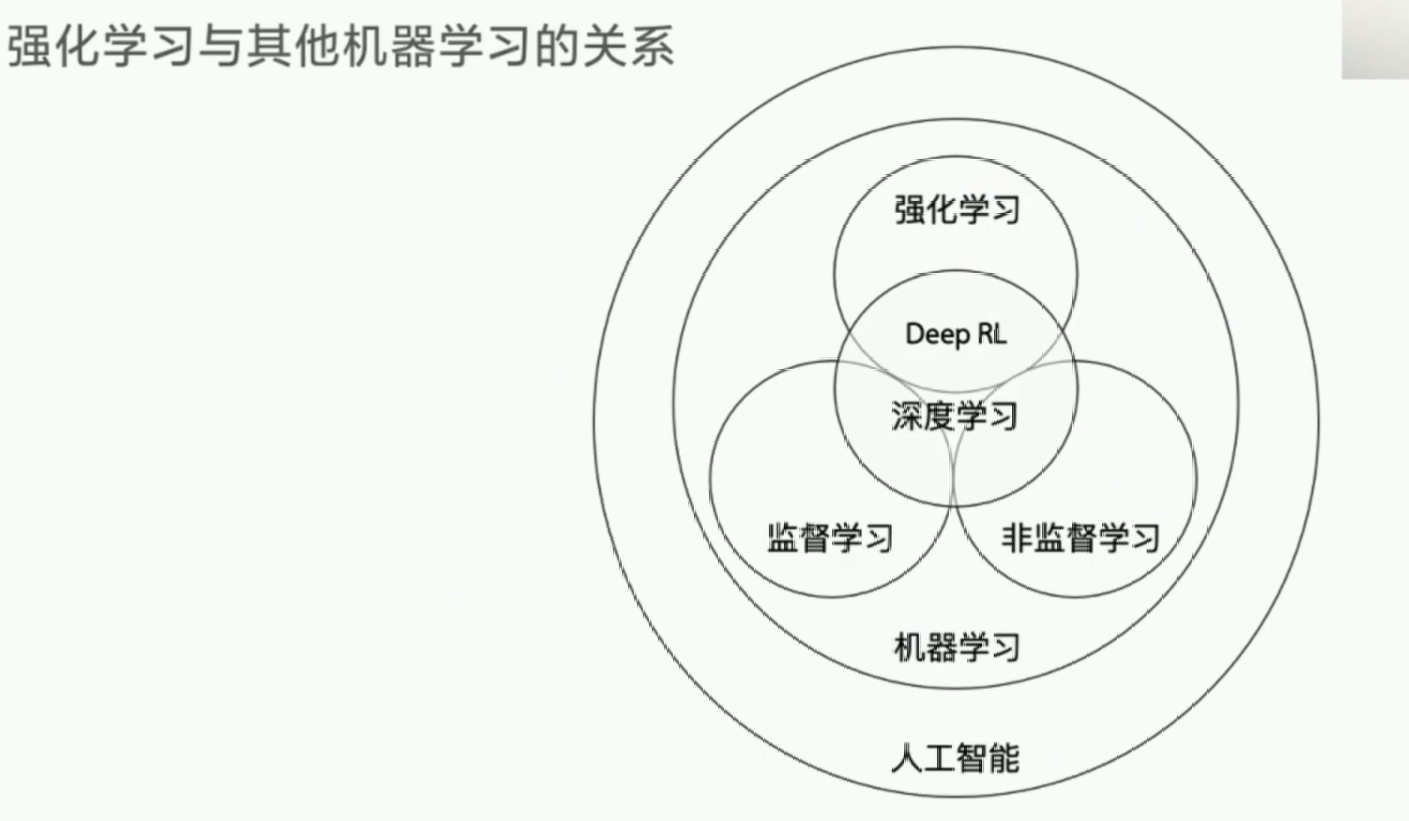
序章
Agent学习的两种方案
一种是基于价值(value-based),一种是基于策略(policy-based)
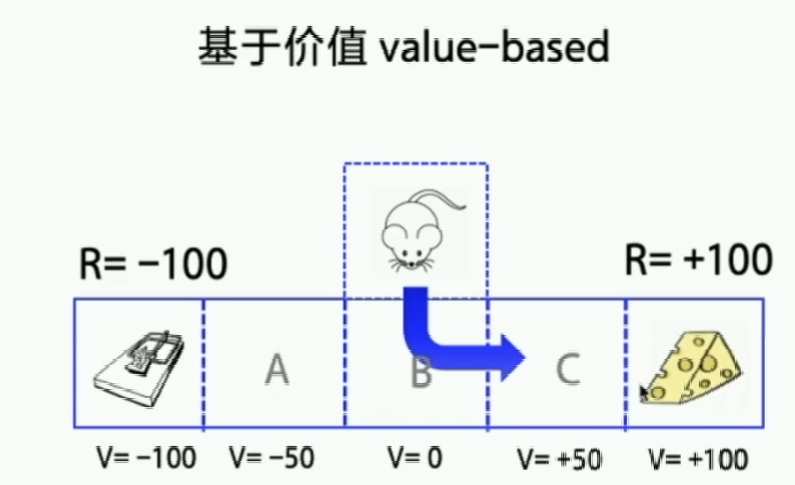
基于价值:我们给每一个状态都赋予一个“价值”的概念,例如上图C状态的价值大于A状态,也就是往C走离奖励更近。我们的做法是让Agent总是往价值高的地方移动,这样就能找出一个最优的策略。一旦函数优化到最优了,相同的输入永远是同一个输出。
代表方法:Sarsa、Q-learning、DQN。

基于策略:我们直接让一条策略走到底,然后用最后的reward来判断策略是好是坏。好的策略能在以后的行为中获得更高的触发几率。由于输出的是几率,因此同样的输入会获得不同的输出,随机性更强。
代表方法:Policy Gradient。
RL概览分类
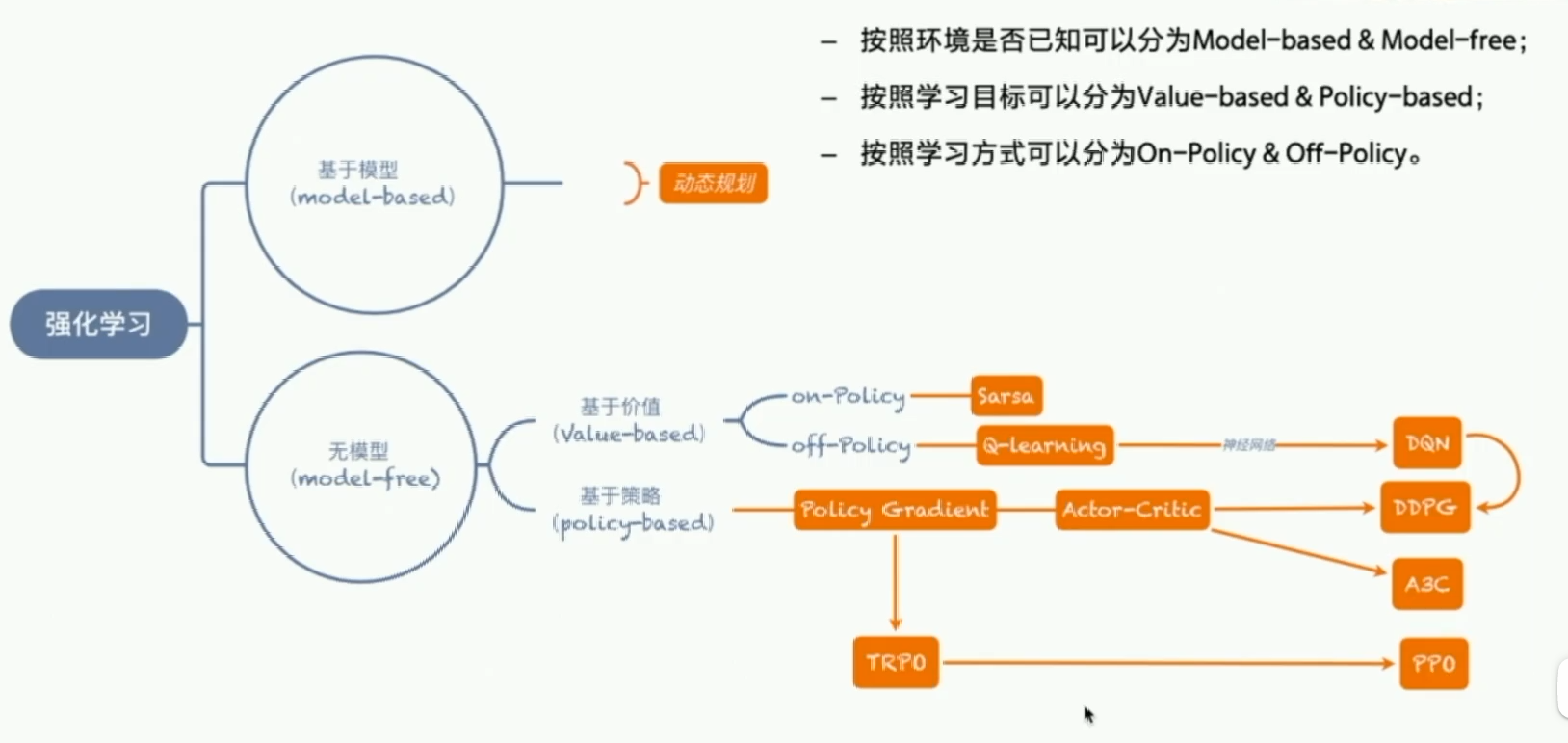
强化学习分为无模型(model-free)和基于模型(model-based),无模型的研究会更加热门,上面的两种方案都是无模型的分类。
Model-free: 不需要知道状态之间的转移概率(transition probability)。
Model-based: 需要知道状态之间的转移概率。
而在Model-free中又有三种分类:
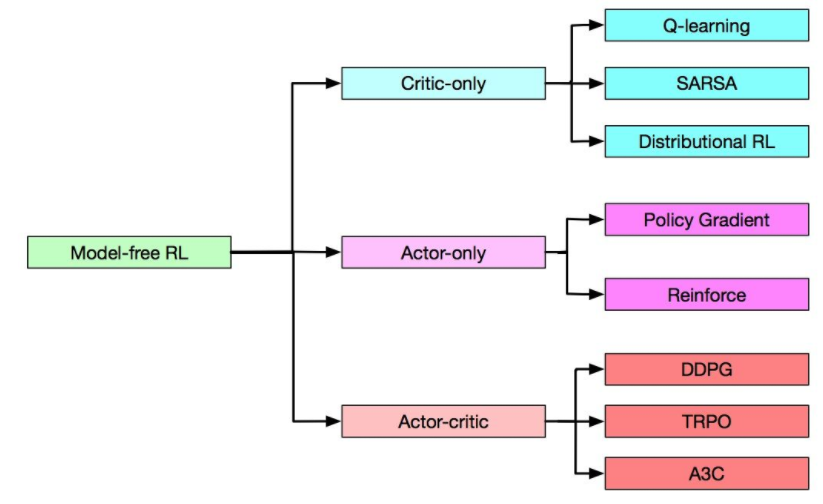
算法库
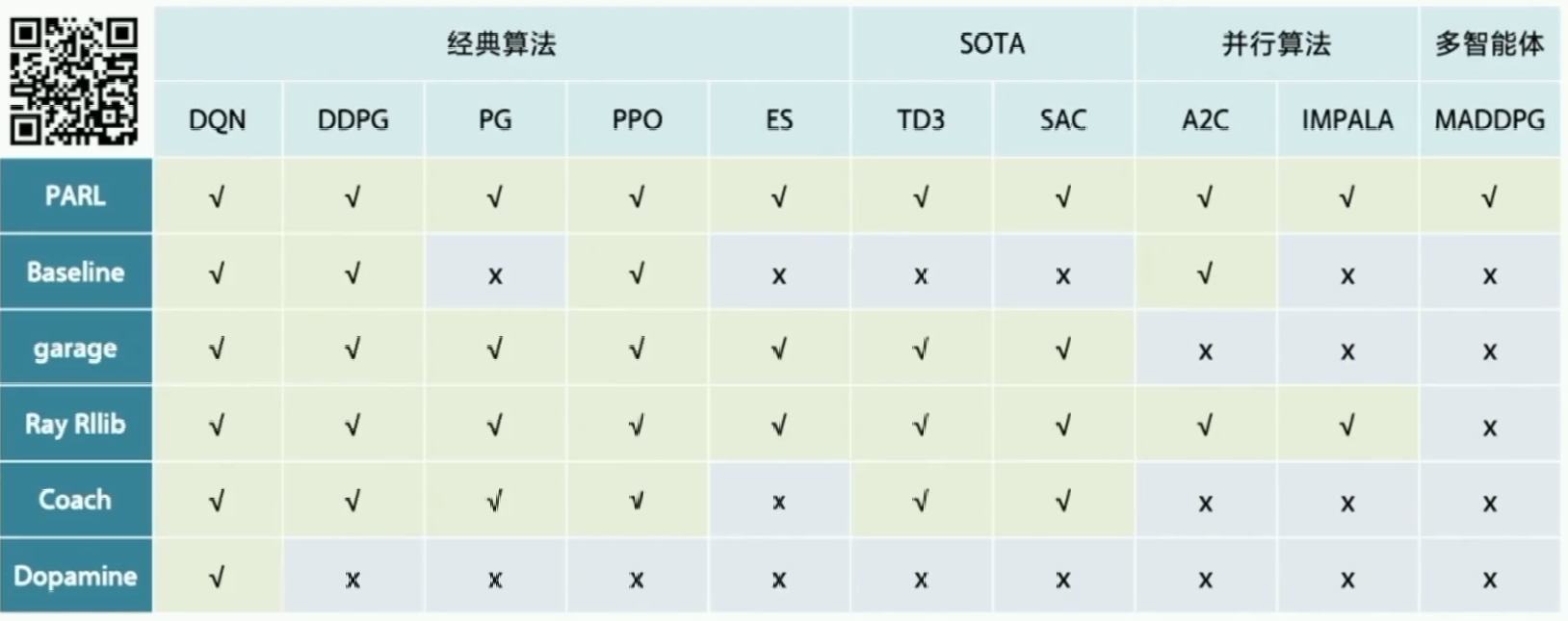
这里我们使用强化学习算法框架库:PARL。这里涵盖了很多的经典算法,又能复现一些最新的流行算法。看代码的学习方式,也是最快上手的学习方式。直接扫左上角二维码来学习。其中多智能体是一个热门的研究方向,被认为更接近人类社会的交互形式。
RL编程实践:GYM
前面的是和算法相关的库。另外一类是和环境相关的库。GYM是学术界比较喜欢的环境库。环境分为离散控制场景和连续控制场景,离散控制是输出只有有限个量,例如控制方向时只有向左向右,一般使用atari环境评估。连续控制是输出是一个连续的量,例如机械臂旋转的角度,一般使用mujoco环境来评估。

环境安装
在安装了python环境的前提下,打开cmd,输入以下命令:
pip install paddlepaddle==1.6.3 # 网络超时加上-i https://pypi.tuna.tsinghua.edu.cn/simple,安装GPU版本要用paddlepaddle-gpu
pip install parl==1.3.1 #如果安装不成功,在install后加上--user
pip install gym程序示例及PARL的优势

import gym
from gridworld import CliffWalkingWapper
import turtle
# 创建环境
env = gym.make("CliffWalking-v0")
# 绘制一个图形界面,不写这一行只有文字界面
env = CliffWalkingWapper(env)
# 重置界面,开始新的一轮
env.reset()
# 展示界面
env.render()
# 跟环境交互一步,如果有返回值第一个是纵坐标,第二个是reward,第三个是一轮是否结束
# step(1)是往右走,step(2)是往下走,step(3)是向左走
env.step(0)
env.render()
# 让程序运行结束后界面不立刻关闭
turtle.exitonclick()PARL对框架库做了很好的抽象,所有的算法几乎都集中于Model,Algorithm,Agent三个类。其中Algoritm已经实现了核心的部分,另外两部分开发者可以很方便实现订制。在上面下载的PARL中,有许多算法的Example。

从上面随便找一个example,然后对model和Agent文件做一定修改,就可以移植到新的应用场景中。
PARL的工业应用能力很强。只需要加两行代码,就可以把单机训练变成多机训练。PARL的并行能力很强,和Python不同,真正做到多线程运行,节省大量时间
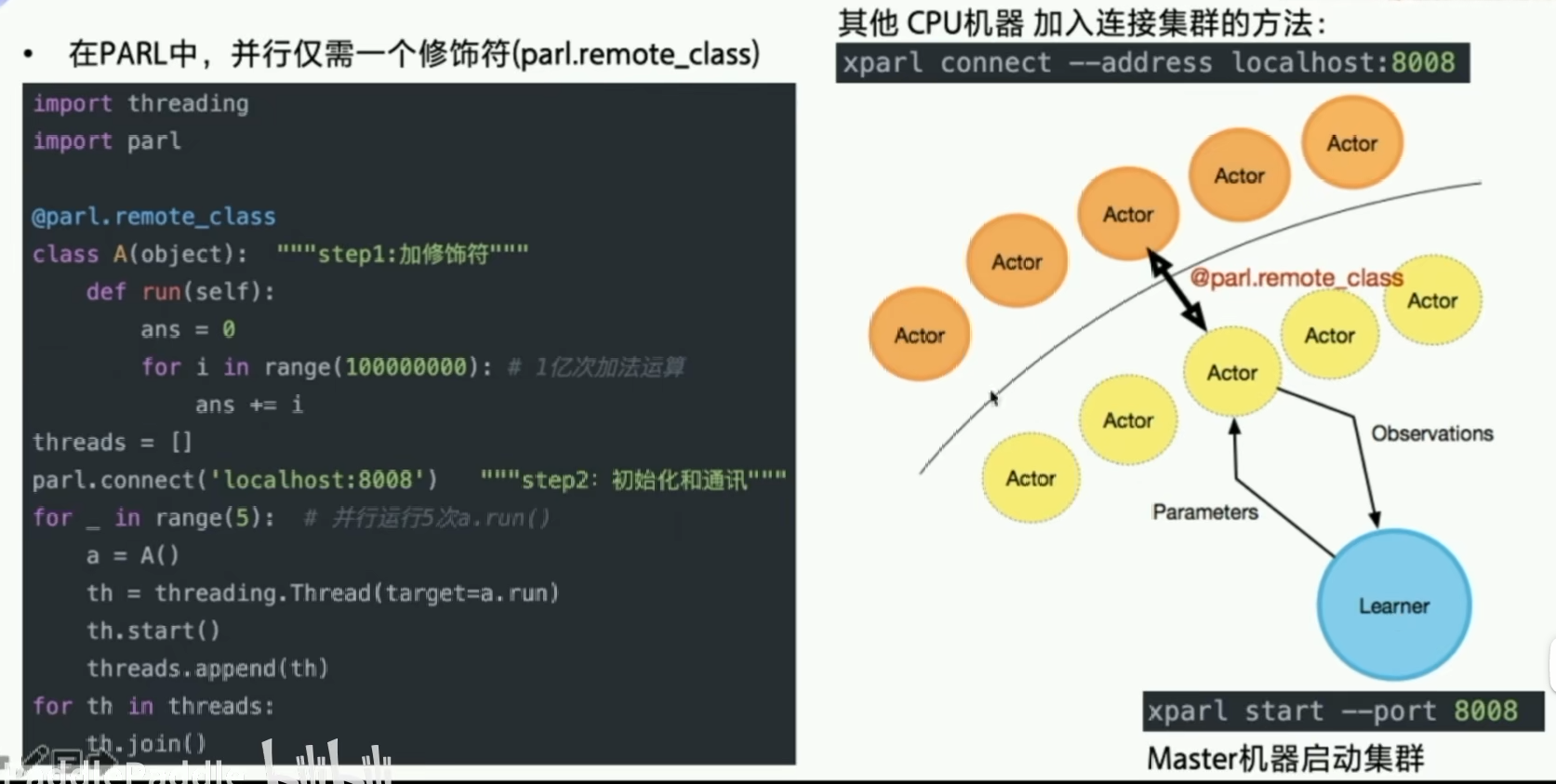
配置好环境后,直接运行QuickStart里面的程序,看看是否成功,此处本人没有运行成功,报错信息如下:
C:\Python39\lib\site-packages\parl\remote\communication.py:38: FutureWarning: 'pyarrow.default_serialization_context' is deprecated as of 2.0.0 and will be removed in a future version. Use pickle or the pyarrow IPC functionality instead.
context = pyarrow.default_serialization_context()
W0718 17:57:30.795331 4240 device_context.cc:404] Please NOTE: device: 0, GPU Compute Capability: 6.1, Driver API Version: 11.1, Runtime API Version: 10.2
[07-18 17:57:30 MainThread @train.py:73] obs_dim 4, act_dim 2
W0718 17:57:30.798295 4240 dynamic_loader.cc:238] Note: [Recommend] copy cudnn into CUDA installation directory.
For instance, download cudnn-10.0-windows10-x64-v7.6.5.32.zip from NVIDIA's official website,
then, unzip it and copy it into C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v10.0
You should do this according to your CUDA installation directory and CUDNN version.安装CUDNN依旧测试失败,如果有人知道缘由,请私聊。
基于表格型方法求解RL
强化学习MDP四元组
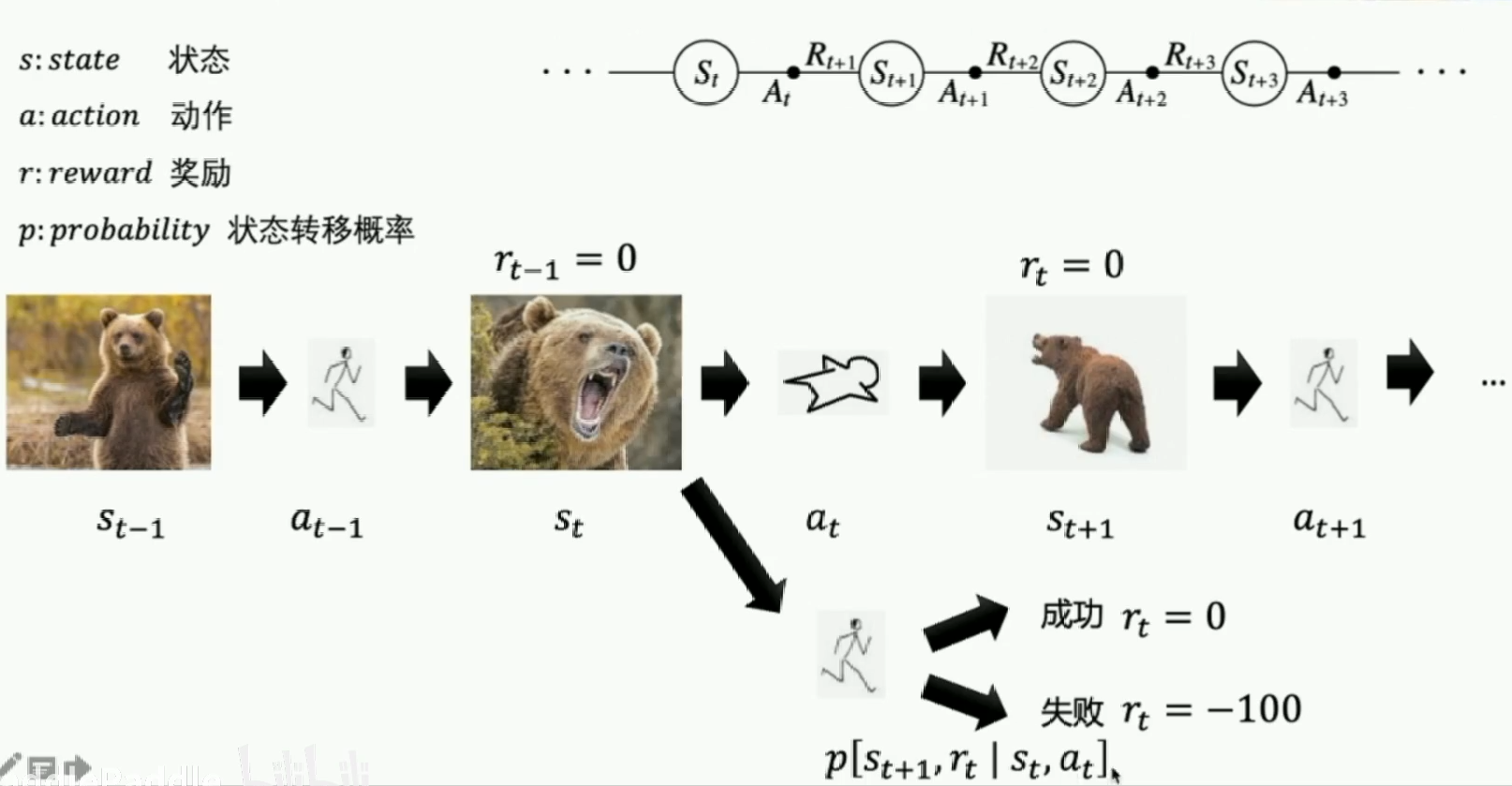
这就是强化学习MDP四元组。我们用状态转移概率表述:在$s_t$状态选择$a_t$的动作转移到$s_{t+1}$而且拿到奖励$r_t$的概率。这样的决策过程是马尔科夫决策过程(MDP)。这是一个序列决策的经典表达方式。
状态转移和序列决策
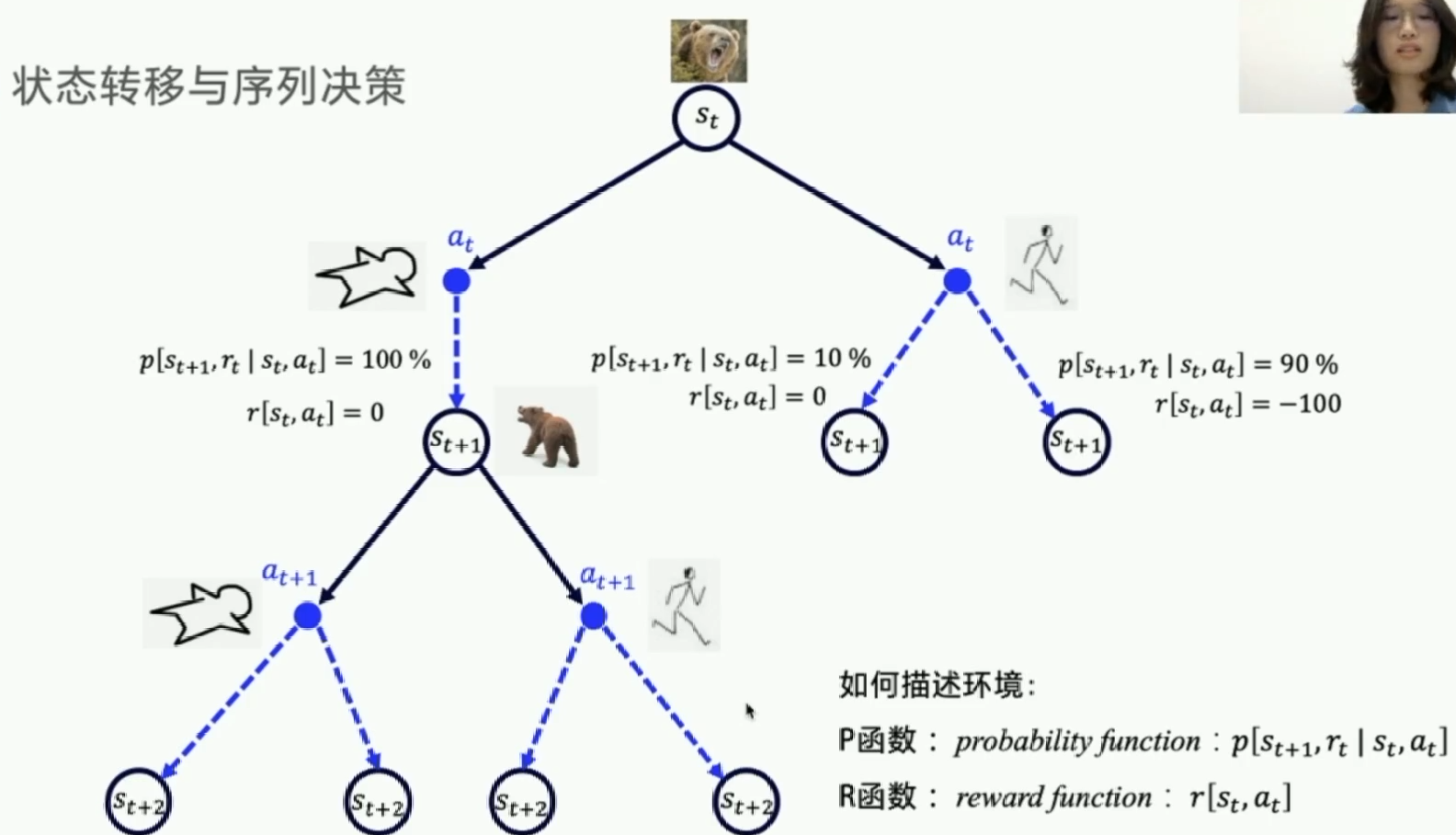
每次我们只能走其中的一条完整通路,这就是一个观察状态和执行决策不断循环的过程。每次我们都用两个函数描述环境。一个是Probability Function(P函数),反映了环境的随机性。一个状态如果必然转移到下一个特定的状态,那么状态转移概率是100%。如果有多种可能的情况,每个的状态转移概率在0到100%之间。和状态转移概率成对的是Reward Function(R函数),描述了环境的好坏。P函数和R函数已知,则称这个环境已知,也称为Model-based。如果这些条件已知,那么我们就可以用动态规划来寻找最优策略。但这里我们不讲动态规划。
这里我们针对的是在环境未知的情况下的解决方法,因为在实际问题中的状态转移概率往往是未知的。对于P函数和R函数未知的状况我们称为Model-free。
Q表格
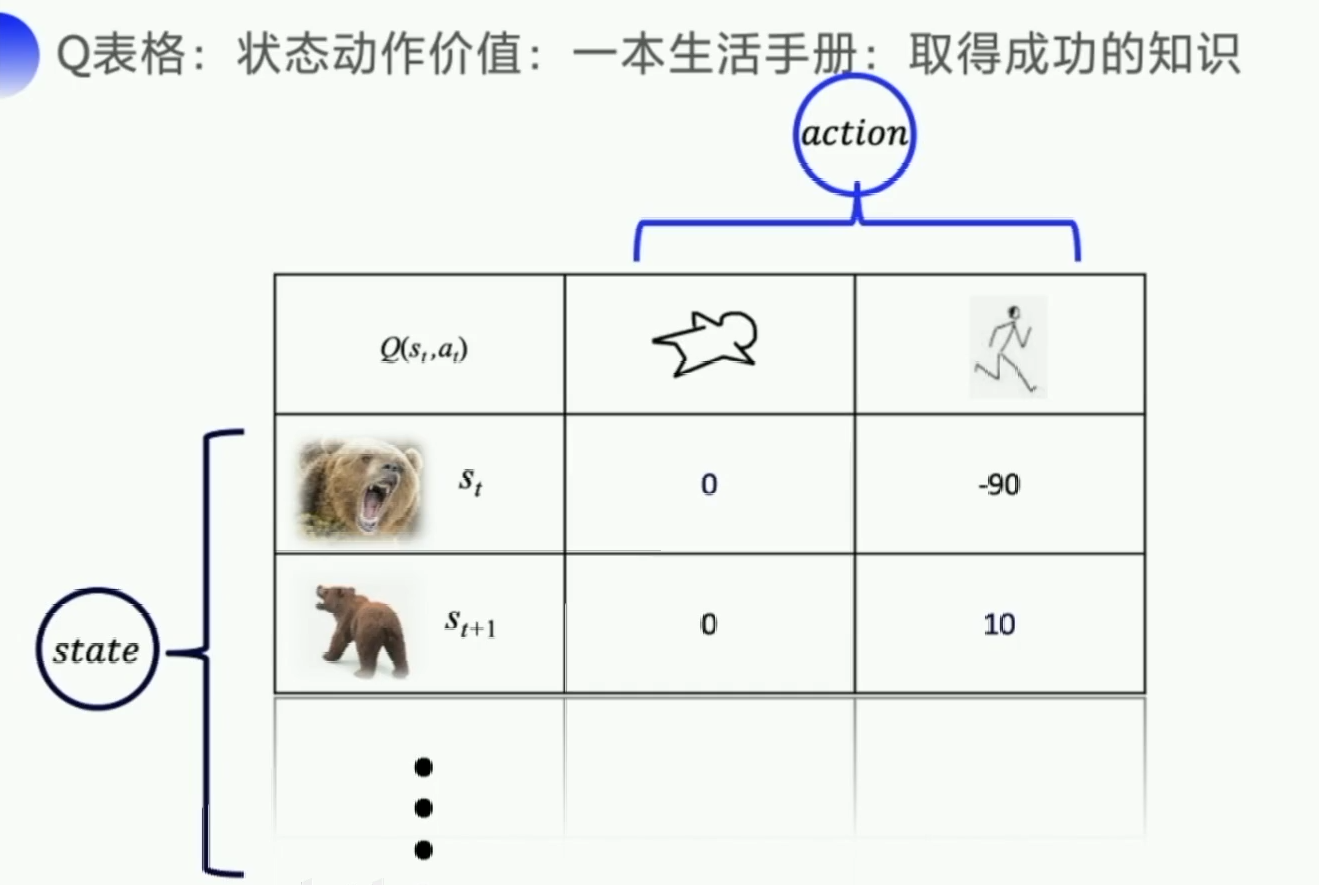
Q表格指导每一个Step的动作选择,目标导向是未来的总收益。由于收益往往具有延迟,因此未来的总收益才能代表当前动作选择的价值。但是由于前面的动作对越往后的状态影响越小,因此我们需要引入衰减因子。
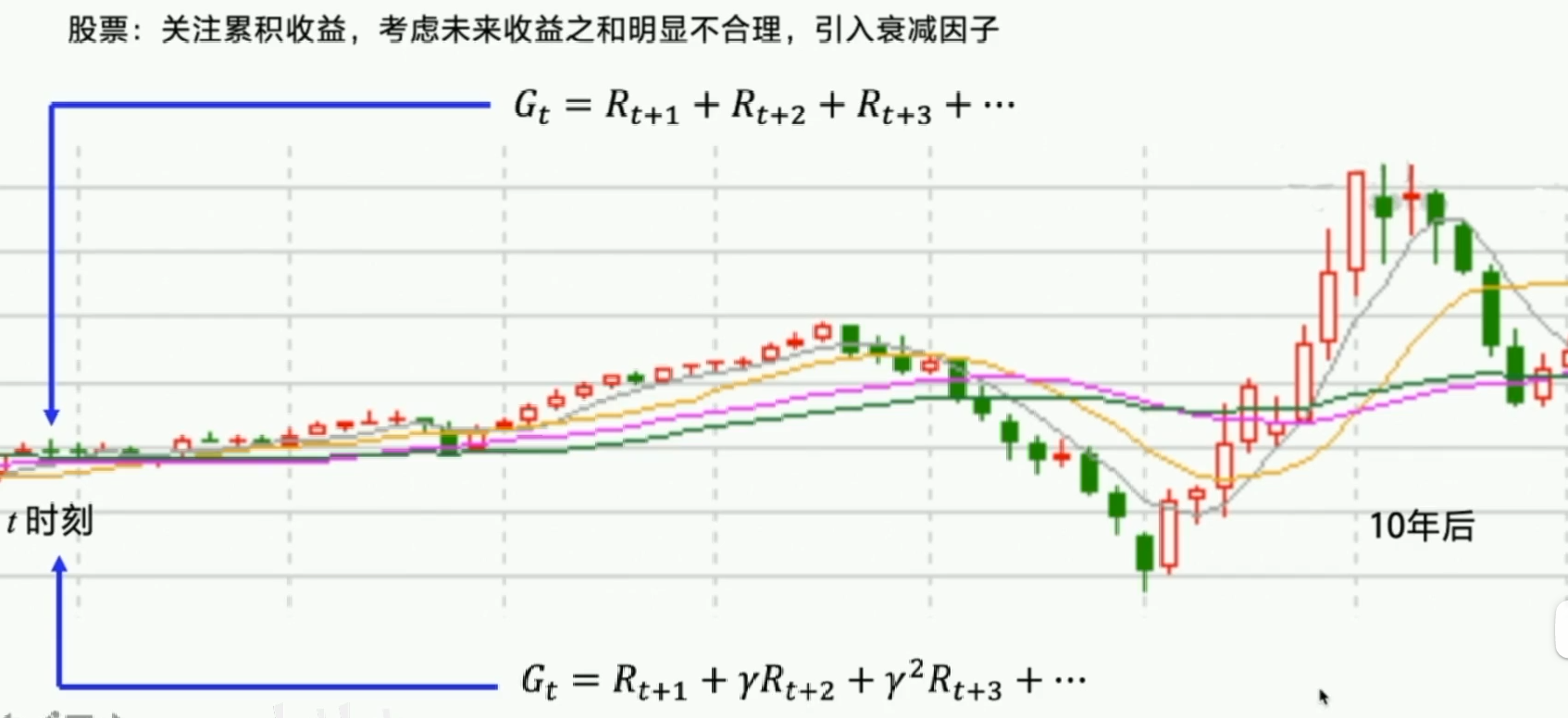
强化的概念是我们可以用下一个状态的价值更新现在状态的价值。因此我们每一个Step都可以更新Q表格,这是一种时序差分的更新方法。
时序差分(Temporal Difference)
推荐一个有意思的网站:https://cs.stanford.edu/people/karpathy/reinforcejs/gridworld_td.html
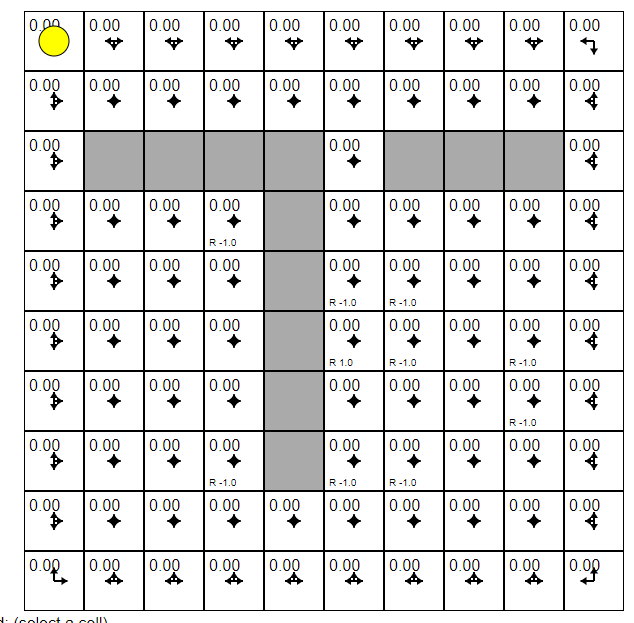
只有一个格子的reward为1,有很多格子reward为-1,随着小球的探索,有价值的格子也会把周围格子的分数拉高,形成一个整体的“评分体系”。只需要沿着分数增加的方向走一定能找到reward为1的点。

这就是一种时序差分的更新方法。
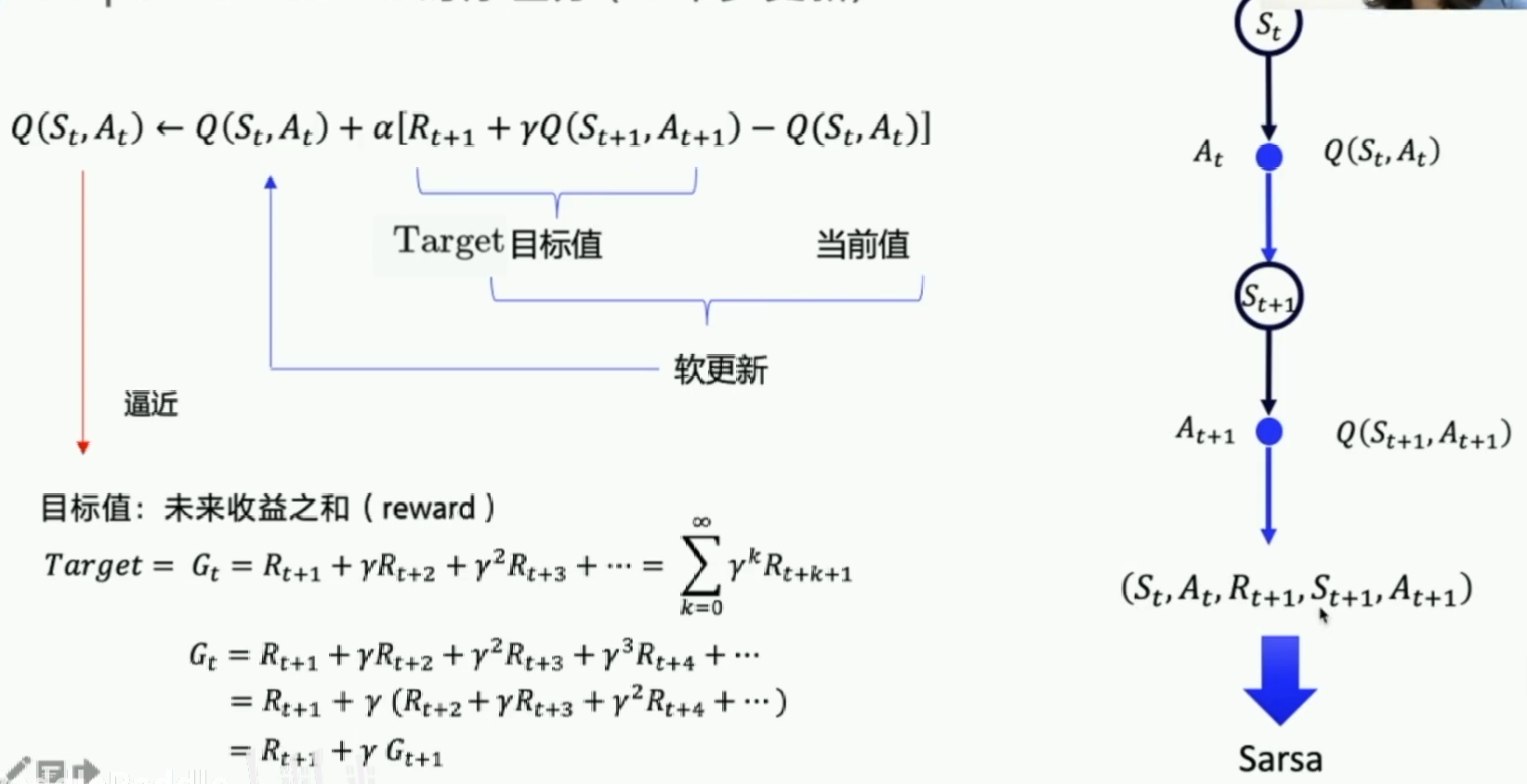
我们要让$Q(S_t,A_t)$逐步逼近理想的值,因此我们每次只更新一点点,α就是更新的速率。通过不断的更新我们可以让每一个状态的$G_t$都满足:
$$
G_t = R_{t+1} + \gamma G_{t+1}
$$
这就是Sarsa算法,命名方式是按照这五个值来进行计算。上面的格子的价值更新就是按照上面的公式来的。
Sarsa算法代码解析
Agent最重要的是实现两个功能,一个是根据算法选Action,第二个是学习Q表格。并且每一个step都包含这两步。
我们要另开一个agent.py文件,声明一个Agent类,Sample函数选择要输出Action,learn函数来更新Q。
class SarsaAgent(object):
def __init__(self,obs_n,act_n,learning_rate=0.01,gamma=0.9,e_greed=0.1):
self.act_n = act_n # 动作维度,有几个动作可选
self.lr = learning_rate # 学习率
self.gamma = gamma # reward的衰减率
self.epsilon = e_greed # 按一定概率随机选动作
self.Q = np.zeros((obs_n, act_n)) #生成一个矩阵作为Q表格,参数分别是状态的维度和动作维度,有多少格子就有多少状态
# 根据输入观察值,返回输出的Action对应的索引,带探索
def sample(self, obs):
if np.random.uniform(0, 1) < (1.0 - self.epsilon): #根据table的Q值选动作
action = self.predict(obs)
else:
action = np.random.choice(self.act_n) #有一定概率随机探索选取一个动作
return action
# 根据输入观察值,输出分数最高的一个动作值
def predict(self, obs):
Q_list = self.Q[obs, :]
maxQ = np.max(Q_list)
#where函数返回一个包含数组和数据类型的元组,取第一个才是数组
action_list = np.where(Q_list == maxQ)[0] # maxQ可能对应多个action
action = np.random.choice(action_list)
return action
# 学习方法,也就是更新Q-table的方法,采用Sarsa算法来更新Q表格
def learn(self, obs, action, reward, next_obs, next_action, done):
""" on-policy
obs: 交互前的obs, s_t
action: 本次交互选择的action, a_t
reward: 本次动作获得的奖励r
next_obs: 本次交互后的obs, s_t+1
next_action: 根据当前Q表格, 针对next_obs会选择的动作, a_t+1
done: episode是否结束
"""
predict_Q = self.Q[obs, action]
if done:
target_Q = reward # 没有下一个状态了
else:
target_Q = reward + self.gamma * self.Q[next_obs,
next_action] # Sarsa
self.Q[obs, action] += self.lr * (target_Q - predict_Q) # 修正q
# 保存Q表格
def save(self):
npy_file = './q_table.npy'
np.save(npy_file, self.Q)
print(npy_file + ' saved.')
# 读取Q表格
def restore(self, npy_file='./q_table.npy'):
self.Q = np.load(npy_file)
print(npy_file + ' loaded.')然后再开一个文件写我们的main函数:
import gym
from gridworld import CliffWalkingWapper, FrozenLakeWapper
from agent import SarsaAgent
import time
def run_episode(env, agent, render=False):
total_steps = 0 # 记录每个episode走了多少step
total_reward = 0
obs = env.reset() # 重置环境, 重新开一局(即开始新的一个episode)
action = agent.sample(obs) # 根据算法选择一个动作
while True:
next_obs, reward, done, _ = env.step(action) # 执行动作,action在0~3代表不同方向,并返回下一个状态
next_action = agent.sample(next_obs) # 根据算法选择下一个动作
# 训练 Sarsa 算法,更新Q表格
agent.learn(obs, action, reward, next_obs, next_action, done)
action = next_action # 把下一个动作更新为现在的动作
obs = next_obs # 把下一个状态更新为现在的状态
total_reward += reward
total_steps += 1 # 计算step数
if render:
env.render() #渲染新的一帧图形
if done:
break
return total_reward, total_steps
# 测试函数
def test_episode(env, agent):
total_reward = 0
obs = env.reset()
while True:
action = agent.predict(obs) # greedy
next_obs, reward, done, _ = env.step(action)
total_reward += reward
obs = next_obs
time.sleep(0.5)
env.render()
if done:
print('test reward = %.1f' % (total_reward))
break
def main():
# env = gym.make("FrozenLake-v0", is_slippery=False) # 0 left, 1 down, 2 right, 3 up
# env = FrozenLakeWapper(env)
env = gym.make("CliffWalking-v0") # 0 up, 1 right, 2 down, 3 left
# 创建一个图形界面
env = CliffWalkingWapper(env)
# 实例化agent
agent = SarsaAgent(
obs_n=env.observation_space.n,
act_n=env.action_space.n,
learning_rate=0.1,
gamma=0.9,
e_greed=0.1)
is_render = False
for episode in range(500):
ep_reward, ep_steps = run_episode(env, agent, is_render)
print('Episode %s: steps = %s , reward = %.1f' % (episode, ep_steps,
ep_reward))
# 每隔20个episode渲染一下看看效果
if episode % 20 == 0:
is_render = True
else:
is_render = False
# 训练结束,查看算法效果
test_episode(env, agent)
if __name__ == "__main__":
main()
生成图形环境的文件gridworld.py的代码如下:
import gym
import turtle
import numpy as np
# turtle tutorial : https://docs.python.org/3.3/library/turtle.html
def GridWorld(gridmap=None, is_slippery=False):
if gridmap is None:
gridmap = ['SFFF', 'FHFH', 'FFFH', 'HFFG']
env = gym.make("FrozenLake-v0", desc=gridmap, is_slippery=False)
env = FrozenLakeWapper(env)
return env
class FrozenLakeWapper(gym.Wrapper):
def __init__(self, env):
gym.Wrapper.__init__(self, env)
self.max_y = env.desc.shape[0]
self.max_x = env.desc.shape[1]
self.t = None
self.unit = 50
def draw_box(self, x, y, fillcolor='', line_color='gray'):
self.t.up()
self.t.goto(x * self.unit, y * self.unit)
self.t.color(line_color)
self.t.fillcolor(fillcolor)
self.t.setheading(90)
self.t.down()
self.t.begin_fill()
for _ in range(4):
self.t.forward(self.unit)
self.t.right(90)
self.t.end_fill()
def move_player(self, x, y):
self.t.up()
self.t.setheading(90)
self.t.fillcolor('red')
self.t.goto((x + 0.5) * self.unit, (y + 0.5) * self.unit)
def render(self):
if self.t == None:
self.t = turtle.Turtle()
self.wn = turtle.Screen()
self.wn.setup(self.unit * self.max_x + 100,
self.unit * self.max_y + 100)
self.wn.setworldcoordinates(0, 0, self.unit * self.max_x,
self.unit * self.max_y)
self.t.shape('circle')
self.t.width(2)
self.t.speed(0)
self.t.color('gray')
for i in range(self.desc.shape[0]):
for j in range(self.desc.shape[1]):
x = j
y = self.max_y - 1 - i
if self.desc[i][j] == b'S': # Start
self.draw_box(x, y, 'white')
elif self.desc[i][j] == b'F': # Frozen ice
self.draw_box(x, y, 'white')
elif self.desc[i][j] == b'G': # Goal
self.draw_box(x, y, 'yellow')
elif self.desc[i][j] == b'H': # Hole
self.draw_box(x, y, 'black')
else:
self.draw_box(x, y, 'white')
self.t.shape('turtle')
x_pos = self.s % self.max_x
y_pos = self.max_y - 1 - int(self.s / self.max_x)
self.move_player(x_pos, y_pos)
class CliffWalkingWapper(gym.Wrapper):
def __init__(self, env):
gym.Wrapper.__init__(self, env)
self.t = None
self.unit = 50
self.max_x = 12
self.max_y = 4
def draw_x_line(self, y, x0, x1, color='gray'):
assert x1 > x0
self.t.color(color)
self.t.setheading(0)
self.t.up()
self.t.goto(x0, y)
self.t.down()
self.t.forward(x1 - x0)
def draw_y_line(self, x, y0, y1, color='gray'):
assert y1 > y0
self.t.color(color)
self.t.setheading(90)
self.t.up()
self.t.goto(x, y0)
self.t.down()
self.t.forward(y1 - y0)
def draw_box(self, x, y, fillcolor='', line_color='gray'):
self.t.up()
self.t.goto(x * self.unit, y * self.unit)
self.t.color(line_color)
self.t.fillcolor(fillcolor)
self.t.setheading(90)
self.t.down()
self.t.begin_fill()
for i in range(4):
self.t.forward(self.unit)
self.t.right(90)
self.t.end_fill()
def move_player(self, x, y):
self.t.up()
self.t.setheading(90)
self.t.fillcolor('red')
self.t.goto((x + 0.5) * self.unit, (y + 0.5) * self.unit)
def render(self):
if self.t == None:
self.t = turtle.Turtle()
self.wn = turtle.Screen()
self.wn.setup(self.unit * self.max_x + 100,
self.unit * self.max_y + 100)
self.wn.setworldcoordinates(0, 0, self.unit * self.max_x,
self.unit * self.max_y)
self.t.shape('circle')
self.t.width(2)
self.t.speed(0)
self.t.color('gray')
for _ in range(2):
self.t.forward(self.max_x * self.unit)
self.t.left(90)
self.t.forward(self.max_y * self.unit)
self.t.left(90)
for i in range(1, self.max_y):
self.draw_x_line(
y=i * self.unit, x0=0, x1=self.max_x * self.unit)
for i in range(1, self.max_x):
self.draw_y_line(
x=i * self.unit, y0=0, y1=self.max_y * self.unit)
for i in range(1, self.max_x - 1):
self.draw_box(i, 0, 'black')
self.draw_box(self.max_x - 1, 0, 'yellow')
self.t.shape('turtle')
x_pos = self.s % self.max_x
y_pos = self.max_y - 1 - int(self.s / self.max_x)
self.move_player(x_pos, y_pos)
On-policy和Off-policy
On-policy: 探索环境使用的策略和要更新的策略是一个策略(SARSA)
Off-policy: 探索环境使用的策略和要更新的策略不是同一个策略(Q-learning)
上面我们学的SARSA是on-policy,优化的是实际执行的策略,因此只存在一种策略。off-policy在学习的过程中保留了两种不同的策略,一种是Target policy,使我们想要的最佳的目标策略。另一个是Behavior policy,是探索环境的策略,需要大胆探索所有可能的环境,然后交给目标策略去学习。而且交给目标策略的数据不需要$A_{t+1}$(也就是Sarsa最后一个a)。
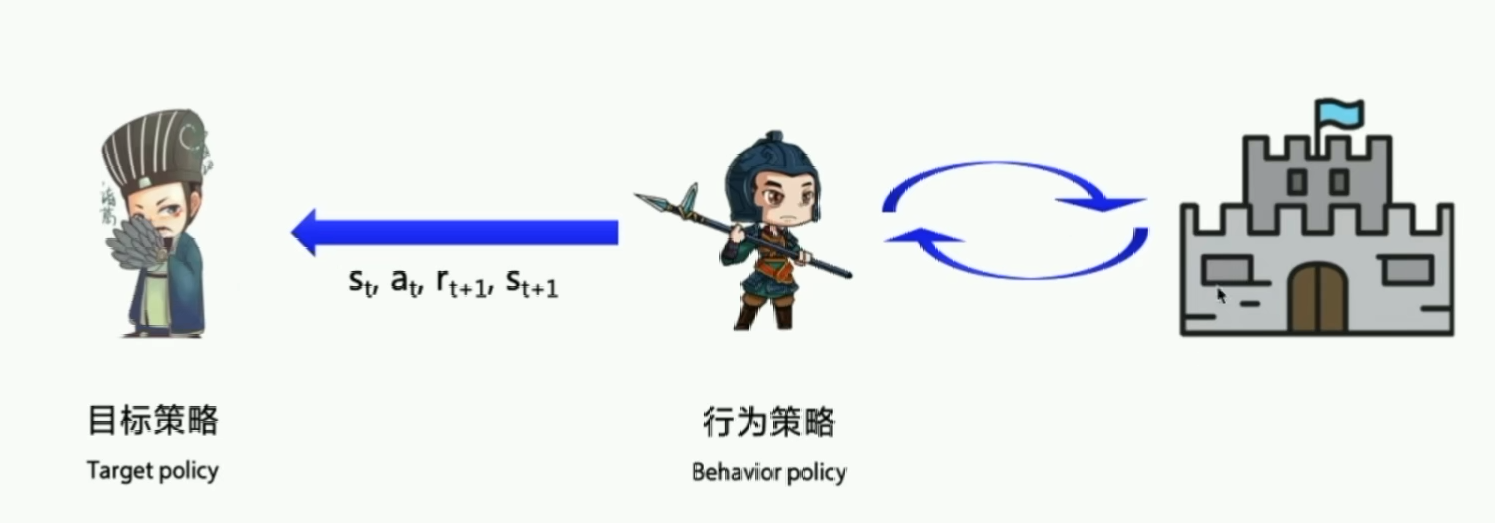
对比:

Q-learning

可以看到代码实现方面Q-learning和Sarsa类似,只是把初始action的选择也放到了循环当中,并且learn函数已经不用传入$A_{t+1}$了。
而在Agent类中,只有learn函数中的一行和Sarsa有区别,也就是Q表格的更新公式。
class QLearningAgent(object):
--snip--
# 学习方法,也就是更新Q-table的方法
def learn(self, obs, action, reward, next_obs, done):
""" off-policy
obs: 交互前的obs, s_t
action: 本次交互选择的action, a_t
reward: 本次动作获得的奖励r
next_obs: 本次交互后的obs, s_t+1
done: episode是否结束
"""
predict_Q = self.Q[obs, action]
if done:
target_Q = reward # 没有下一个状态了
else:
target_Q = reward + self.gamma * np.max(
self.Q[next_obs, :]) # Q-learning
self.Q[obs, action] += self.lr * (target_Q - predict_Q) # 修正q
--snip--也就是说,探索的策略没变,都是往高价值的格子方向探索并带有10%的探索几率。但是更新格子价值的时候,我们并不是根据探索的下一步来调整格子的价值,而是挑选周围全部可以达到的格子价值的最大值。因此,在Q-learning中,价值低的格子并不能影响周围格子的价值,只有价值高的格子才能影响周围格子的价值。
这和Sarsa不同,Sarsa下一步格子的价值都会影响到上一步格子,因此在reward为负数的格子周围那些格子的价值也为负数,因此agent会绕的远远地。而Q-learning,没有这个顾虑,因此agent直接就是最短路径拿到reward,因此total-reward会比Sarsa高。
总结
Sarsa的策略偏向于保守,既会趋利也会避害,即使探索不太完全也会里reward底的地方较远(防止随机走的时候掉进去),而Q-learning更具探索性,能找到一条最优的路径,但是探索的时候Behavior policy容易随机reward低点,但这不妨碍Target policy学习到更好的策略。
其中每走一步reward减1的设定是探索的关键点。由于没有探索到的格子价值为0,而探索到的无reward格子的价值往往为负数,agent会更趋向于探索没有探索过的格子。
那么Sarsa和Q-learning这两个经典的表格型算法和编程实现到此讲解完毕。
拓展

讲到这里,你应该已经了解两个算法的具体实现了,到多个环境中去跑算法观察现象吧!我们可以自定义格子世界,看看我们的算法是如何找到最优路径的。
同时,我也发现这两个算法都有一定的缺陷,就是没有办法跑黑块较多且较大的地图,这是由于战线过长中途又没有反馈,因此agent很难知道自己走的路线是对是错,我个人的想法是,往往这时候我们需要人为加入额外的reward来引导。

基于神经网络方法求解RL
关于神经网络的内容可以自行查看深度学习内容,或查看我的文章《李宏毅机器学习2021》https://tianjuewudi.gitee.io/2021/05/07/li-hong-yi-ji-qi-xue-xi-2021/。以及《Pytorch实战教学》。
当我们的强化学习(RL)碰到了深度学习(DL),我们就来到了深度强化学习(DRL)的领域。
表格法有很大的缺陷:
- 表格占用的内存空间巨大。
- 当表格极大时,查表效率低下。
- 只能表示有限个离散状态和动作。
现在我们需要更换工具了,我们可以用神经网络来代替表格法,我们可以用S和A作为神经网络的输入,由此输出价值Q。也可以输入S并输出多个Q,每个Q对应一个A。神经网络只需要储存有限的网络参数,我们的任务就是不断调整这些参数,使得输入输出符合我们的预期,而且状态可以泛化,相似的状态输出也差不多,不用像表格法一样需要重新训练。
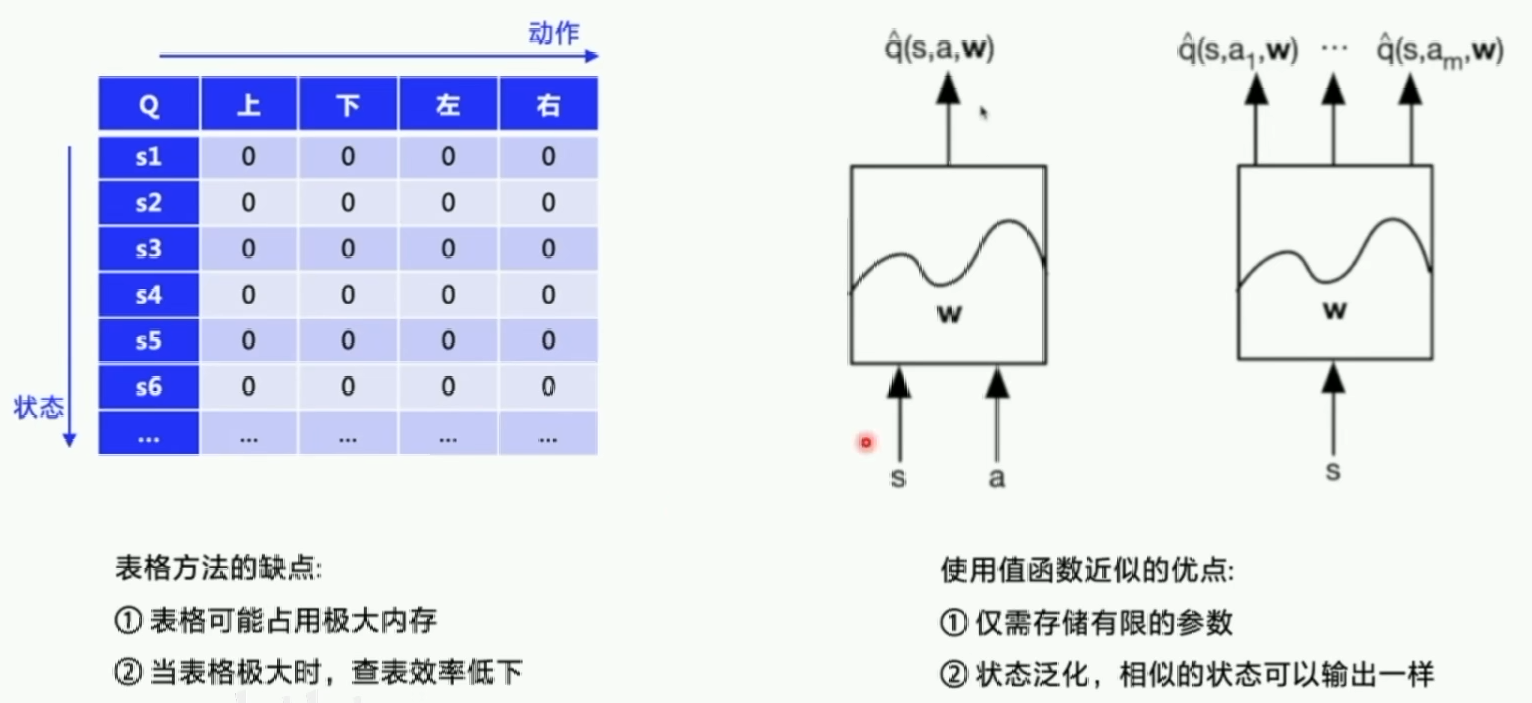
其中利用神经网络求解RL的经典算法是DQN。这是2015年发表在Nature上的论文。神经网络的输入是像素级别的图像,使用神经网络近似代替Q表格,49个游戏中有30个超越人类水平。
DQN

DQN的做法类似于Q-learning和神经网络的组合。首先神经网络的训练方法是监督学习,其中训练的样本就是输入状态变量,输出动作Action,我们通过Q-learning不断更新这些样本,然后送到神经网络中进行训练,期望拟合出一个和原来Q表格差不多的神经网络。
DQN提出了两个创新点使得其更有效率也更稳定。
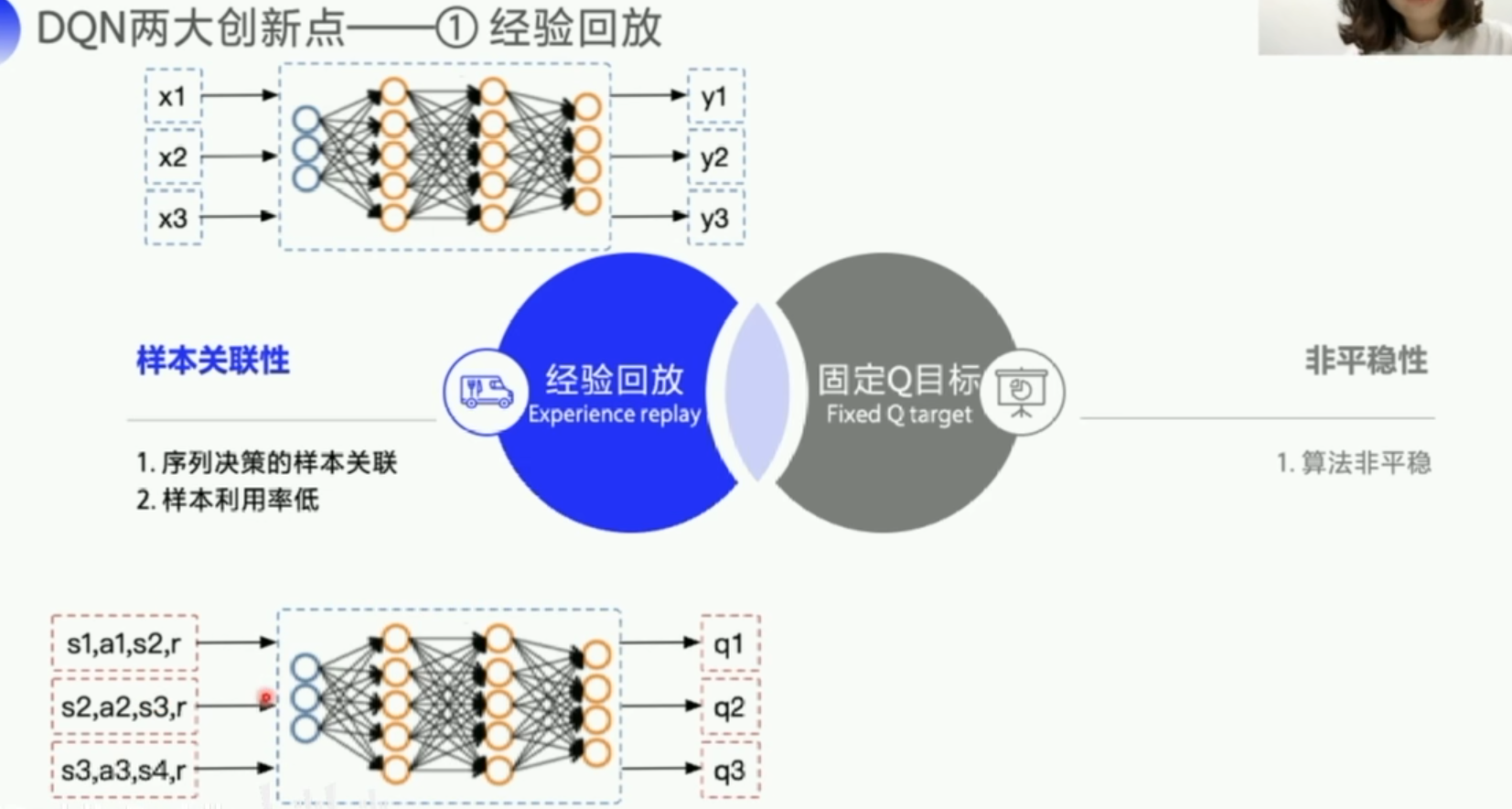
第一个是经验回放。经验回放可以充分利用off-policy的优势,可以利用Behavior Policy探索的数据特征形成一组组数据,并且可以随机打乱,使得神经网络可以重复多次地进行学习。这样可以打乱样本的关联性,而且能提高样本利用率。
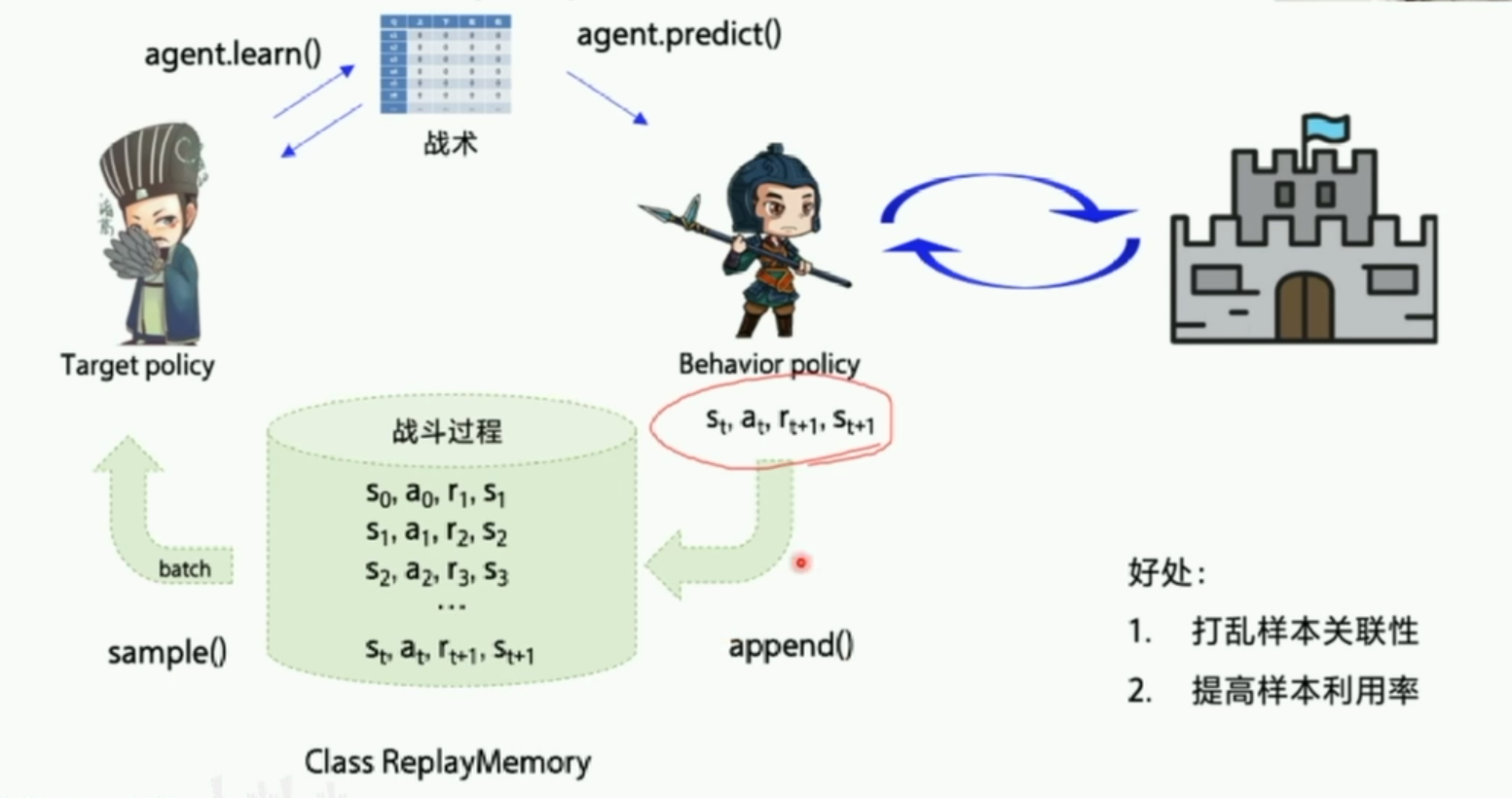
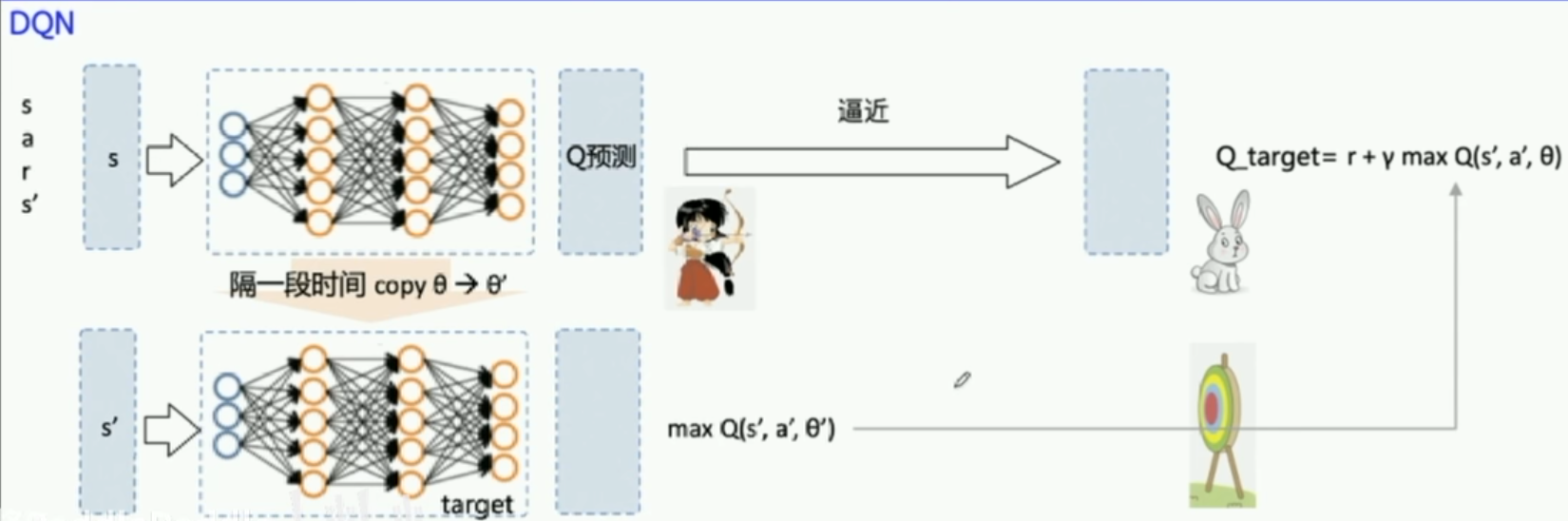
第二个是固定Q目标。增加了算法的平稳性。由于在探索过程中的Q也是时时刻刻都在变化的,因此我们训练的神经网络很难去逼近它的值,因此我们需要把Q值固定一段时间来训练参数,这是Q网络。我们需要另外一个一样的网络(target Q网络),Q网络的作用是产生一个Q预测值,直接用来决策产生action。而target Q是产生一个Q目标值,我们需要训练网络让这两个值越接近越好,这个Loss就是网络需要优化的目标,利用这个Loss我们就可以更新Q网络的参数。刚开始我们的网络的输出是随机的,但是受到reward的影响,各个状态的价值随着更新都会逐渐区分开来。
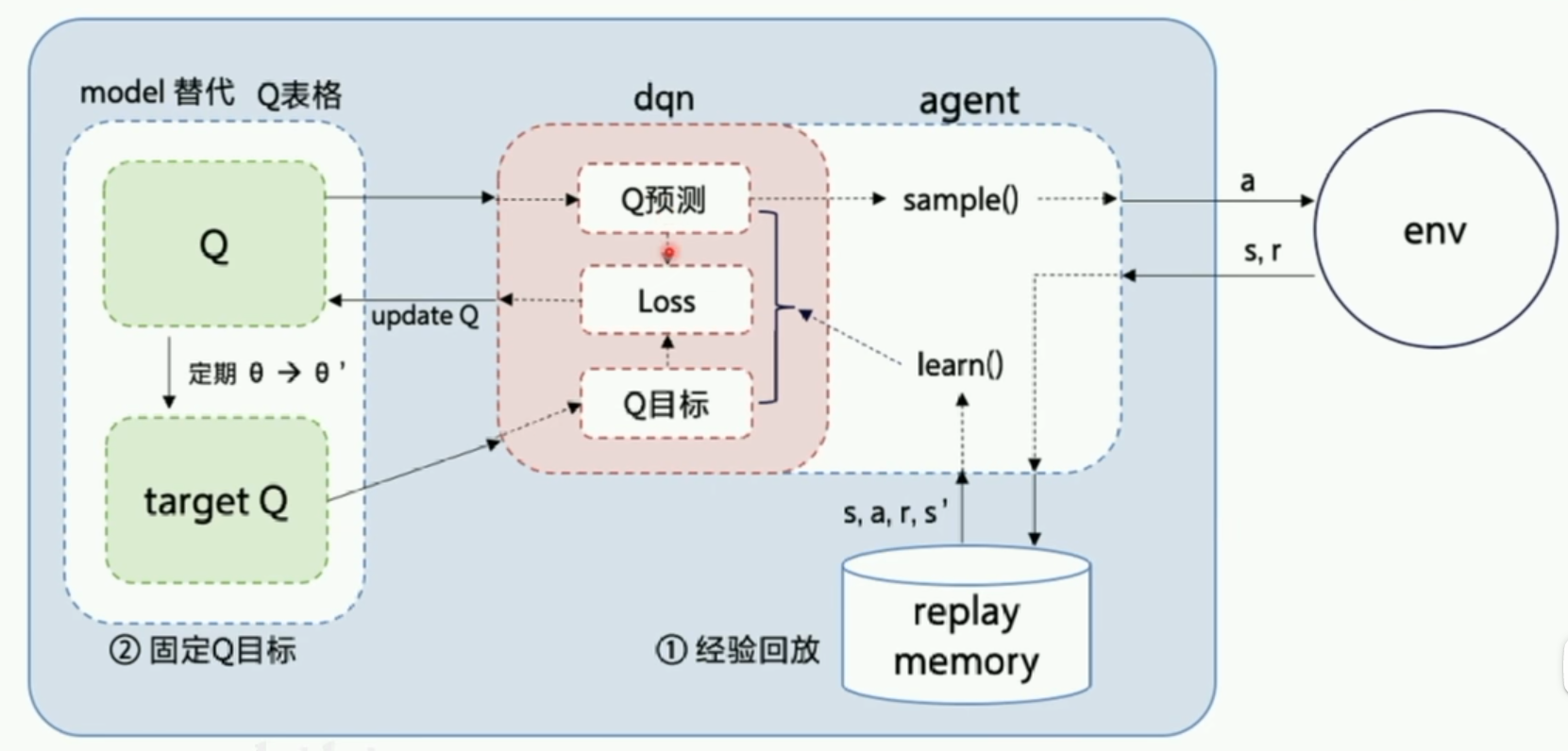
这也是PARL这个框架的特点,它把算法框架拆分为model,algorithm,agent三个部分
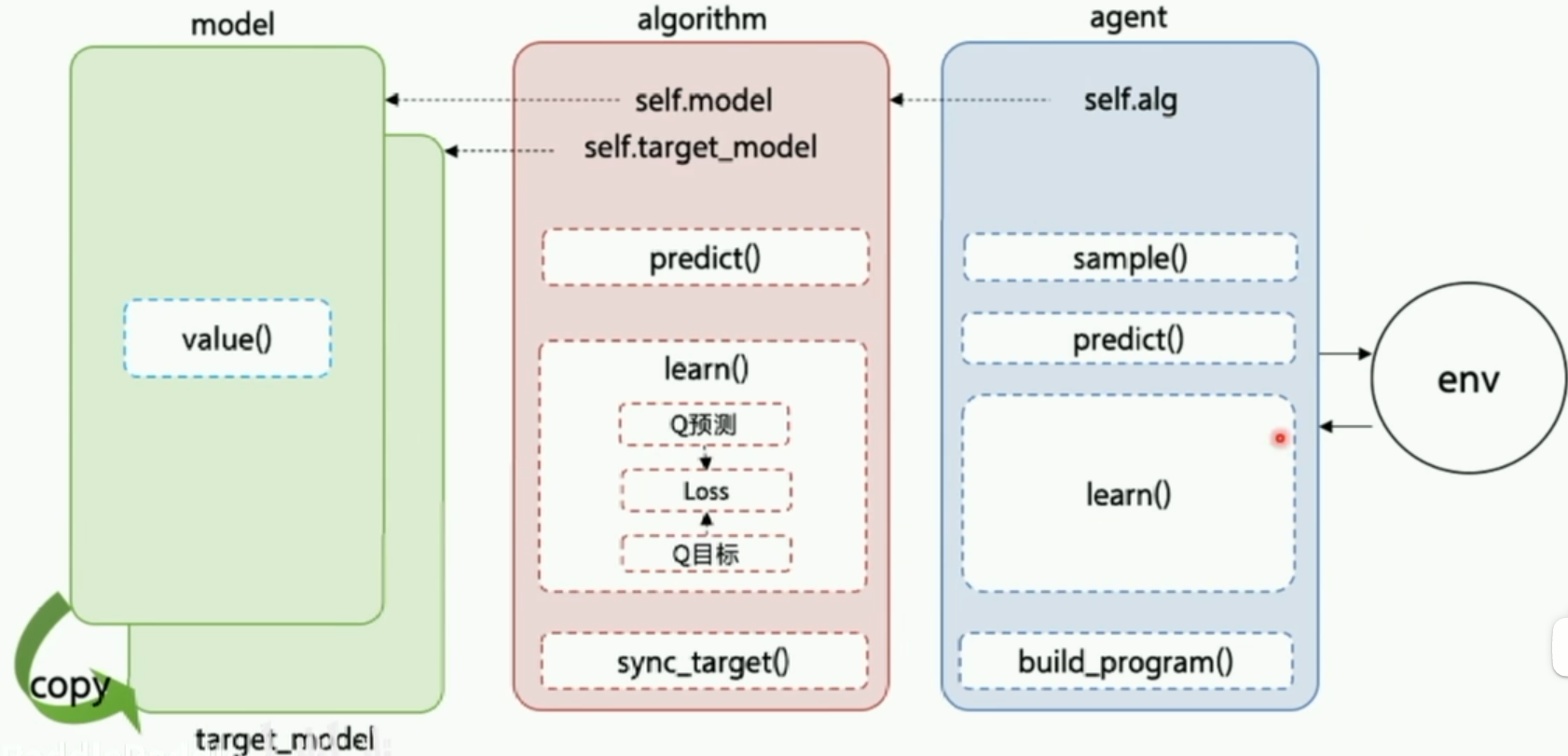
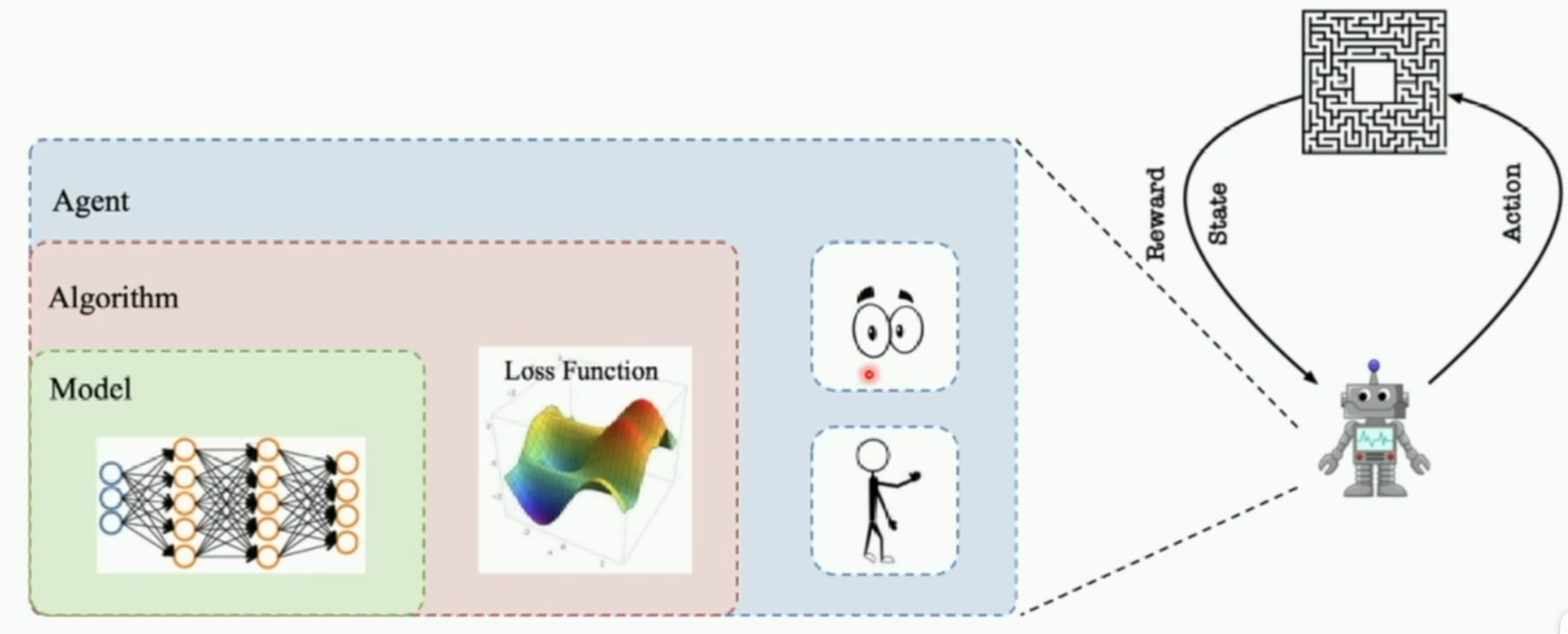
代码实现
reply_memory.py:用来把一个batch的资料分类整理。
class ReplayMemory(object):
def __init__(self, max_size):
# deque是高性能的数据结构之一,是一个队列
self.buffer = collections.deque(maxlen=max_size)
# 往队列中添加一条数据
def append(self, exp):
self.buffer.append(exp)
def sample(self, batch_size):
# 随机取出batch_size条数据
mini_batch = random.sample(self.buffer, batch_size)
obs_batch, action_batch, reward_batch, next_obs_batch, done_batch = [], [], [], [], []
# 数据分类存放到列表中
for experience in mini_batch:
s, a, r, s_p, done = experience
obs_batch.append(s)
action_batch.append(a)
reward_batch.append(r)
next_obs_batch.append(s_p)
done_batch.append(done)
# 返回分类存放一个batch数据的numpy数组
return np.array(obs_batch).astype('float32'), \
np.array(action_batch).astype('float32'), np.array(reward_batch).astype('float32'),\
np.array(next_obs_batch).astype('float32'), np.array(done_batch).astype('float32')
def __len__(self):
return len(self.buffer)
首先是模型model.py:
定义了3层的全连接网络,输入维数为1,输入为act_dim维。中间层分别是128和128个节点的全连接层。
import parl
from parl.core.fluid import layers # 封装了 paddle.fluid.layers 的API
class Model(parl.Model):
# 定义了网络的结构
def __init__(self, act_dim):
hid1_size = 128
hid2_size = 128
# 3层全连接网络
self.fc1 = layers.fc(size=hid1_size, act='relu')
self.fc2 = layers.fc(size=hid2_size, act='relu')
self.fc3 = layers.fc(size=act_dim, act=None)
# 决定了网络的输出
def value(self, obs):
h1 = self.fc1(obs)
h2 = self.fc2(h1)
Q = self.fc3(h2)
return Qalgorithm.py,DQN算法的精髓:
import copy
import paddle.fluid as fluid
import parl
from parl.core.fluid import layers
class DQN(parl.Algorithm):
def __init__(self, model, act_dim=None, gamma=None, lr=None):
""" DQN algorithm
Args:
model (parl.Model): 定义Q函数的前向网络结构
act_dim (int): action空间的维度,即有几个action
gamma (float): reward的衰减因子
lr (float): learning_rate,学习率.
"""
self.model = model
# 复制一个一模一样的网络
self.target_model = copy.deepcopy(model)
# assert插入调试断点到程序,这里用isinstance判断数据类型是否正确,否则抛出异常
assert isinstance(act_dim, int)
assert isinstance(gamma, float)
assert isinstance(lr, float)
self.act_dim = act_dim
self.gamma = gamma
self.lr = lr
# 使用self.model的value网络来获取 [Q(s,a1),Q(s,a2),...]
def predict(self, obs):
return self.model.value(obs)
# 使用DQN算法更新self.model的value网络,传进的参数是一个个数组,是一个batch中的数据,返回Loss
def learn(self, obs, action, reward, next_obs, terminal):
# 从target_model中获取 max Q' 的值,用于计算target_Q
next_pred_value = self.target_model.value(next_obs)
best_v = layers.reduce_max(next_pred_value, dim=1)
best_v.stop_gradient = True # 阻止梯度传递,Target Model不需要训练
terminal = layers.cast(terminal, dtype='float32') # bool变量转换成浮点数
target = reward + (1.0 - terminal) * self.gamma * best_v # 这样就可以把公式统一
pred_value = self.model.value(obs) # 获取Q预测值
# 将action转onehot向量,比如:3 => [0,0,0,1,0]
action_onehot = layers.one_hot(action, self.act_dim)
action_onehot = layers.cast(action_onehot, dtype='float32')
# 下面一行是逐元素相乘,拿到action对应的 Q(s,a)
# 比如:pred_value = [[2.3, 5.7, 1.2, 3.9, 1.4]], action_onehot = [[0,0,0,1,0]]
# ==> pred_action_value = [[3.9]]
pred_action_value = layers.reduce_sum(
layers.elementwise_mul(action_onehot, pred_value), dim=1)
# 计算 Q(s,a) 与 target_Q的均方差,得到loss
cost = layers.square_error_cost(pred_action_value, target)
cost = layers.reduce_mean(cost)
optimizer = fluid.optimizer.Adam(learning_rate=self.lr) # 使用Adam优化器
optimizer.minimize(cost) # 训练
return cost
# 把 self.model 的模型参数值同步到 self.target_model
def sync_target(self):
self.model.sync_weights_to(self.target_model)
我们看看程序是如何更新神经网络的,我们知道神经网络是代替存储Q表格的地方,首先,我们存在两个神经网络,一个输出预测值,一个输出目标值。首先我们需要通过Target Q网络计算输出的目标值,由于网络没有充分训练,这个值是不准确的。然后我们获取了Q网络的预测值,由于它也没有经过充分训练,这个预测值也是不准确的。虽然不准确,但是我们还是需要训练Q网络让预测值靠近依靠Target Q网络计算的目标值。这就是Learn函数做的事情。
agent.py:
import numpy as np
import paddle.fluid as fluid
import parl
from parl.core.fluid import layers
class Agent(parl.Agent):
def __init__(self,algorithm,obs_dim,act_dim,e_greed=0.1,e_greed_decrement=0):
assert isinstance(obs_dim, int)
assert isinstance(act_dim, int)
self.obs_dim = obs_dim
self.act_dim = act_dim
super(Agent, self).__init__(algorithm)
self.global_step = 0
self.update_target_steps = 200 # 每隔200个training steps再把model的参数复制到target_model中
self.e_greed = e_greed # 有一定概率随机选取动作,探索
self.e_greed_decrement = e_greed_decrement # 随着训练逐步收敛,探索的程度慢慢降低
def build_program(self):
self.pred_program = fluid.Program()
self.learn_program = fluid.Program()
with fluid.program_guard(self.pred_program): # 搭建计算图用于 预测动作,定义输入输出变量
obs = layers.data(
name='obs', shape=[self.obs_dim], dtype='float32')
self.value = self.alg.predict(obs)
with fluid.program_guard(self.learn_program): # 搭建计算图用于 更新Q网络,定义输入输出变量
obs = layers.data(
name='obs', shape=[self.obs_dim], dtype='float32')
action = layers.data(name='act', shape=[1], dtype='int32')
reward = layers.data(name='reward', shape=[], dtype='float32')
next_obs = layers.data(
name='next_obs', shape=[self.obs_dim], dtype='float32')
terminal = layers.data(name='terminal', shape=[], dtype='bool')
self.cost = self.alg.learn(obs, action, reward, next_obs, terminal)
def sample(self, obs):
sample = np.random.rand() # 产生0~1之间的小数
if sample < self.e_greed:
act = np.random.randint(self.act_dim) # 探索:每个动作都有概率被选择
else:
act = self.predict(obs) # 选择最优动作
self.e_greed = max(
0.01, self.e_greed - self.e_greed_decrement) # 随着训练逐步收敛,探索的程度慢慢降低
return act
def predict(self, obs): # 选择最优动作
obs = np.expand_dims(obs, axis=0)
pred_Q = self.fluid_executor.run(
self.pred_program,
feed={'obs': obs.astype('float32')},
fetch_list=[self.value])[0]
pred_Q = np.squeeze(pred_Q, axis=0)
act = np.argmax(pred_Q) # 选择Q最大的下标,即对应的动作
return act
def learn(self, obs, act, reward, next_obs, terminal):
# 每隔200个training steps同步一次model和target_model的参数
if self.global_step % self.update_target_steps == 0:
self.alg.sync_target()
self.global_step += 1
act = np.expand_dims(act, -1)
feed = {
'obs': obs.astype('float32'),
'act': act.astype('int32'),
'reward': reward,
'next_obs': next_obs.astype('float32'),
'terminal': terminal
}
cost = self.fluid_executor.run(
self.learn_program, feed=feed, fetch_list=[self.cost])[0] # 训练一次网络
return costtrain.py:执行代码所在
import os
import gym
import numpy as np
import parl
from parl.utils import logger # 日志打印工具
from model import Model
from algorithm import DQN
#from parl.algorithms import DQN
from agent import Agent
from replay_memory import ReplayMemory
LEARN_FREQ = 5 # 训练频率,不需要每一个step都learn,攒一些新增经验后再learn,提高效率
MEMORY_SIZE = 20000 # replay memory的大小,越大越占用内存
MEMORY_WARMUP_SIZE = 200 # replay_memory 里需要预存一些经验数据,再从里面sample一个batch的经验让agent去learn
BATCH_SIZE = 32 # 每次给agent learn的数据数量,从replay memory随机里sample一批数据出来
LEARNING_RATE = 0.001 # 学习率
GAMMA = 0.99 # reward 的衰减因子,一般取 0.9 到 0.999 不等
# 训练一个episode
def run_episode(env, agent, rpm):
total_reward = 0
obs = env.reset()
step = 0
while True:
step += 1
action = agent.sample(obs) # 采样动作,所有动作都有概率被尝试到
next_obs, reward, done, _ = env.step(action)
rpm.append((obs, action, reward, next_obs, done))
# train model
if (len(rpm) > MEMORY_WARMUP_SIZE) and (step % LEARN_FREQ == 0):
(batch_obs, batch_action, batch_reward, batch_next_obs,
batch_done) = rpm.sample(BATCH_SIZE)
train_loss = agent.learn(batch_obs, batch_action, batch_reward,
batch_next_obs,
batch_done) # s,a,r,s',done
total_reward += reward
obs = next_obs
if done:
break
return total_reward
# 评估 agent, 跑 5 个episode,总reward求平均
def evaluate(env, agent, render=False):
eval_reward = []
for i in range(5):
obs = env.reset()
episode_reward = 0
while True:
action = agent.predict(obs) # 预测动作,只选最优动作
obs, reward, done, _ = env.step(action)
episode_reward += reward
if render:
env.render()
if done:
break
eval_reward.append(episode_reward)
return np.mean(eval_reward)
def main():
env = gym.make(
'CartPole-v0'
) # CartPole-v0: expected reward > 180 MountainCar-v0 : expected reward > -120
action_dim = env.action_space.n # CartPole-v0: 2
obs_shape = env.observation_space.shape # CartPole-v0: (4,)
rpm = ReplayMemory(MEMORY_SIZE) # DQN的经验回放池
# 根据parl框架构建agent
model = Model(act_dim=action_dim)
algorithm = DQN(model, act_dim=action_dim, gamma=GAMMA, lr=LEARNING_RATE)
agent = Agent(
algorithm,
obs_dim=obs_shape[0],
act_dim=action_dim,
e_greed=0.1, # 有一定概率随机选取动作,探索
e_greed_decrement=1e-6) # 随着训练逐步收敛,探索的程度慢慢降低
# 加载模型
# save_path = './dqn_model.ckpt'
# agent.restore(save_path)
# 先往经验池里存一些数据,避免最开始训练的时候样本丰富度不够
while len(rpm) < MEMORY_WARMUP_SIZE:
run_episode(env, agent, rpm)
max_episode = 2000
# start train
episode = 0
while episode < max_episode: # 训练max_episode个回合,test部分不计算入episode数量
# train part
for i in range(0, 50):
total_reward = run_episode(env, agent, rpm)
episode += 1
# test part
eval_reward = evaluate(env, agent, render=True) # render=True 查看显示效果
logger.info('episode:{} e_greed:{} Test reward:{}'.format(
episode, agent.e_greed, eval_reward))
# 训练结束,保存模型
save_path = './dqn_model.ckpt'
agent.save(save_path)
if __name__ == '__main__':
main()
由于库的版本问题,我这里是运行失败的,原因是parl没有layers这个类。。。所以这里我只知道一些实现思路,如果知道新版的代码写法,可以联系我。
CartPole
CartPole的环境相当于强化学习中的“Hello World”,是最基础的环境,任何强化学习算法都可以在上面运行并测试是否收敛。

PARL常用API

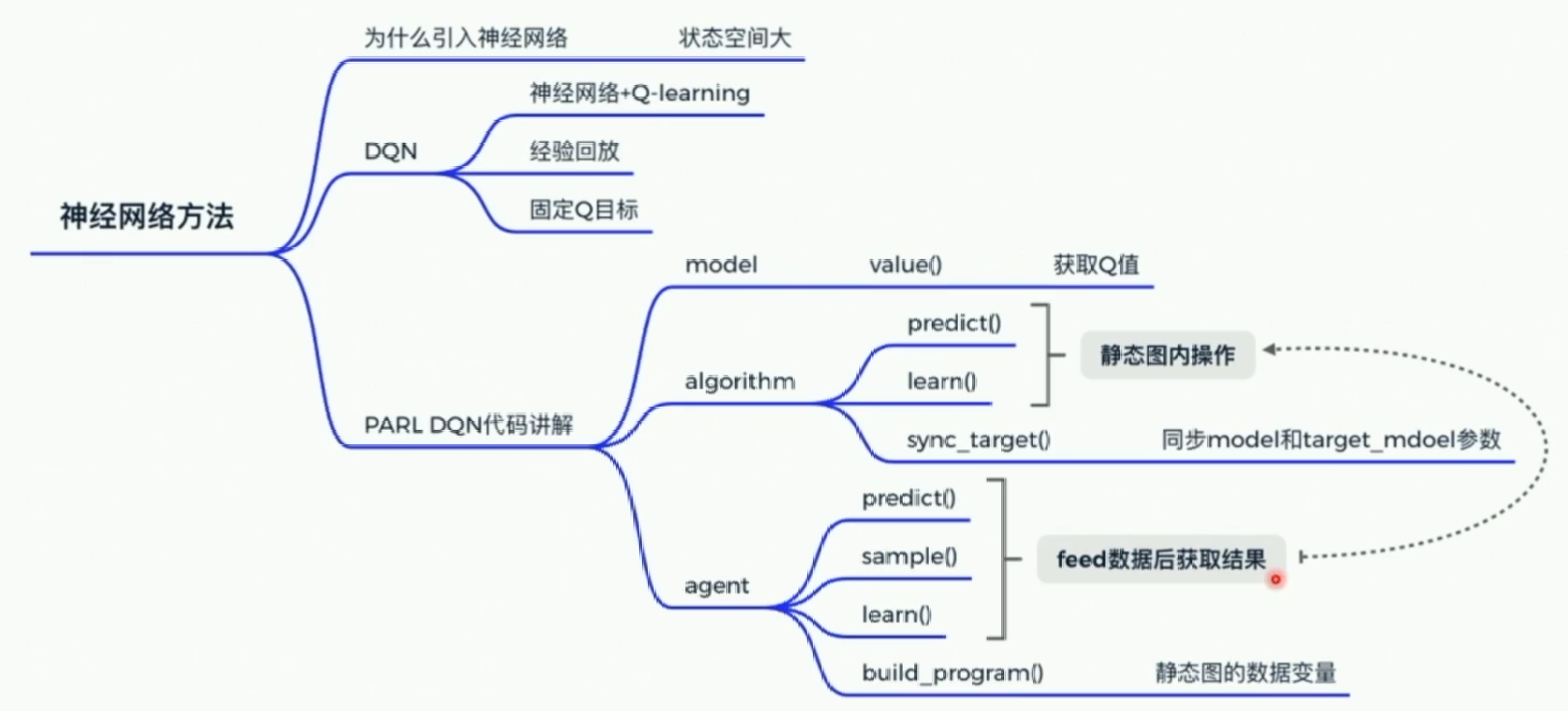
基于策略梯度求解RL
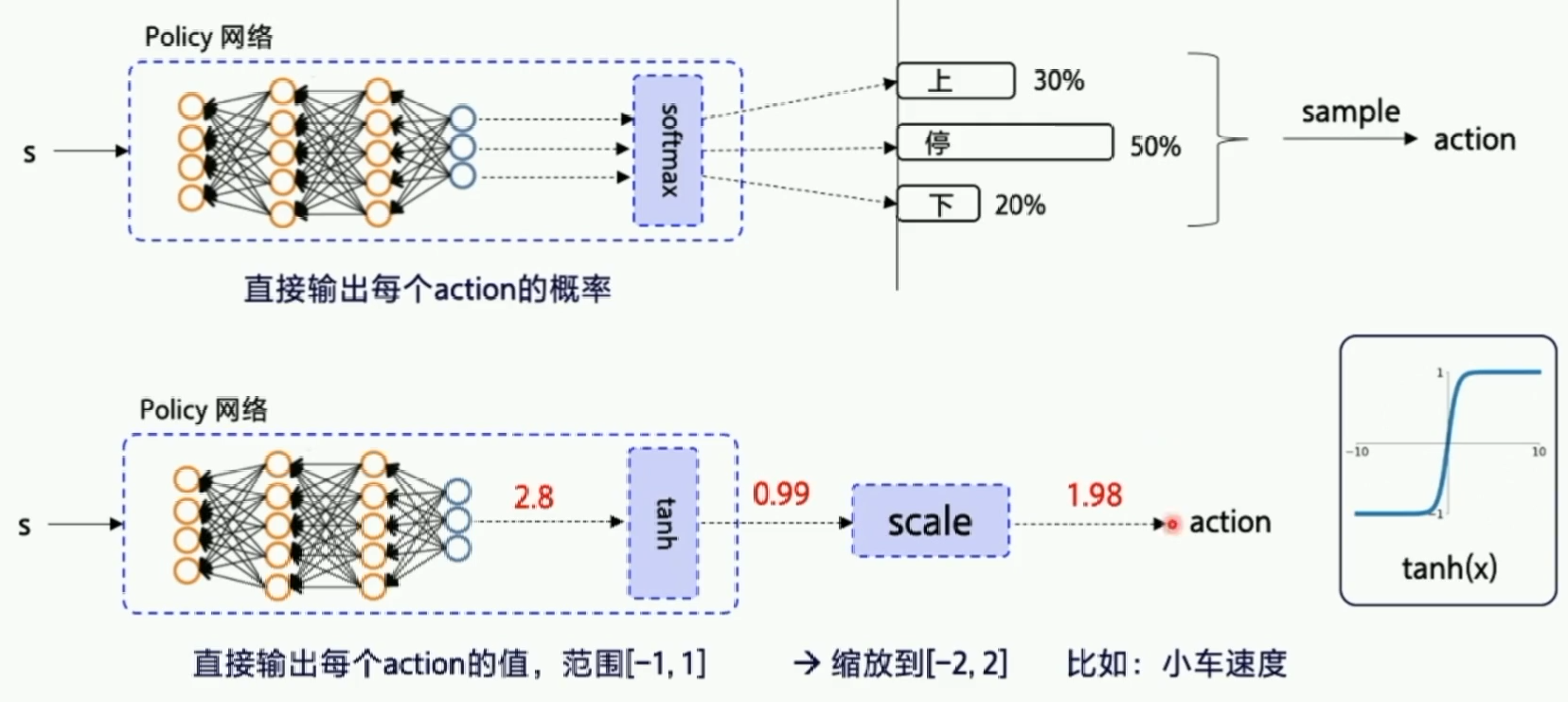
上面我们所学的是value-based,通过探索将Q价值更新到最优,然后根据Q价值来选择最优的动作。下面我们讲policy-based,动作选择不再依赖价值函数,而是根据一个策略走到底,看最后的总收益决定算法好坏,好Action将在以后有更大的概率被随机到。
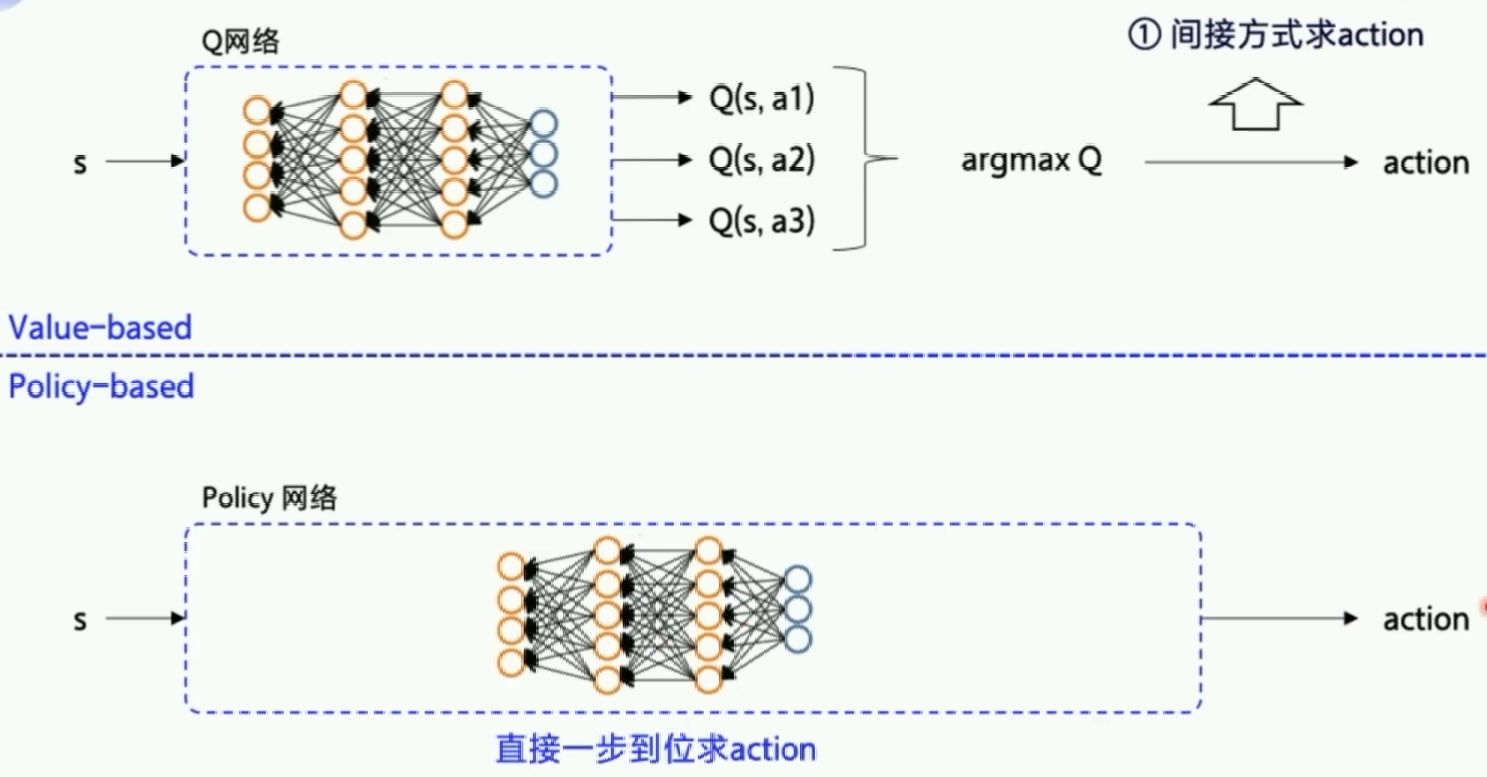
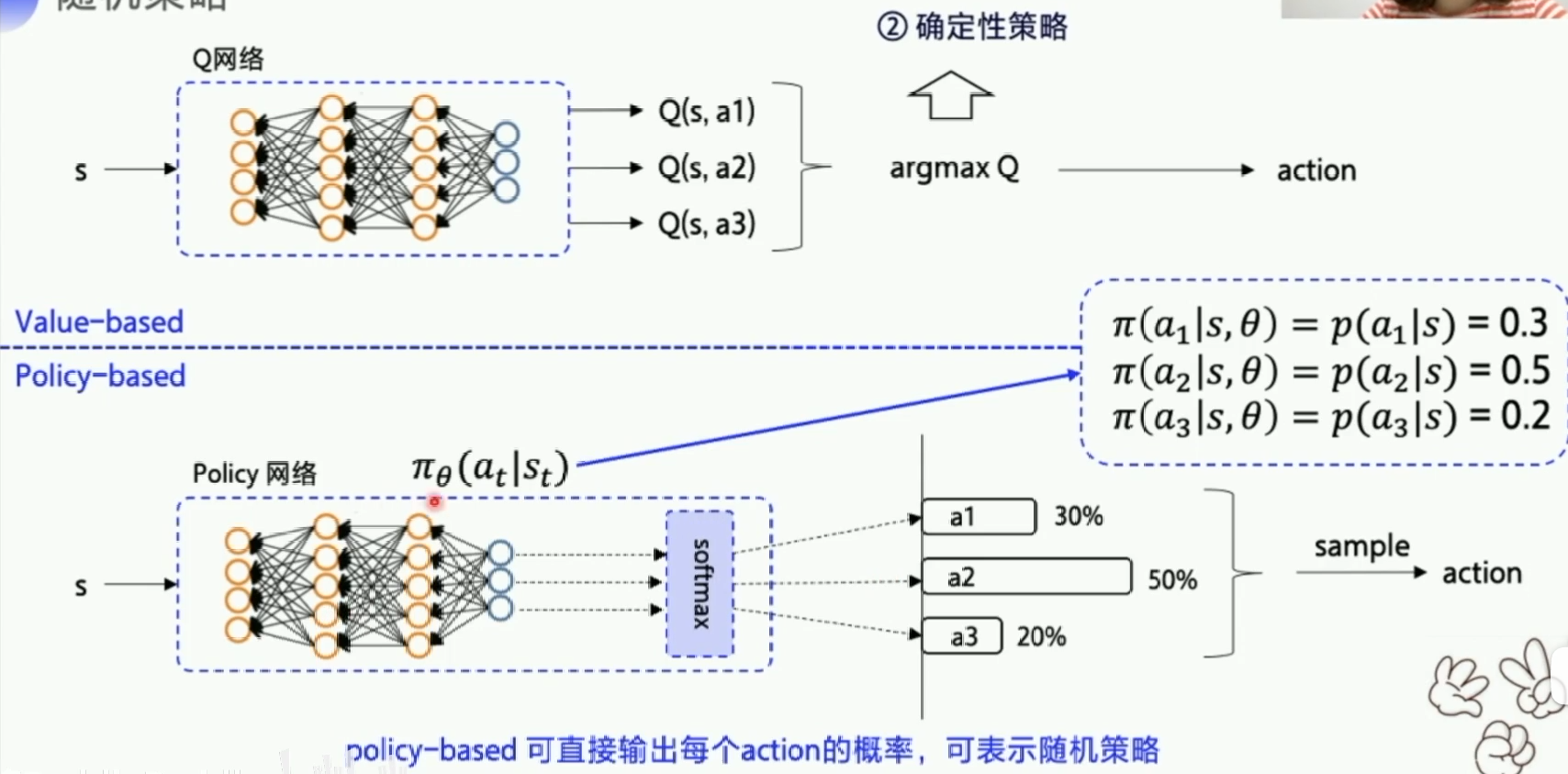
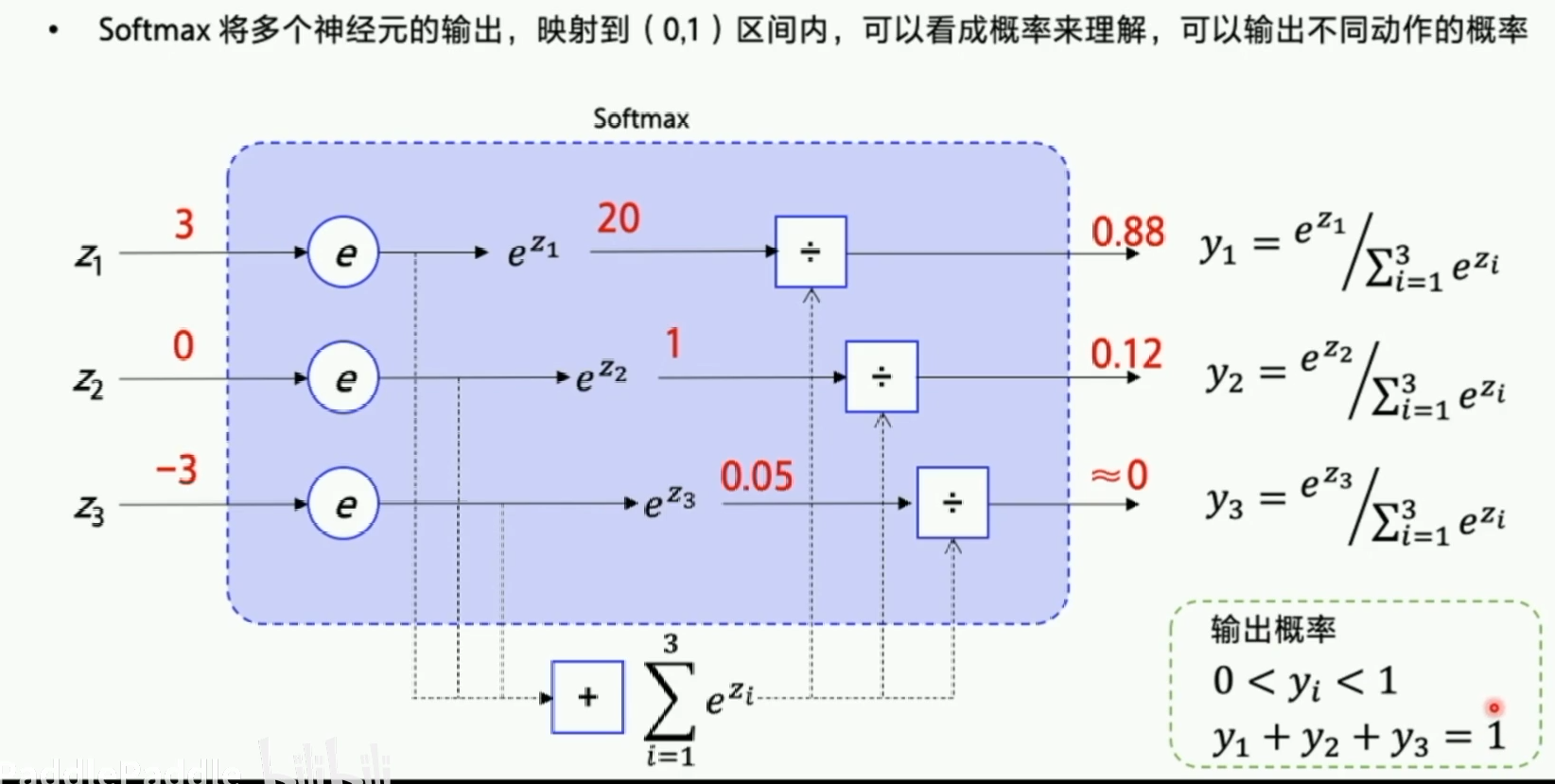
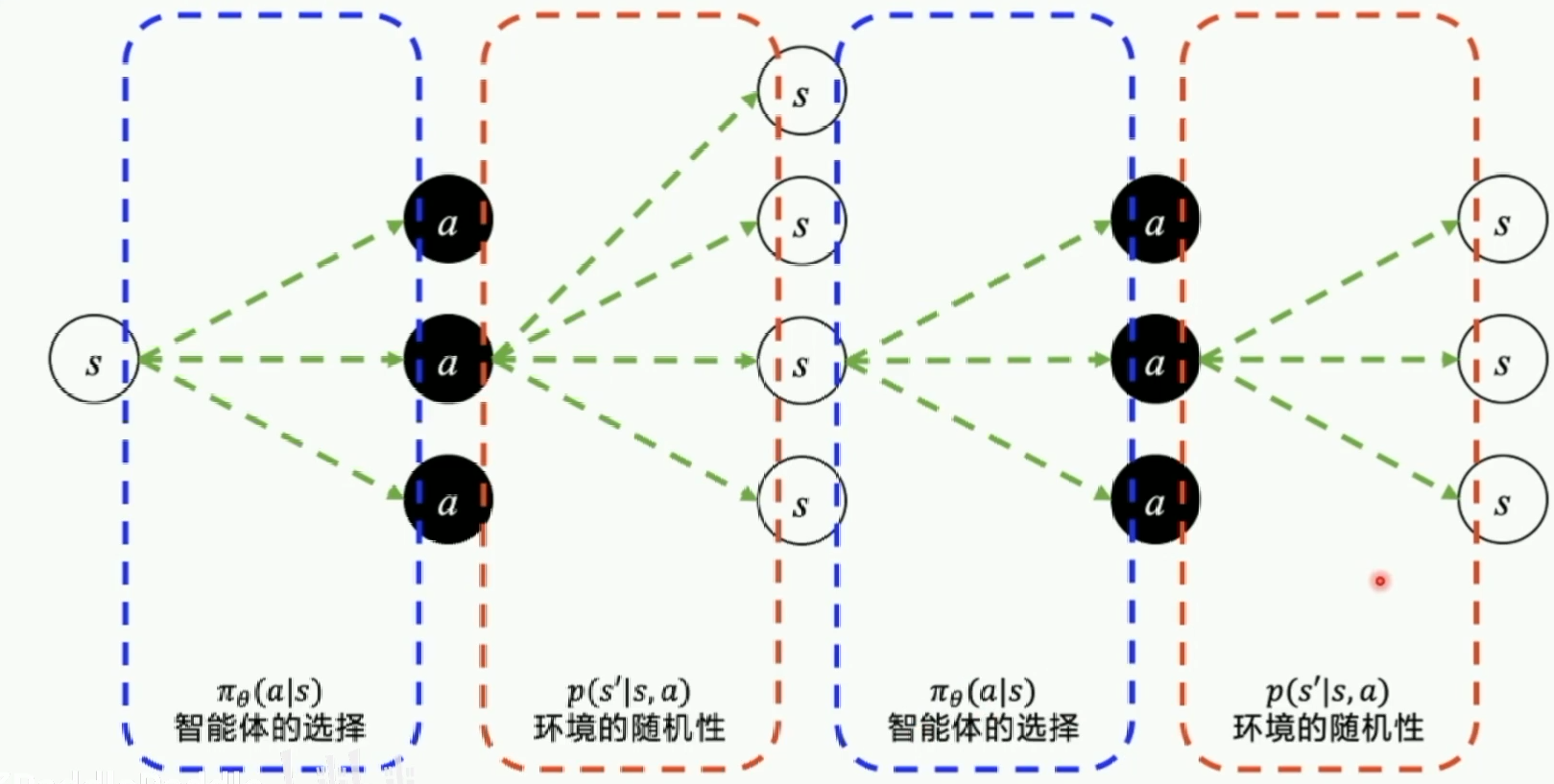
可以看到,智能体通过直接输出一个动作选择的概率来选择下一步的action,这个策略是可以优化的,但是执行一个action之后有多种状态的可能性,这也就是环境的随机性。不断输出动作到新的状态到游戏结束称为完成一个episode,这一串的交互称为一个episode的轨迹(Trajectory)。
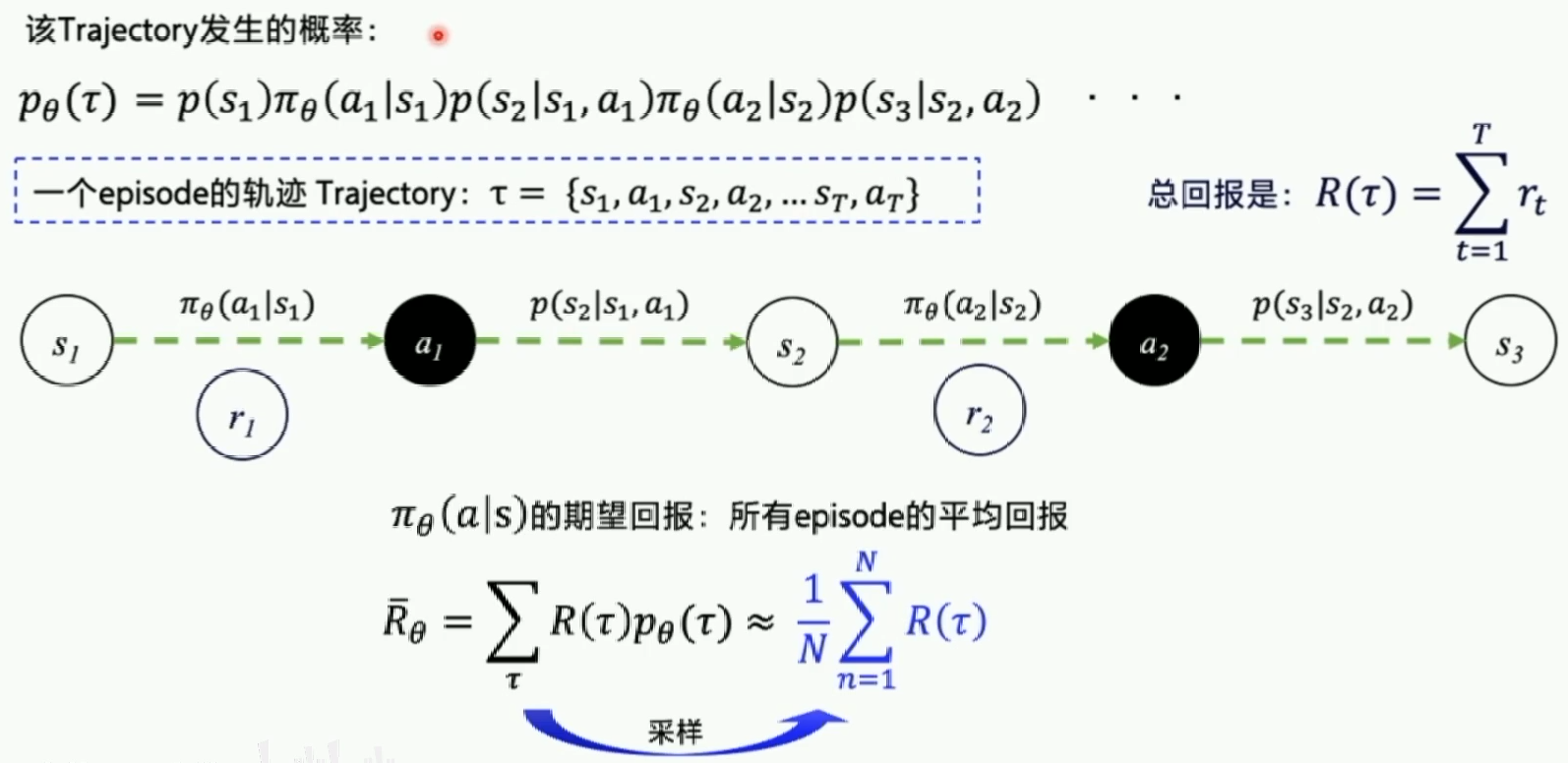
期望回报是穷举所有在该策略下的轨迹能拿到的回报(Reward)的平均值,在实际运用中我们无法穷举,也不能得出状态转移概率,但是我们可以通过运行多个episode然后将得到的reward取平均近似认为是期望回报。
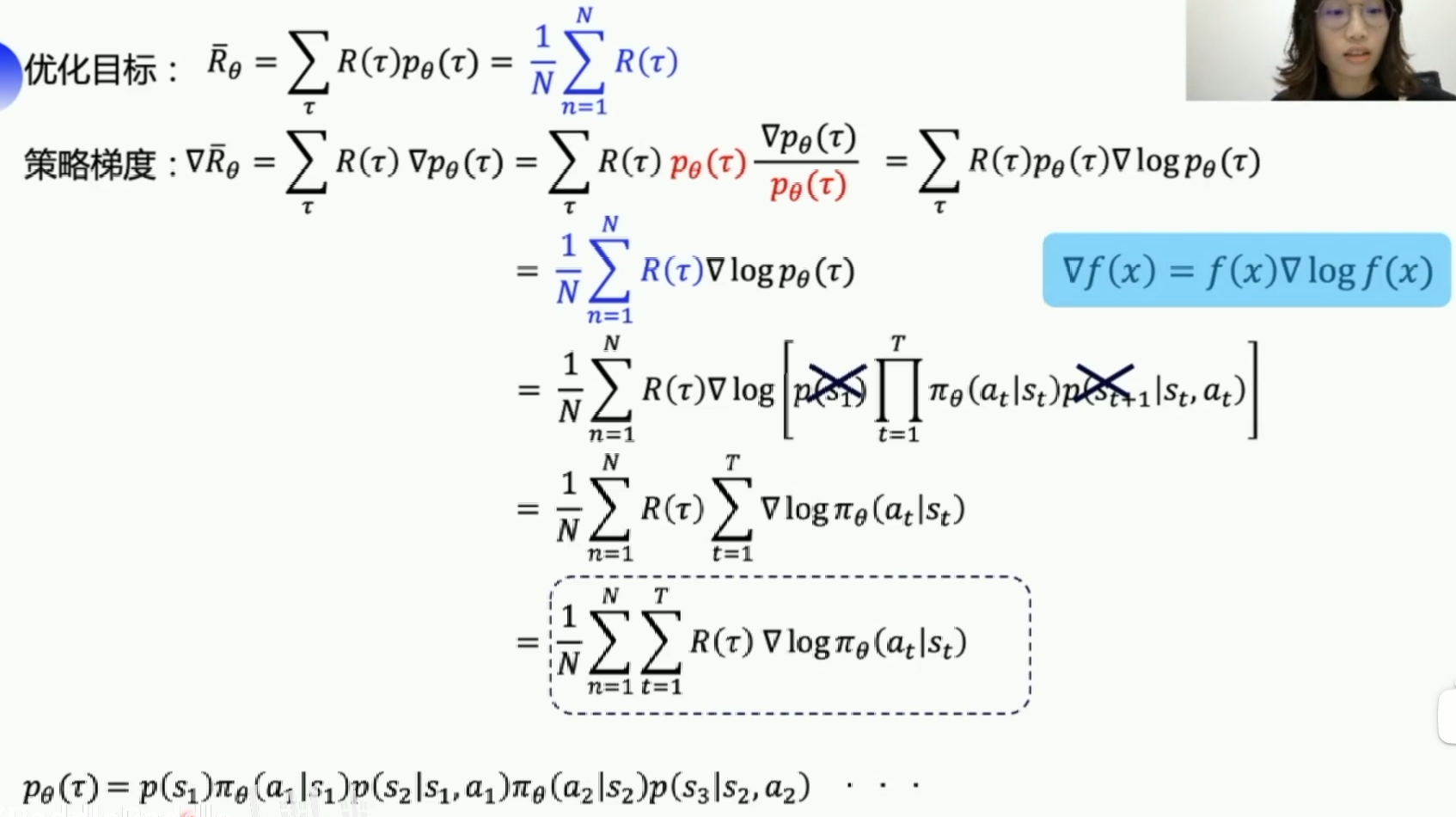
由于我们没有label对我们的网络进行更新,这时候就需要利用我们的期望回报了,我们通过梯度上升法使得我们的reward变大,那么就能使得策略变好,经过推导可以得出我们更新的梯度公式如下:
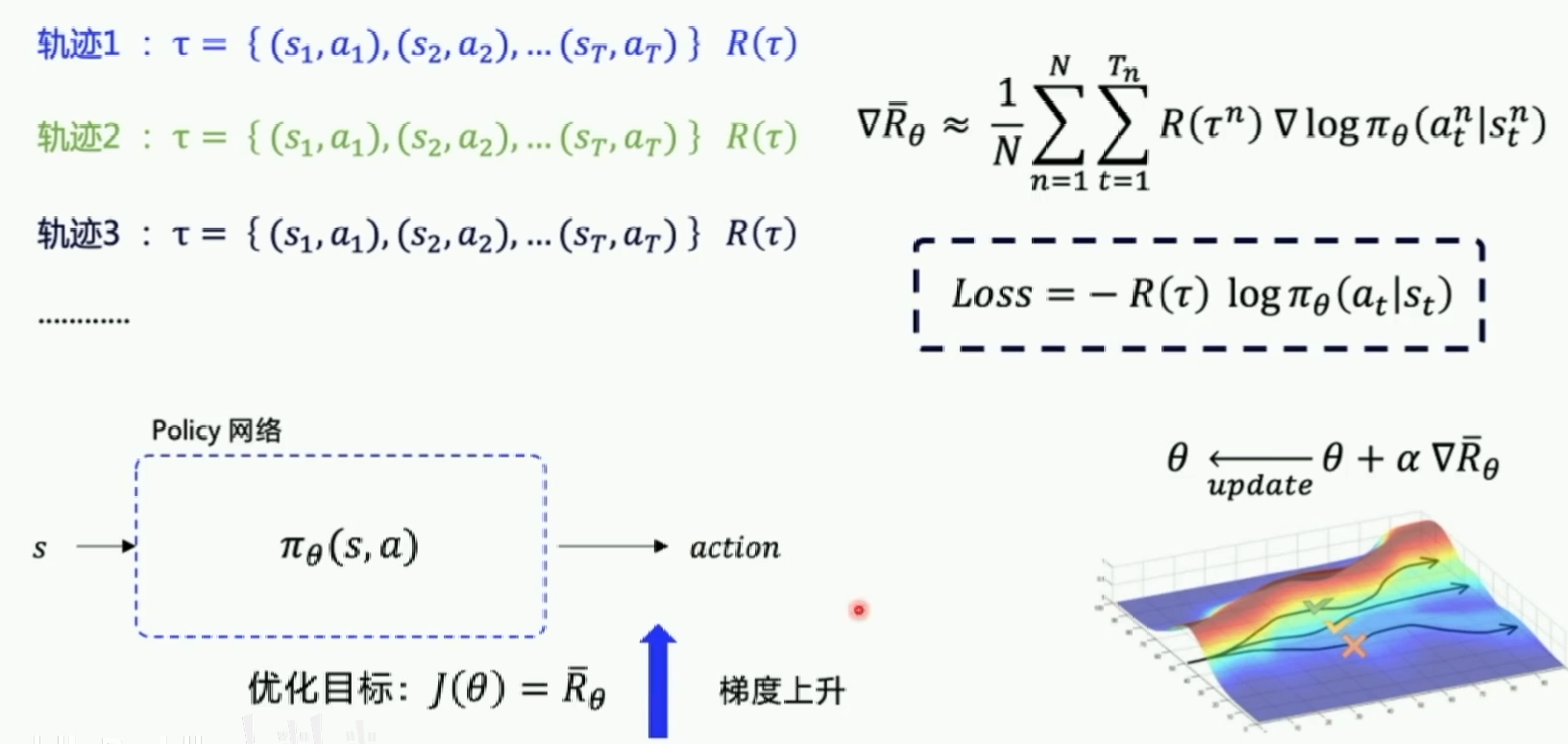
蒙特卡洛(MC)和时序差分(TD)

蒙特卡洛是完成一个episode之后,再做一次更新,其中$G_t$指的是在一个step之后能拿到的总收益之和。而时序差分指的是每一个step都更新数据。用的是Q function来近似表示总收益。

Policy Gradient
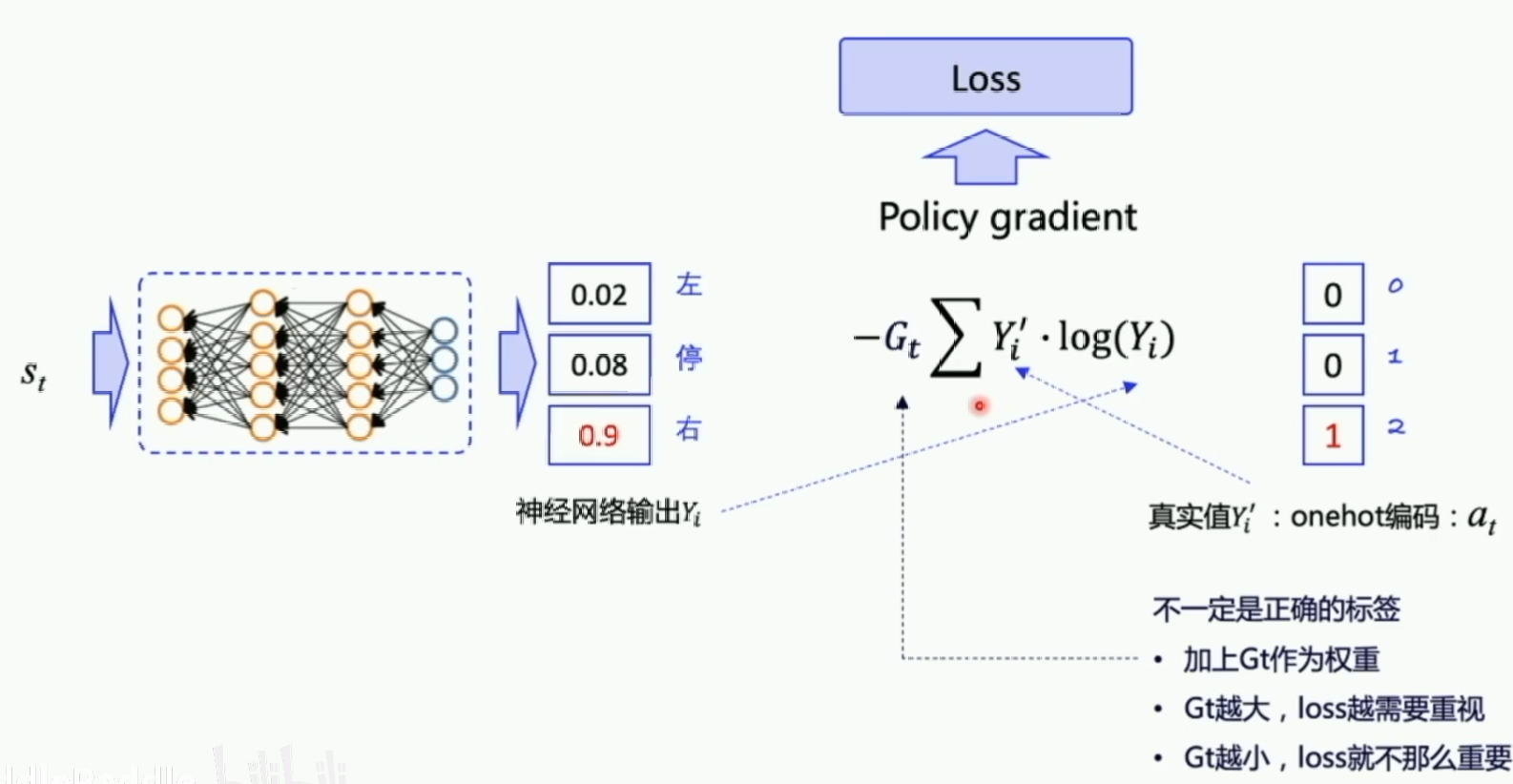
重点来了!!!我们使用的更新方式是Policy Gradient,也就是策略梯度,我们的loss依旧通过交叉熵方式获得,但还需要乘以一个$G_t$作为权重,也就是我们计算出来的总收益!总收益越高的说明我们的决策越好,$G_t$越大,我网络会用较大的梯度来进行更新,反之$G_t$较小则用小梯度更新。这样进行多次更新之后,我们网络算出来的决策就会越来越趋近于好的决策。
对于离散的动作,我们直接采用价值计算的原始公式,然后用梯度上升法即可,具体操作可以用蒙泰卡罗采样的方法代替:

对于连续动作(对于离散动作同样适用),例如代码中的例子:

总结:

其中对于每个动作价值Q的计算都是在完成一个episode之后,利用带折扣的Reward从后往前进行计算的。还有一种就是利用神经网络来近似价值函数的方法,称为Actor-Critic。
对应代码:
def learn(self, obs, action, reward):
""" 用policy gradient 算法更新policy model
"""
act_prob = self.model(obs) # 获取输出动作概率
# log_prob = layers.cross_entropy(act_prob, action) # 交叉熵
log_prob = layers.reduce_sum(
-1.0 * layers.log(act_prob) * layers.one_hot(
action, act_prob.shape[1]),
dim=1)
cost = log_prob * reward
cost = layers.reduce_mean(cost)
optimizer = fluid.optimizer.Adam(self.lr)
optimizer.minimize(cost)
return cost
流程及代码:
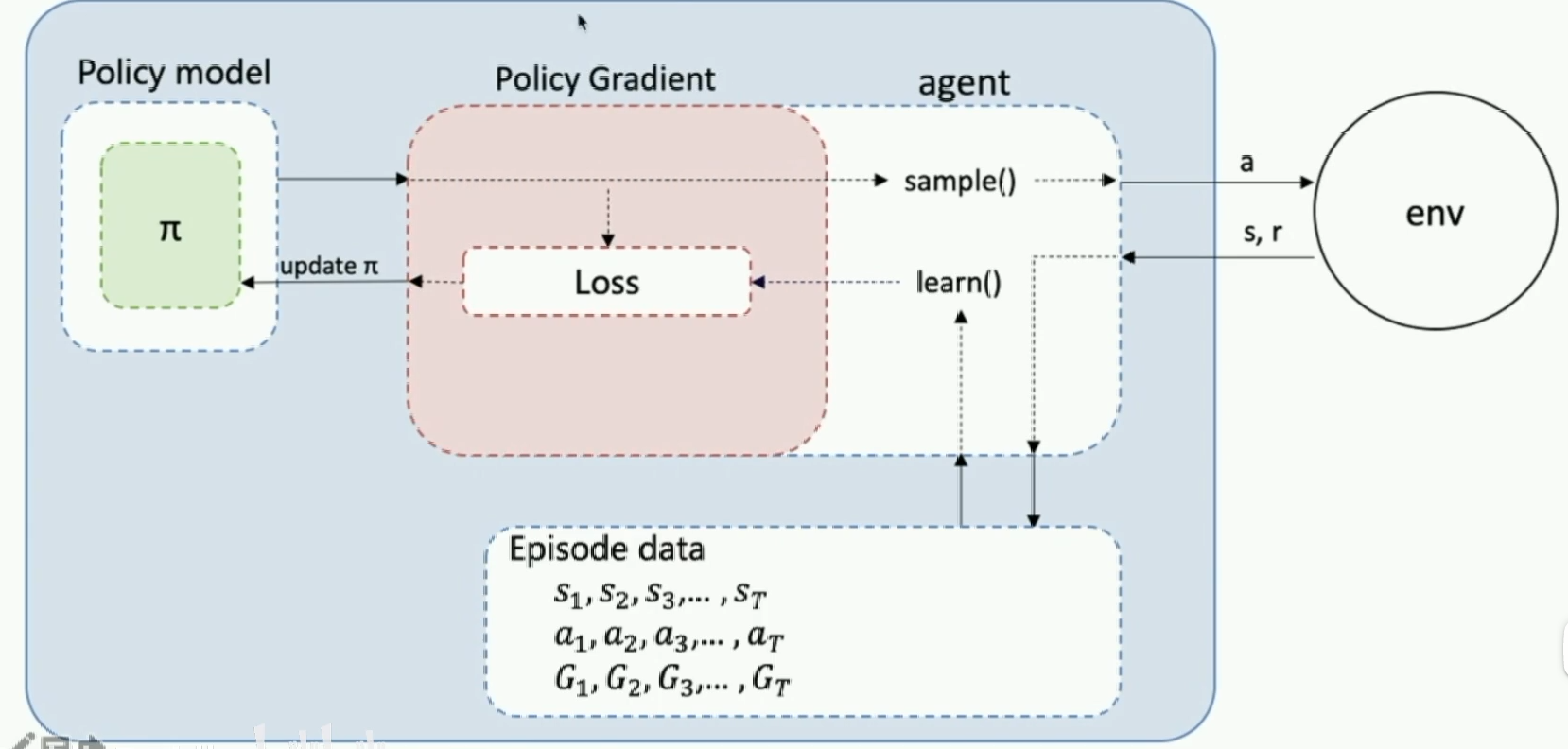
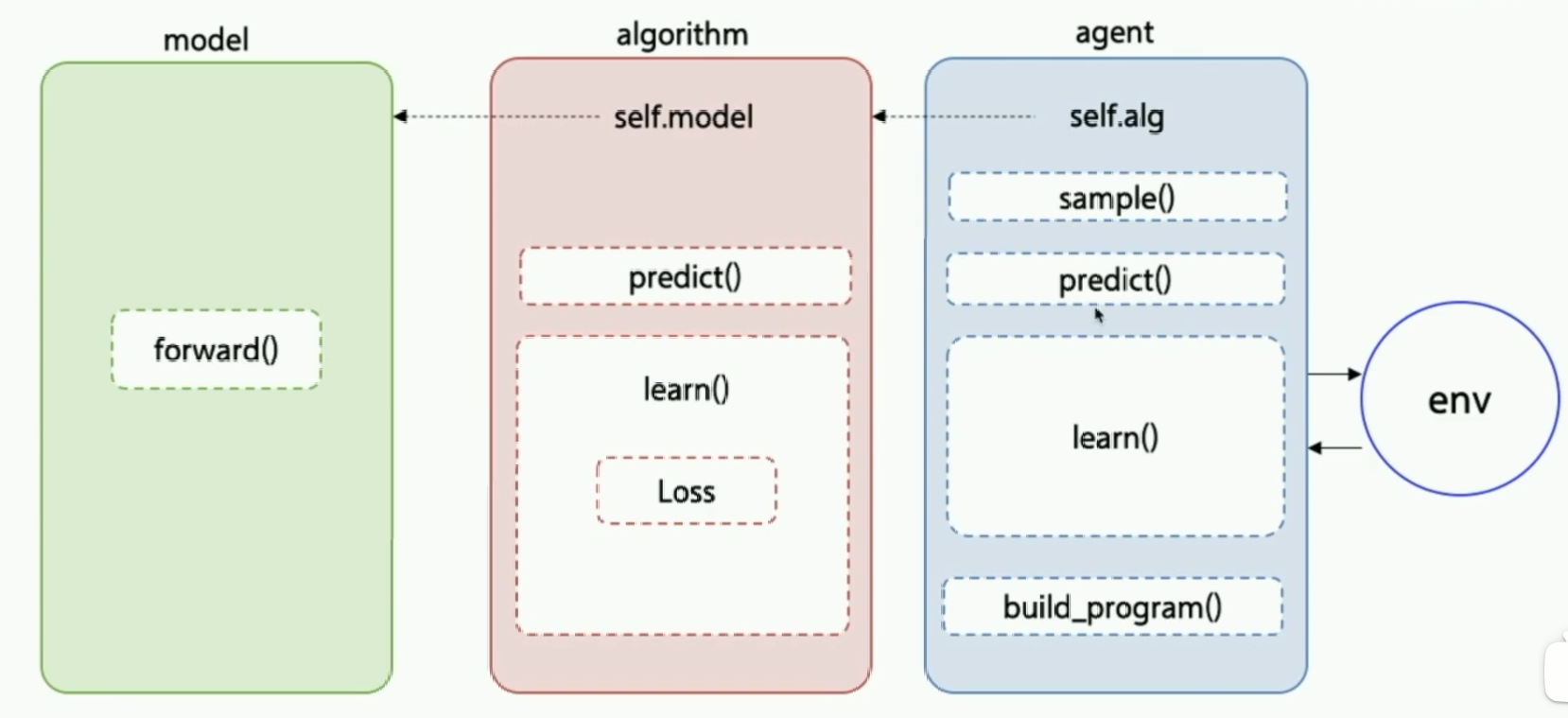
model.py:
import parl
from parl import layers
class Model(parl.Model):
def __init__(self, act_dim):
act_dim = act_dim
hid1_size = act_dim * 10
self.fc1 = layers.fc(size=hid1_size, act='tanh')
self.fc2 = layers.fc(size=act_dim, act='softmax')
def forward(self, obs): # 可直接用 model = Model(5); model(obs)调用
out = self.fc1(obs)
out = self.fc2(out)
return out
algorithm.py:
import paddle.fluid as fluid
import parl
from parl import layers
class PolicyGradient(parl.Algorithm):
def __init__(self, model, lr=None):
self.model = model
assert isinstance(lr, float)
self.lr = lr
def predict(self, obs):
""" 使用policy model预测输出的动作概率
"""
return self.model(obs)
def learn(self, obs, action, reward):
""" 用policy gradient 算法更新policy model
"""
act_prob = self.model(obs) # 获取输出动作概率
# log_prob = layers.cross_entropy(act_prob, action) # 交叉熵
log_prob = layers.reduce_sum(
-1.0 * layers.log(act_prob) * layers.one_hot(
action, act_prob.shape[1]),
dim=1)
cost = log_prob * reward
cost = layers.reduce_mean(cost)
optimizer = fluid.optimizer.Adam(self.lr)
optimizer.minimize(cost)
return cost
agent.py:
import numpy as np
import paddle.fluid as fluid
import parl
from parl import layers
class Agent(parl.Agent):
def __init__(self, algorithm, obs_dim, act_dim):
self.obs_dim = obs_dim
self.act_dim = act_dim
super(Agent, self).__init__(algorithm)
def build_program(self):
self.pred_program = fluid.Program()
self.learn_program = fluid.Program()
with fluid.program_guard(self.pred_program): # 搭建计算图用于 预测动作,定义输入输出变量
obs = layers.data(
name='obs', shape=[self.obs_dim], dtype='float32')
self.act_prob = self.alg.predict(obs)
with fluid.program_guard(
self.learn_program): # 搭建计算图用于 更新policy网络,定义输入输出变量
obs = layers.data(
name='obs', shape=[self.obs_dim], dtype='float32')
act = layers.data(name='act', shape=[1], dtype='int64')
reward = layers.data(name='reward', shape=[], dtype='float32')
self.cost = self.alg.learn(obs, act, reward)
def sample(self, obs):
obs = np.expand_dims(obs, axis=0) # 增加一维维度
act_prob = self.fluid_executor.run(
self.pred_program,
feed={'obs': obs.astype('float32')},
fetch_list=[self.act_prob])[0]
act_prob = np.squeeze(act_prob, axis=0) # 减少一维维度
act = np.random.choice(range(self.act_dim), p=act_prob) # 根据动作概率选取动作
return act
def predict(self, obs):
obs = np.expand_dims(obs, axis=0)
act_prob = self.fluid_executor.run(
self.pred_program,
feed={'obs': obs.astype('float32')},
fetch_list=[self.act_prob])[0]
act_prob = np.squeeze(act_prob, axis=0)
act = np.argmax(act_prob) # 根据动作概率选择概率最高的动作
return act
def learn(self, obs, act, reward):
act = np.expand_dims(act, axis=-1)
feed = {
'obs': obs.astype('float32'),
'act': act.astype('int64'),
'reward': reward.astype('float32')
}
cost = self.fluid_executor.run(
self.learn_program, feed=feed, fetch_list=[self.cost])[0]
return cost
train.py:
import gym
import numpy as np
import parl
from agent import Agent
from model import Model
from algorithm import PolicyGradient # from parl.algorithms import PolicyGradient
from parl.utils import logger
LEARNING_RATE = 1e-3
# 训练一个episode
def run_episode(env, agent):
obs_list, action_list, reward_list = [], [], []
obs = env.reset()
while True:
obs_list.append(obs)
action = agent.sample(obs)
action_list.append(action)
obs, reward, done, info = env.step(action)
reward_list.append(reward)
if done:
break
return obs_list, action_list, reward_list
# 评估 agent, 跑 5 个episode,总reward求平均
def evaluate(env, agent, render=False):
eval_reward = []
for i in range(5):
obs = env.reset()
episode_reward = 0
while True:
action = agent.predict(obs)
obs, reward, isOver, _ = env.step(action)
episode_reward += reward
if render:
env.render()
if isOver:
break
eval_reward.append(episode_reward)
return np.mean(eval_reward)
def calc_reward_to_go(reward_list, gamma=1.0):
for i in range(len(reward_list) - 2, -1, -1):
# G_i = r_i + γ·G_i+1
reward_list[i] += gamma * reward_list[i + 1] # Gt
return np.array(reward_list)
def main():
env = gym.make('CartPole-v0')
# env = env.unwrapped # Cancel the minimum score limit
obs_dim = env.observation_space.shape[0]
act_dim = env.action_space.n
logger.info('obs_dim {}, act_dim {}'.format(obs_dim, act_dim))
# 根据parl框架构建agent
model = Model(act_dim=act_dim)
alg = PolicyGradient(model, lr=LEARNING_RATE)
agent = Agent(alg, obs_dim=obs_dim, act_dim=act_dim)
# 加载模型
# if os.path.exists('./model.ckpt'):
# agent.restore('./model.ckpt')
# run_episode(env, agent, train_or_test='test', render=True)
# exit()
for i in range(1000):
obs_list, action_list, reward_list = run_episode(env, agent)
if i % 10 == 0:
logger.info("Episode {}, Reward Sum {}.".format(
i, sum(reward_list)))
batch_obs = np.array(obs_list)
batch_action = np.array(action_list)
batch_reward = calc_reward_to_go(reward_list)
agent.learn(batch_obs, batch_action, batch_reward)
if (i + 1) % 100 == 0:
total_reward = evaluate(env, agent, render=True)
logger.info('Test reward: {}'.format(total_reward))
# save the parameters to ./model.ckpt
agent.save('./model.ckpt')
if __name__ == '__main__':
main()
由于库的版本问题,这里依旧没有运行成功。
连续动作空间上求解RL
离散动作和连续动作
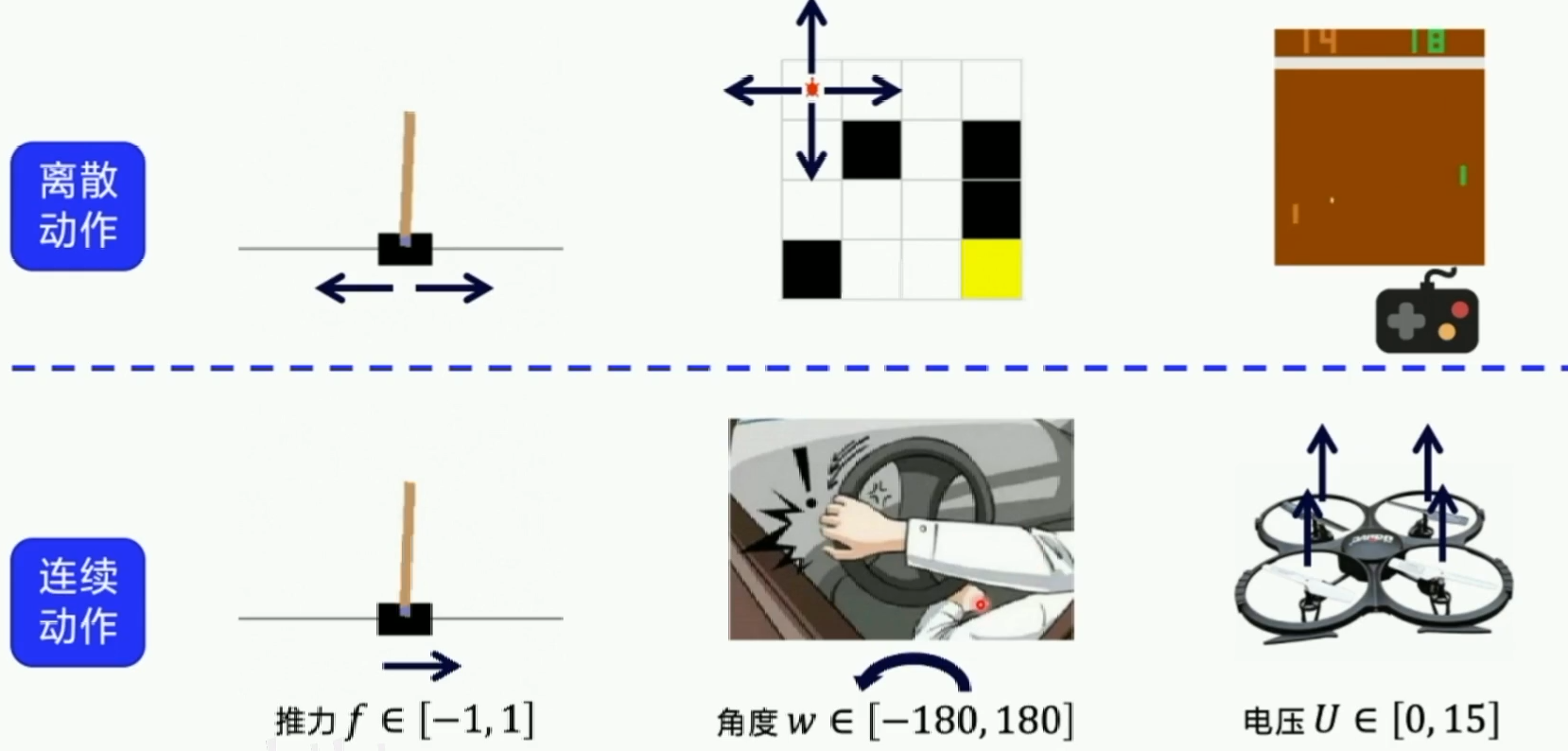
在连续动作空间的求解中,前面讲的Sarsa,DQN,Q-learning,Reinforce都是没有办法处理的。这时候我们就需要用神经网络的输出代表一个动作的“幅度”,而不是单纯决定做某个动作。例如我们可以用一个-1到1的输出来控制小车的速度,正数是前进,负数是后退,绝对值越大速度越快。
DDPG(Deep Deterministic Policy Gradient)
DDPG借鉴了DQN的技巧,也就是目标网络和经验回放。并且可以输出确定的动作(即动作的幅度),并且是一个单步更新的Policy网络。
Actor-Critic
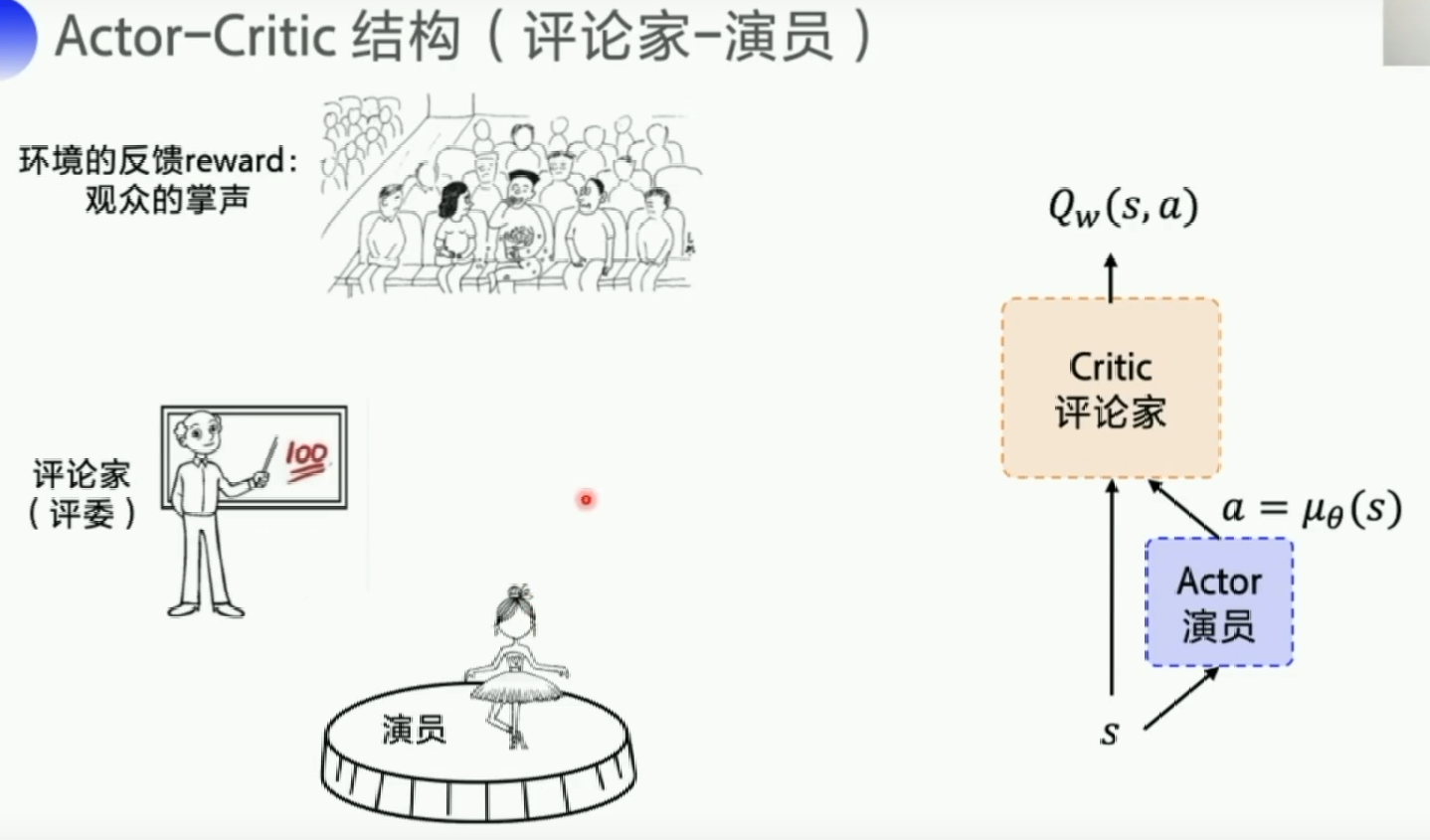
我们有两个神经网络,一个Actor,一个Critic。Actor的任务是对外输出动作并且根据Critic的打分来调整自己的参数来获得更好的输出,使得Critic打分更高。
Critic的任务是对Actor的输出做评估(预测),并且通过reward不断调整自己的预测能可能地接近reward。这也就是一个Q网络。
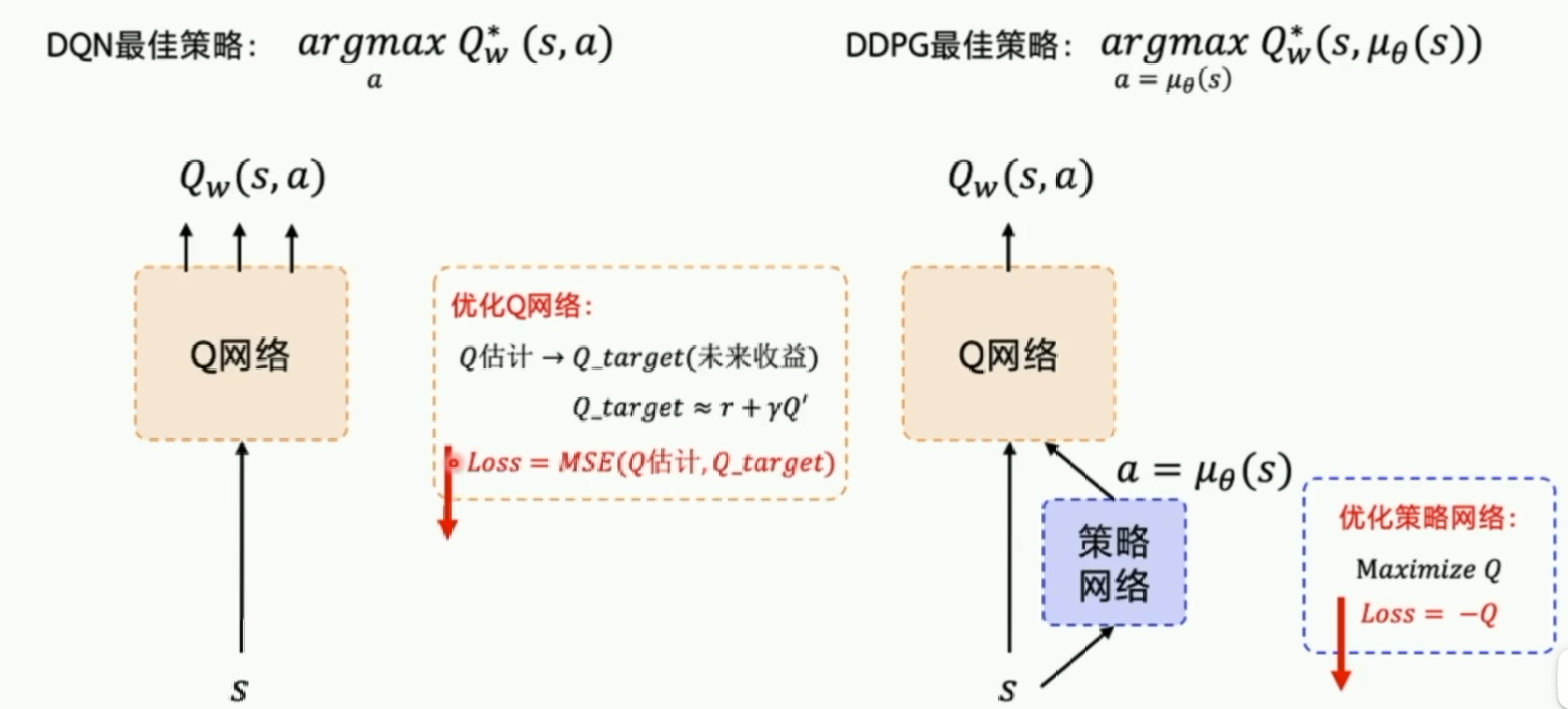
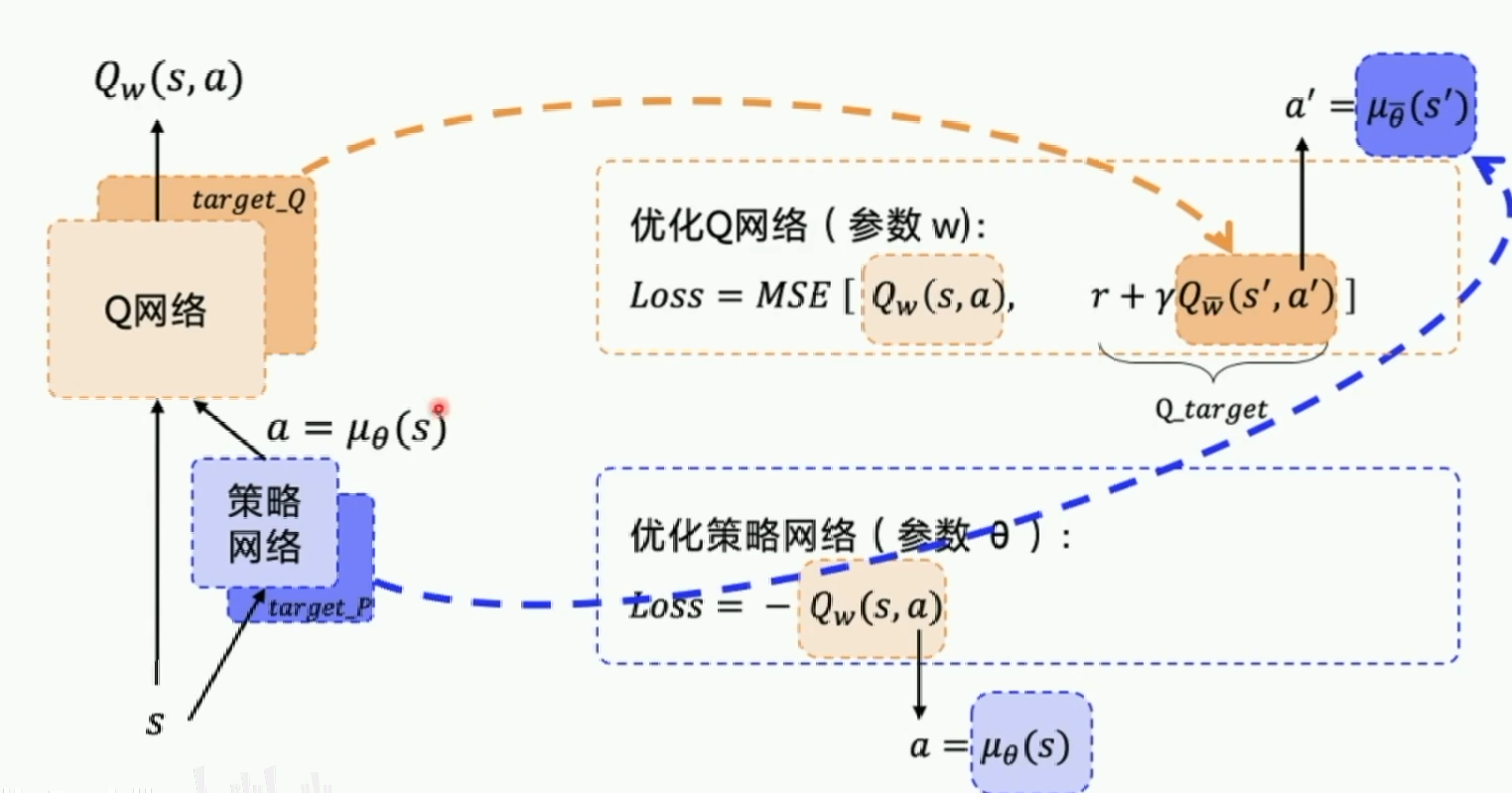
实际上,为了更新的稳定,我们又分别给Actor和Critic都附加一个Target网络,和DQN一样,也就是说DDPG存在四个网络。
代码实现
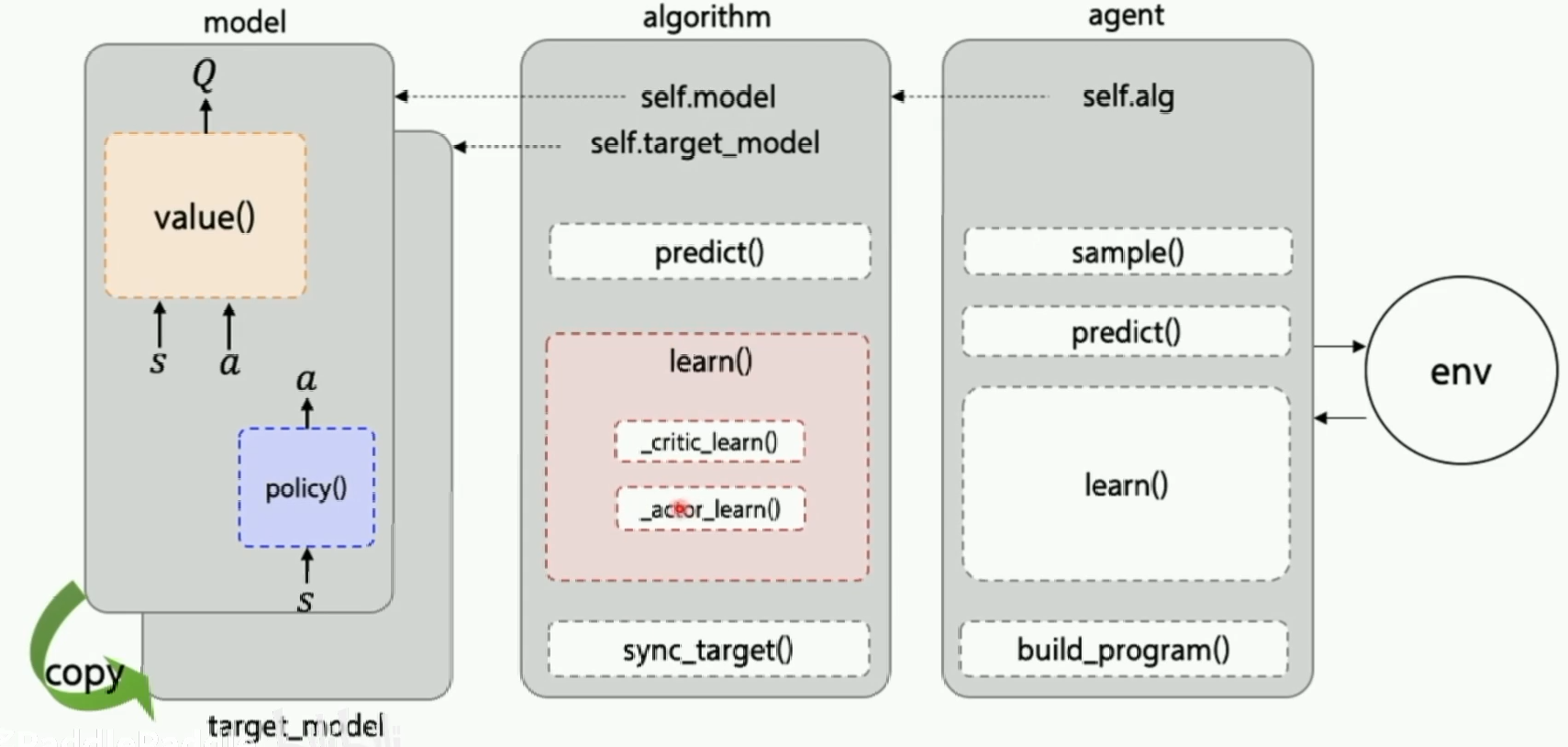
分类数据的reply_memory.py:
import random
import collections
import numpy as np
class ReplayMemory(object):
def __init__(self, max_size):
self.buffer = collections.deque(maxlen=max_size)
def append(self, exp):
self.buffer.append(exp)
def sample(self, batch_size):
mini_batch = random.sample(self.buffer, batch_size)
obs_batch, action_batch, reward_batch, next_obs_batch, done_batch = [], [], [], [], []
for experience in mini_batch:
s, a, r, s_p, done = experience
obs_batch.append(s)
action_batch.append(a)
reward_batch.append(r)
next_obs_batch.append(s_p)
done_batch.append(done)
return np.array(obs_batch).astype('float32'), \
np.array(action_batch).astype('float32'), np.array(reward_batch).astype('float32'),\
np.array(next_obs_batch).astype('float32'), np.array(done_batch).astype('float32')
def __len__(self):
return len(self.buffer)model.py:
import parl
from parl import layers
# 用一个类把两个模型封装起来
class Model(parl.Model):
def __init__(self, act_dim):
self.actor_model = ActorModel(act_dim)
self.critic_model = CriticModel()
def policy(self, obs):
return self.actor_model.policy(obs)
def value(self, obs, act):
return self.critic_model.value(obs, act)
# 获取actor网络的parameters的名称,返回包含模型所有参数名称的list
def get_actor_params(self):
return self.actor_model.parameters()
# Actor网络
class ActorModel(parl.Model):
def __init__(self, act_dim):
hid_size = 100
self.fc1 = layers.fc(size=hid_size, act='relu')
self.fc2 = layers.fc(size=act_dim, act='tanh')
def policy(self, obs):
hid = self.fc1(obs)
means = self.fc2(hid)
return means
# Critic网络
class CriticModel(parl.Model):
def __init__(self):
hid_size = 100
self.fc1 = layers.fc(size=hid_size, act='relu')
self.fc2 = layers.fc(size=1, act=None)
def value(self, obs, act):
# 拼接两个数组
concat = layers.concat([obs, act], axis=1)
hid = self.fc1(concat)
Q = self.fc2(hid)
Q = layers.squeeze(Q, axes=[1])
return Q
最关键的algorithm.py:
其实两个Target model都是给Critic更新参数用的,而Actor更新参数只需要看Critic的输出。
import parl
from parl import layers
from copy import deepcopy
from paddle import fluid
class DDPG(parl.Algorithm):
def __init__(self,model,gamma=None,tau=None,actor_lr=None,critic_lr=None):
""" DDPG algorithm
Args:
model (parl.Model): actor and critic 的前向网络.
model 必须实现 get_actor_params() 方法.
gamma (float): reward的衰减因子.
tau (float): self.target_model 跟 self.model 同步参数 的 软更新参数
actor_lr (float): actor 的学习率
critic_lr (float): critic 的学习率
"""
assert isinstance(gamma, float)
assert isinstance(tau, float)
assert isinstance(actor_lr, float)
assert isinstance(critic_lr, float)
self.gamma = gamma
self.tau = tau
self.actor_lr = actor_lr
self.critic_lr = critic_lr
self.model = model
self.target_model = deepcopy(model)
def predict(self, obs):
""" 使用 self.model 的 actor model 来预测动作
"""
return self.model.policy(obs)
def learn(self, obs, action, reward, next_obs, terminal):
""" 用DDPG算法更新 actor 和 critic
"""
actor_cost = self._actor_learn(obs)
critic_cost = self._critic_learn(obs, action, reward, next_obs,
terminal)
return actor_cost, critic_cost
def _actor_learn(self, obs):
# 计算Critic中的Q,然后使这个Q越大越好
action = self.model.policy(obs)
Q = self.model.value(obs, action)
cost = layers.reduce_mean(-1.0 * Q)
optimizer = fluid.optimizer.AdamOptimizer(self.actor_lr)
# 只更新Actor的参数,因此要给minimize指定目标,否则也会调整到Critic的参数
optimizer.minimize(cost, parameter_list=self.model.get_actor_params())
return cost
def _critic_learn(self, obs, action, reward, next_obs, terminal):
# 计算Target Q,也就是目标价值
next_action = self.target_model.policy(next_obs)
next_Q = self.target_model.value(next_obs, next_action)
terminal = layers.cast(terminal, dtype='float32')
target_Q = reward + (1.0 - terminal) * self.gamma * next_Q
target_Q.stop_gradient = True
# 根据网络得出现在的Q,然后算出均方差,用来训练网络使得Q趋近于Target Q
Q = self.model.value(obs, action)
cost = layers.square_error_cost(Q, target_Q)
cost = layers.reduce_mean(cost)
optimizer = fluid.optimizer.AdamOptimizer(self.critic_lr)
optimizer.minimize(cost)
return cost
def sync_target(self, decay=None, share_vars_parallel_executor=None):
""" self.target_model从self.model复制参数过来,若decay不为None,则是软更新
"""
if decay is None:
decay = 1.0 - self.tau
self.model.sync_weights_to(
self.target_model,
decay=decay,
share_vars_parallel_executor=share_vars_parallel_executor)
train.py:
import gym
import numpy as np
import parl
from parl.utils import logger
from agent import Agent
from model import Model
from algorithm import DDPG # from parl.algorithms import DDPG
from env import ContinuousCartPoleEnv
from replay_memory import ReplayMemory
ACTOR_LR = 1e-3 # Actor网络的 learning rate
CRITIC_LR = 1e-3 # Critic网络的 learning rate
GAMMA = 0.99 # reward 的衰减因子
TAU = 0.001 # 软更新的系数
MEMORY_SIZE = int(1e6) # 经验池大小
MEMORY_WARMUP_SIZE = MEMORY_SIZE // 20 # 预存一部分经验之后再开始训练
BATCH_SIZE = 128
REWARD_SCALE = 0.1 # reward 缩放系数
NOISE = 0.05 # 动作噪声方差
TRAIN_EPISODE = 6e3 # 训练的总episode数
# 训练一个episode
def run_episode(agent, env, rpm):
obs = env.reset()
total_reward = 0
steps = 0
while True:
steps += 1
batch_obs = np.expand_dims(obs, axis=0)
action = agent.predict(batch_obs.astype('float32'))
# 增加探索扰动, 输出限制在 [-1.0, 1.0] 范围内
action = np.clip(np.random.normal(action, NOISE), -1.0, 1.0)
next_obs, reward, done, info = env.step(action)
action = [action] # 方便存入replaymemory
rpm.append((obs, action, REWARD_SCALE * reward, next_obs, done))
# 预存多个经验以及每五个step提取一次
if len(rpm) > MEMORY_WARMUP_SIZE and (steps % 5) == 0:
(batch_obs, batch_action, batch_reward, batch_next_obs,
batch_done) = rpm.sample(BATCH_SIZE)
agent.learn(batch_obs, batch_action, batch_reward, batch_next_obs,
batch_done)
obs = next_obs
total_reward += reward
if done or steps >= 200:
break
return total_reward
# 评估 agent, 跑 5 个episode,总reward求平均
def evaluate(env, agent, render=False):
eval_reward = []
for i in range(5):
obs = env.reset()
total_reward = 0
steps = 0
while True:
batch_obs = np.expand_dims(obs, axis=0)
action = agent.predict(batch_obs.astype('float32'))
action = np.clip(action, -1.0, 1.0)
steps += 1
next_obs, reward, done, info = env.step(action)
obs = next_obs
total_reward += reward
if render:
env.render()
if done or steps >= 200:
break
eval_reward.append(total_reward)
return np.mean(eval_reward)
def main():
env = ContinuousCartPoleEnv()
obs_dim = env.observation_space.shape[0]
act_dim = env.action_space.shape[0]
# 使用PARL框架创建agent
model = Model(act_dim)
algorithm = DDPG(
model, gamma=GAMMA, tau=TAU, actor_lr=ACTOR_LR, critic_lr=CRITIC_LR)
agent = Agent(algorithm, obs_dim, act_dim)
# 创建经验池
rpm = ReplayMemory(MEMORY_SIZE)
# 往经验池中预存数据
while len(rpm) < MEMORY_WARMUP_SIZE:
run_episode(agent, env, rpm)
episode = 0
while episode < TRAIN_EPISODE:
for i in range(50):
total_reward = run_episode(agent, env, rpm)
episode += 1
# 每50个episode评估一次
eval_reward = evaluate(env, agent, render=False)
logger.info('episode:{} Test reward:{}'.format(
episode, eval_reward))
if __name__ == '__main__':
main()
另外附上环境的代码env.py:
"""
Classic cart-pole system implemented by Rich Sutton et al.
Copied from http://incompleteideas.net/sutton/book/code/pole.c
permalink: https://perma.cc/C9ZM-652R
Continuous version by Ian Danforth
"""
import math
import gym
from gym import spaces, logger
from gym.utils import seeding
import numpy as np
class ContinuousCartPoleEnv(gym.Env):
metadata = {
'render.modes': ['human', 'rgb_array'],
'video.frames_per_second': 50
}
def __init__(self):
self.gravity = 9.8
self.masscart = 1.0
self.masspole = 0.1
self.total_mass = (self.masspole + self.masscart)
self.length = 0.5 # actually half the pole's length
self.polemass_length = (self.masspole * self.length)
self.force_mag = 30.0
self.tau = 0.02 # seconds between state updates
self.min_action = -1.0
self.max_action = 1.0
# Angle at which to fail the episode
self.theta_threshold_radians = 12 * 2 * math.pi / 360
self.x_threshold = 2.4
# Angle limit set to 2 * theta_threshold_radians so failing observation
# is still within bounds
high = np.array([
self.x_threshold * 2,
np.finfo(np.float32).max, self.theta_threshold_radians * 2,
np.finfo(np.float32).max
])
self.action_space = spaces.Box(
low=self.min_action, high=self.max_action, shape=(1, ))
self.observation_space = spaces.Box(-high, high)
self.seed()
self.viewer = None
self.state = None
self.steps_beyond_done = None
def seed(self, seed=None):
self.np_random, seed = seeding.np_random(seed)
return [seed]
def stepPhysics(self, force):
x, x_dot, theta, theta_dot = self.state
costheta = math.cos(theta)
sintheta = math.sin(theta)
temp = (force + self.polemass_length * theta_dot * theta_dot * sintheta
) / self.total_mass
thetaacc = (self.gravity * sintheta - costheta * temp) / \
(self.length * (4.0/3.0 - self.masspole * costheta * costheta / self.total_mass))
xacc = temp - self.polemass_length * thetaacc * costheta / self.total_mass
x = x + self.tau * x_dot
x_dot = x_dot + self.tau * xacc
theta = theta + self.tau * theta_dot
theta_dot = theta_dot + self.tau * thetaacc
return (x, x_dot, theta, theta_dot)
def step(self, action):
action = np.expand_dims(action, 0)
assert self.action_space.contains(action), \
"%r (%s) invalid" % (action, type(action))
# Cast action to float to strip np trappings
force = self.force_mag * float(action)
self.state = self.stepPhysics(force)
x, x_dot, theta, theta_dot = self.state
done = x < -self.x_threshold \
or x > self.x_threshold \
or theta < -self.theta_threshold_radians \
or theta > self.theta_threshold_radians
done = bool(done)
if not done:
reward = 1.0
elif self.steps_beyond_done is None:
# Pole just fell!
self.steps_beyond_done = 0
reward = 1.0
else:
if self.steps_beyond_done == 0:
logger.warn("""
You are calling 'step()' even though this environment has already returned
done = True. You should always call 'reset()' once you receive 'done = True'
Any further steps are undefined behavior.
""")
self.steps_beyond_done += 1
reward = 0.0
return np.array(self.state), reward, done, {}
def reset(self):
self.state = self.np_random.uniform(low=-0.05, high=0.05, size=(4, ))
self.steps_beyond_done = None
return np.array(self.state)
def render(self, mode='human'):
screen_width = 600
screen_height = 400
world_width = self.x_threshold * 2
scale = screen_width / world_width
carty = 100 # TOP OF CART
polewidth = 10.0
polelen = scale * 1.0
cartwidth = 50.0
cartheight = 30.0
if self.viewer is None:
from gym.envs.classic_control import rendering
self.viewer = rendering.Viewer(screen_width, screen_height)
l, r, t, b = -cartwidth / 2, cartwidth / 2, cartheight / 2, -cartheight / 2
axleoffset = cartheight / 4.0
cart = rendering.FilledPolygon([(l, b), (l, t), (r, t), (r, b)])
self.carttrans = rendering.Transform()
cart.add_attr(self.carttrans)
self.viewer.add_geom(cart)
l, r, t, b = -polewidth / 2, polewidth / 2, polelen - polewidth / 2, -polewidth / 2
pole = rendering.FilledPolygon([(l, b), (l, t), (r, t), (r, b)])
pole.set_color(.8, .6, .4)
self.poletrans = rendering.Transform(translation=(0, axleoffset))
pole.add_attr(self.poletrans)
pole.add_attr(self.carttrans)
self.viewer.add_geom(pole)
self.axle = rendering.make_circle(polewidth / 2)
self.axle.add_attr(self.poletrans)
self.axle.add_attr(self.carttrans)
self.axle.set_color(.5, .5, .8)
self.viewer.add_geom(self.axle)
self.track = rendering.Line((0, carty), (screen_width, carty))
self.track.set_color(0, 0, 0)
self.viewer.add_geom(self.track)
if self.state is None:
return None
x = self.state
cartx = x[0] * scale + screen_width / 2.0 # MIDDLE OF CART
self.carttrans.set_translation(cartx, carty)
self.poletrans.set_rotation(-x[2])
return self.viewer.render(return_rgb_array=(mode == 'rgb_array'))
def close(self):
if self.viewer:
self.viewer.close()
拓展
RLSchool:一个强化学习模拟环境合集

无人机悬浮控制任务


更多环境



1星环境:简单的弹跳和接球游戏:https://github.com/shivaverma/Orbit
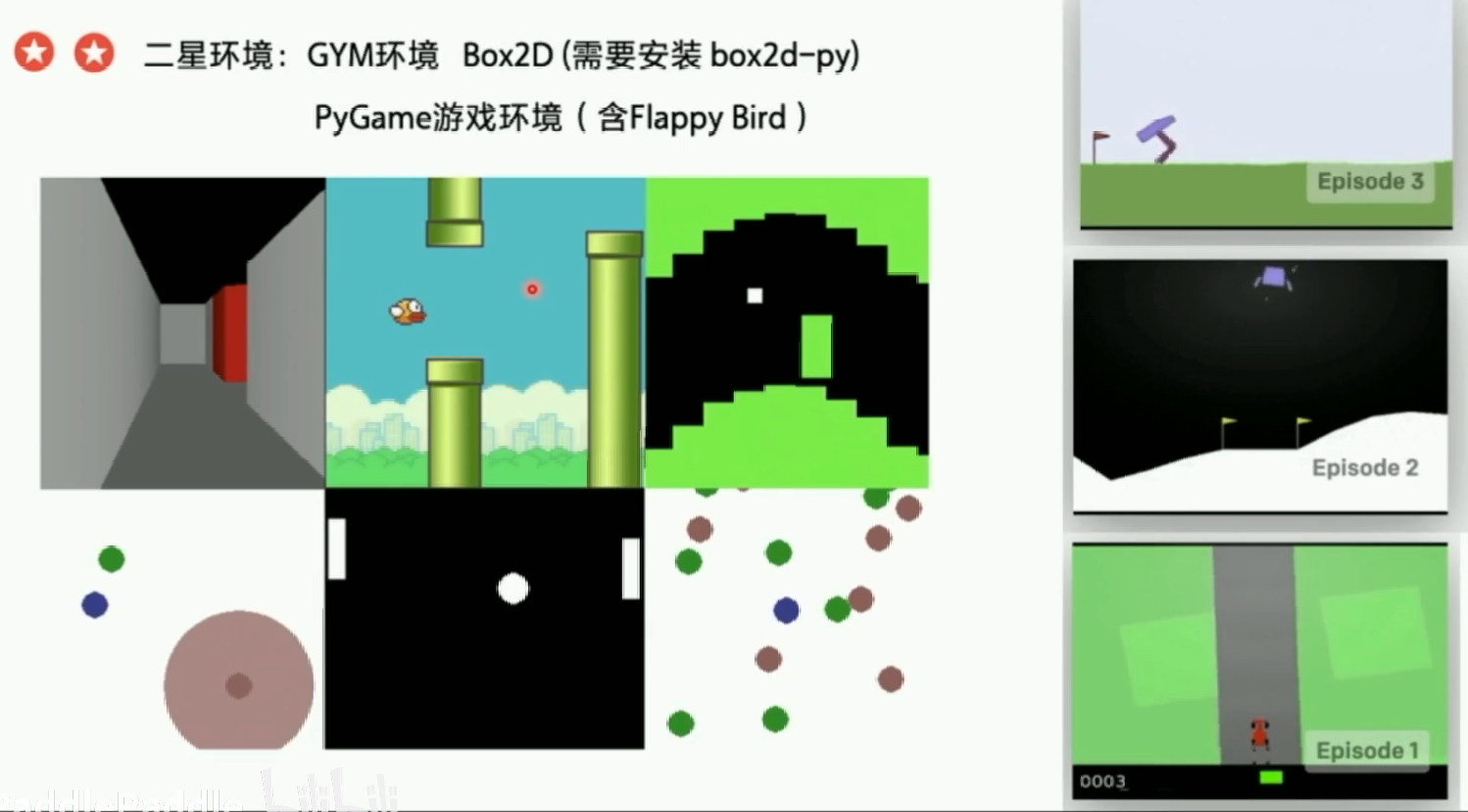
2星环境:GYM环境 Box2D (需要安装 box2d-py):https://gym.openai.com/envs/#box2d
PyGame游戏环境(含Flappy Bird):https://github.com/ntasfi/PyGame-Learning-Environment
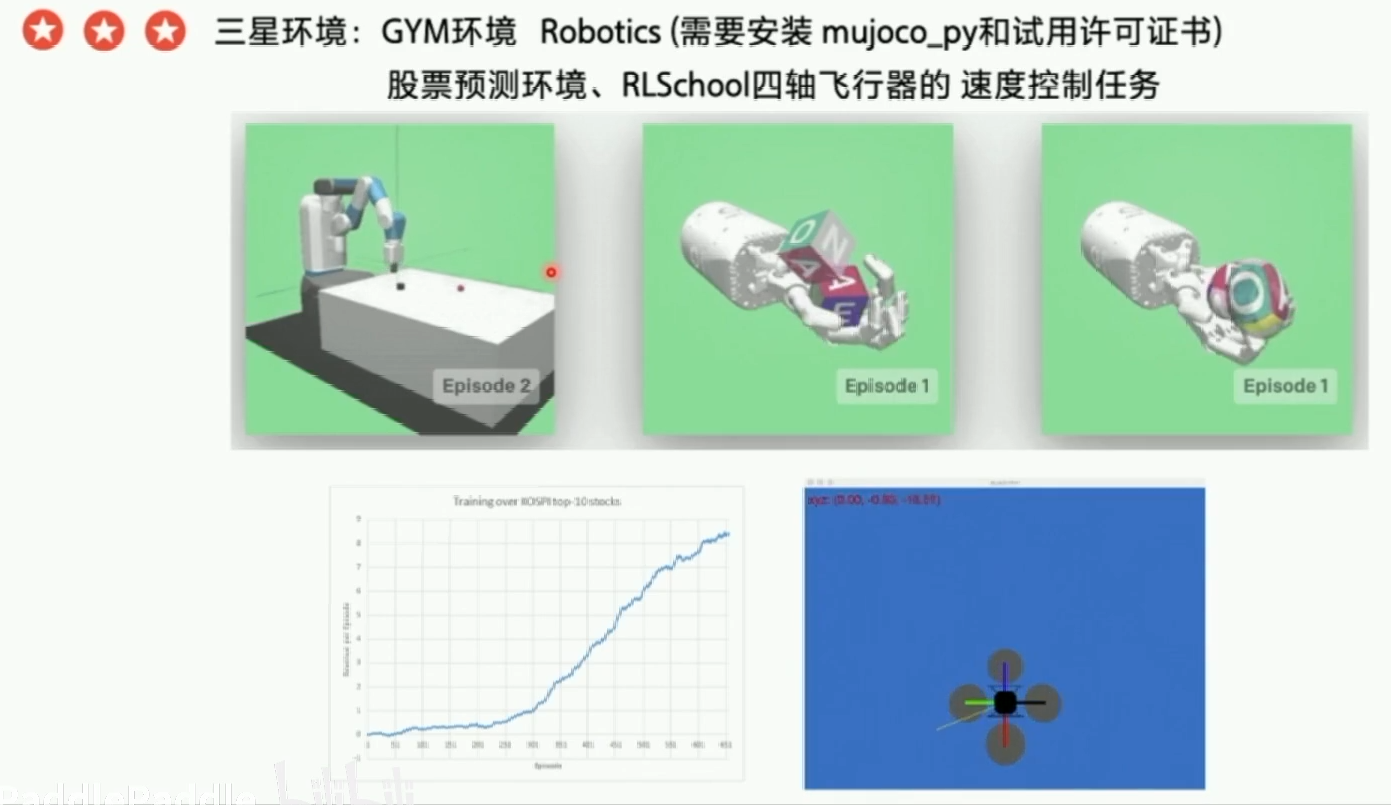
3星环境:GYM环境 Robotics (需要安装 mujoco_py和试用许可证书):https://gym.openai.com/envs/#robotics
股票预测环境:https://github.com/kh-kim/stock_market_reinforcement_learning
RLSchool四轴飞行器的 速度控制任务 “velocity_control”:https://github.com/PaddlePaddle/RLSchool/tree/master/rlschool/quadrotor
4星环境:RLBench任务环境(使用机械臂完成某一项任务):https://github.com/stepjam/RLBench
5星环境:交通信号灯控制:https://github.com/Ujwal2910/Smart-Traffic-Signals-in-India-using-Deep-Reinforcement-Learning-and-Advanced-Computer-Vision



