原课程网址:https://www.bilibili.com/video/BV1Wv411h7kN?p=1
本课程专注于深度学习。
机器学习基本概念
机器学习的本质是找到一个对应的函数。例如声音辨识,输入是声音,输出是文字,这种输入是非常复制的,无法用手写的方法表达,需要借助机器的力量。又如AlphaGo本质也是一个函数,输入是棋盘所有子的位置,输出是下一步落子的位置。
如果一个函数的输出是一个数值,找这个函数的任务叫回归(regression)。
如果给几个选项,让函数的输出选择几个选项,那么这种方法叫分类(classfication)。
如果机器学习要产生一个有结构的物件,例如画图,学文章,就是让机器学会创造(Structured Learning)
找函数的步骤
首先需要一个猜测,这个猜测是建立在对其模型有一定程度上的了解的基础上的,然后再去计算其中的参数。然后用这个模型计算的结果和实际值对比,算出差距e,差距越大效果越差。衡量这种差距的函数叫做Loss:
$$
L = \frac{1}{N}\sum e_n
$$
其中e可以取$|y-\hat{y}|$,也可以取$(y-\hat{y})^2$。
可以根据不同的参数制作出关于Loss的等高线图来观察哪个参数的效果最好,这种图叫做Error Surface:
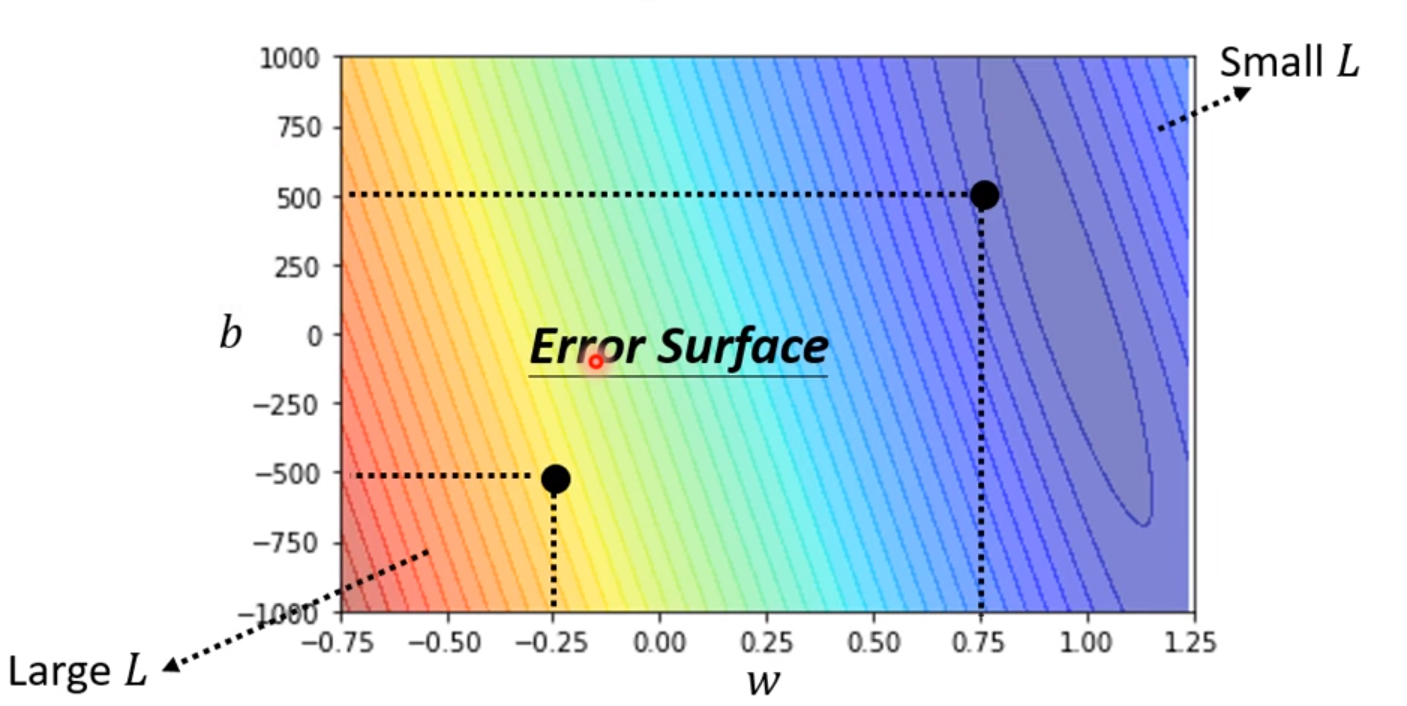
然后我们要做的第三部是最优化的过程,任务是把使得Loss最小的参数找出来。在这门课中唯一用到的方法是梯度递减(Gradient Descent)。
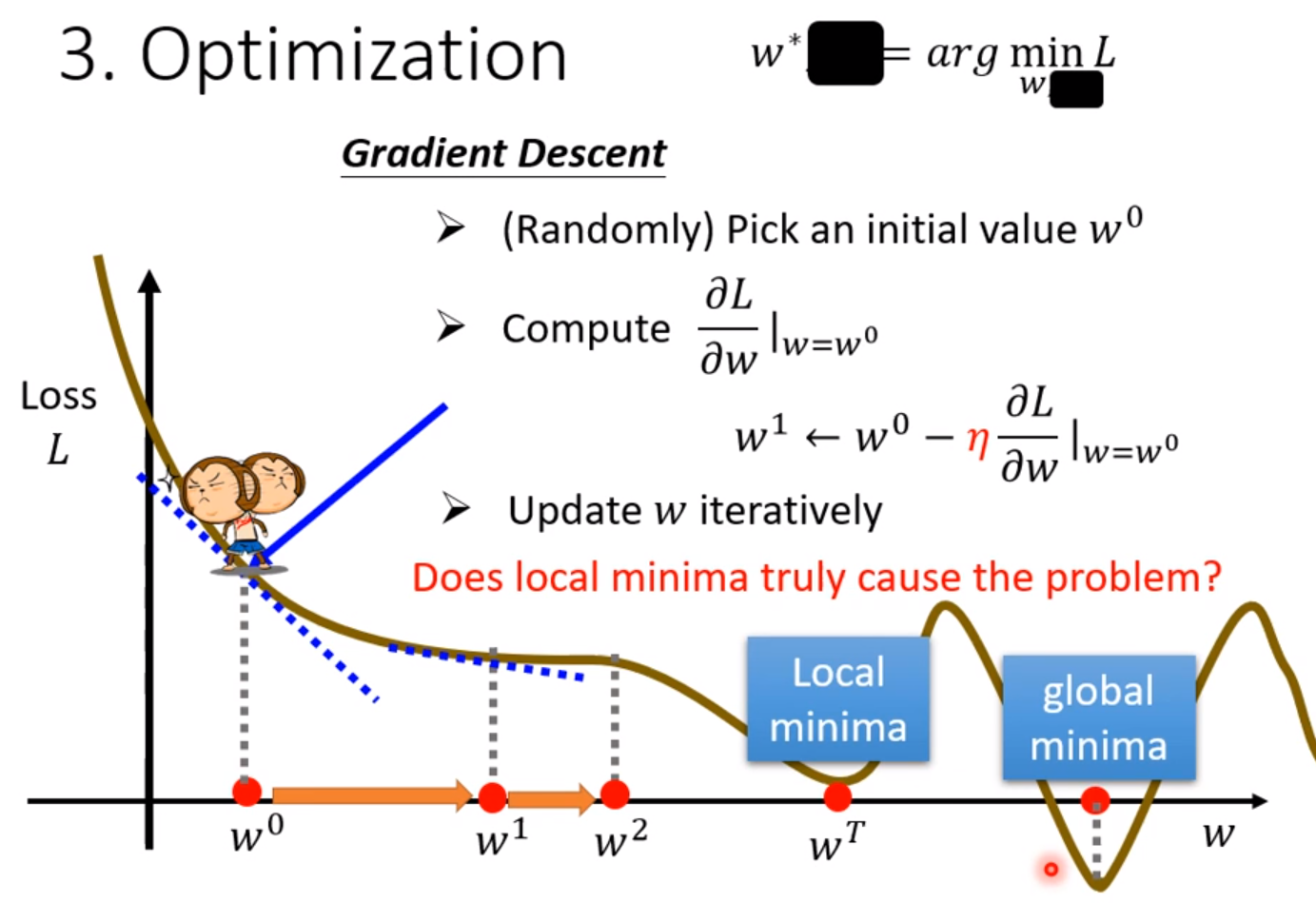
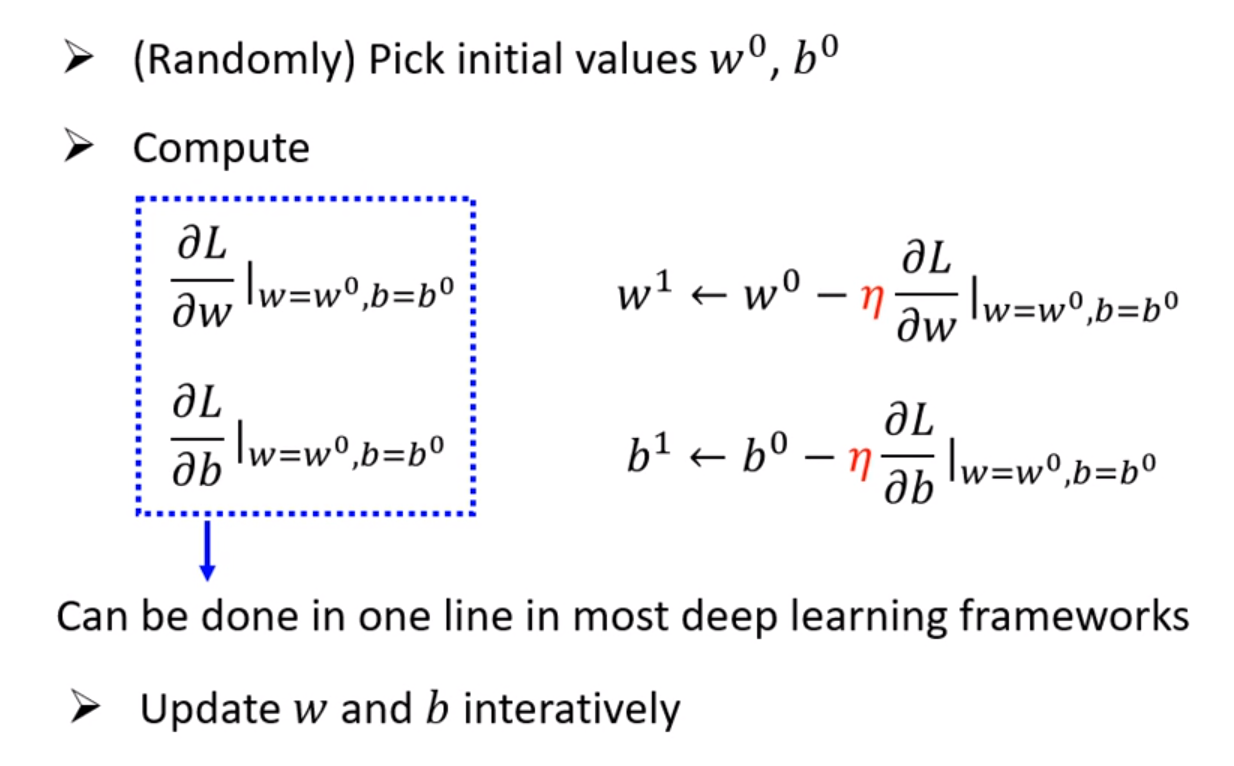
梯度递减的方法是先让Loss函数对参数求导,这个导数为正时,我们就让这个参数减小一定数值,反之增大,导数越大其变化幅度也就越大,这个变换还要乘上我们自己设定的学习率。这样Loss每一步都会随之减小。但是缺点是只能找到局部最优解(local minima),而不一定找到全局最优解(global minima)。
这三个步骤合起来称为训练,是在已知数据的基础上进行的拟合,目标是用这个拟合的函数去预测不知道的数据。
深度学习基本概念
通过对模型运行结果的观察,我们对事物规律会越发了解,这时,我们就有必要更换模型来达到更准确的预测值。而上面用到的都是线性模型(Linear Model),都是权重(weight)乘以已知数据相加,然后再加上偏置值(bias)。这种拟合存在一定局限性(Model Bias)。没有办法模拟很多非线性的真实情况。
但是,一些折线都可以用常数项加上若干的线性函数组成。
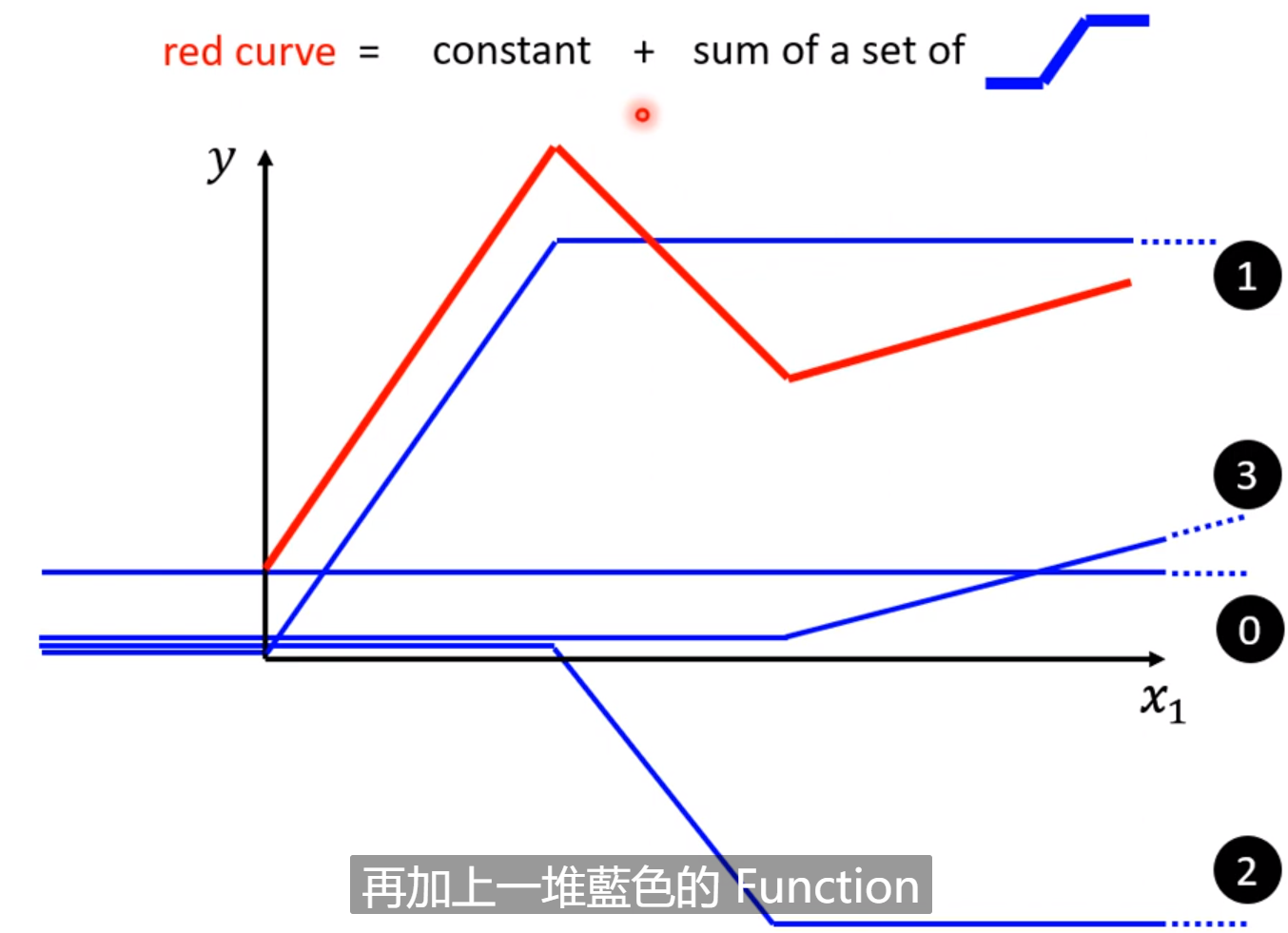
对于曲线也可以用若干的直线去逼近它:
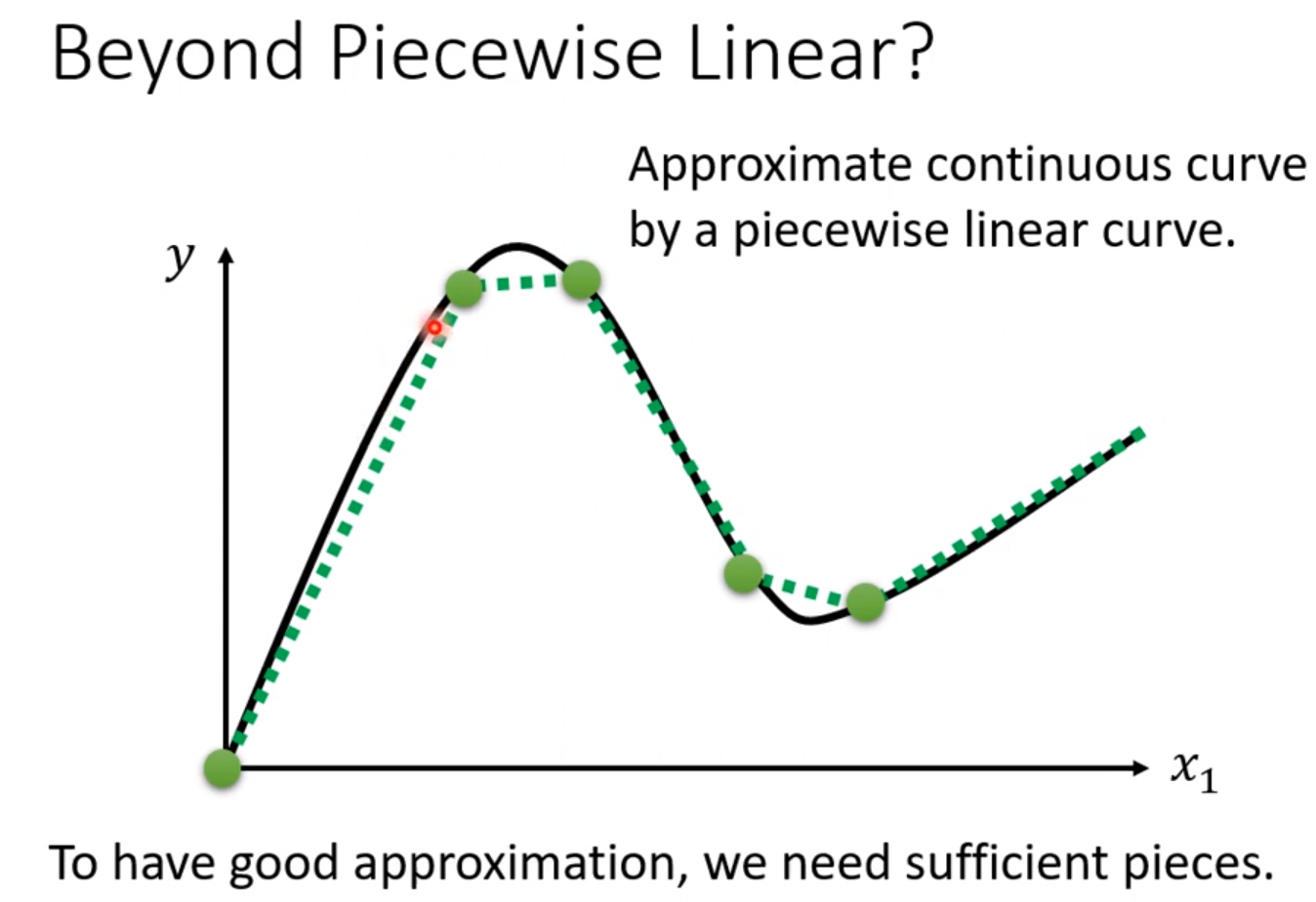
这些若干的函数可以用SIgmoid函数代替,通过调整不同的c,b,w的数值,就可以实现各种各样的sigmoid函数:
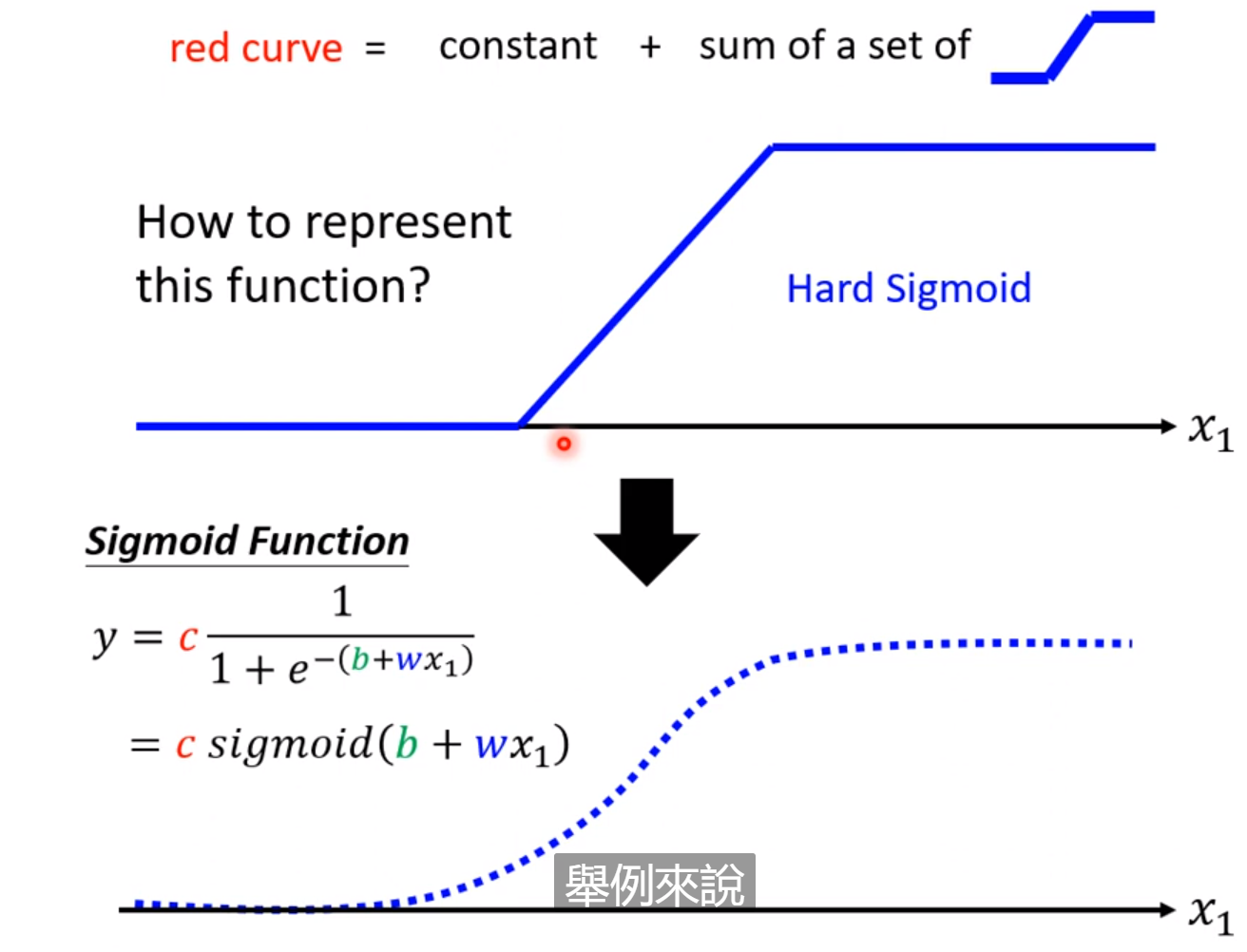
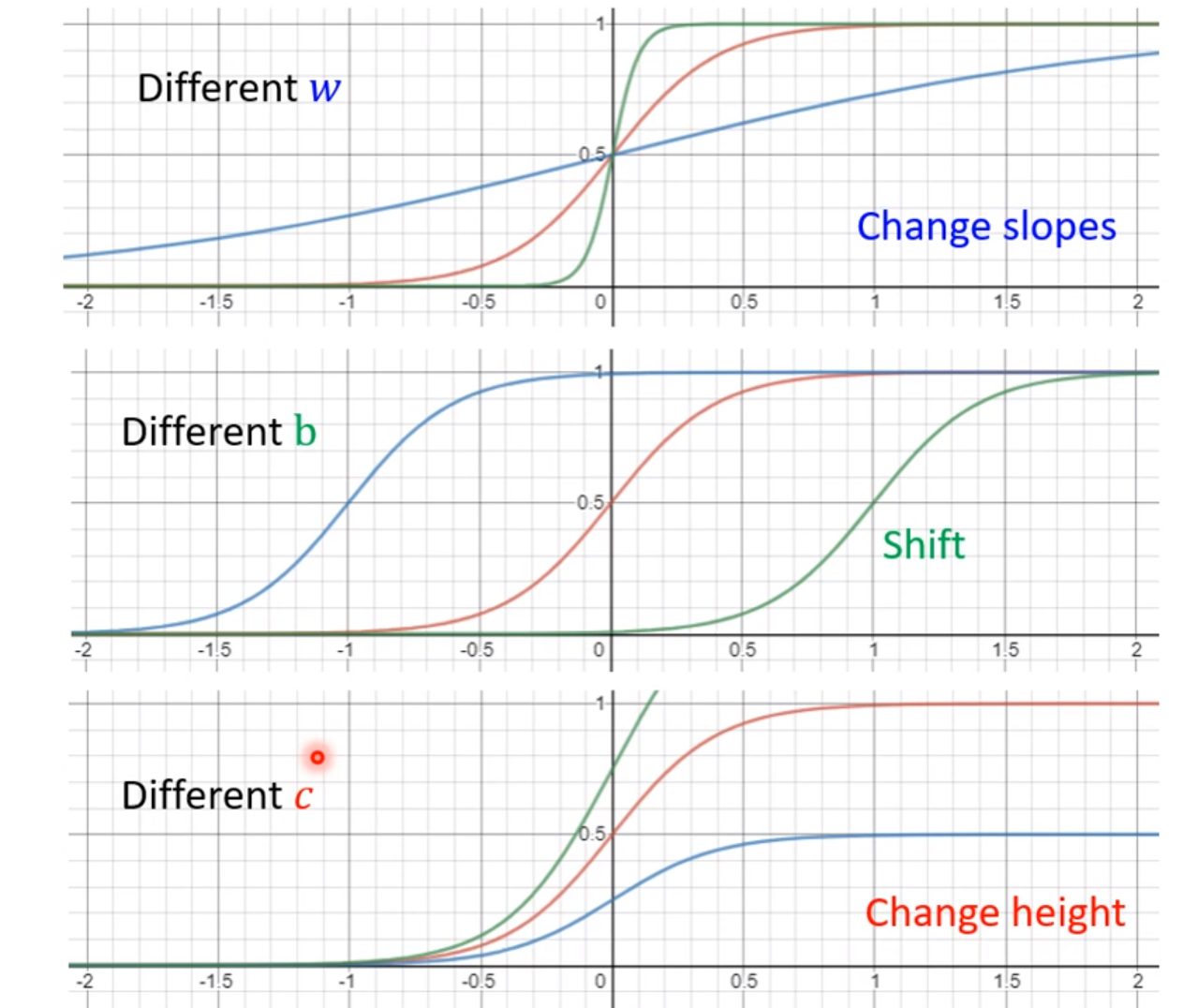
改变w可以改变sigmoid函数的倾斜程度,改变b可以使其左右移动,改变c可以改变其最终高度以及倾斜度。一系列这种函数的加和,就可以很好拟合出任意的函数:
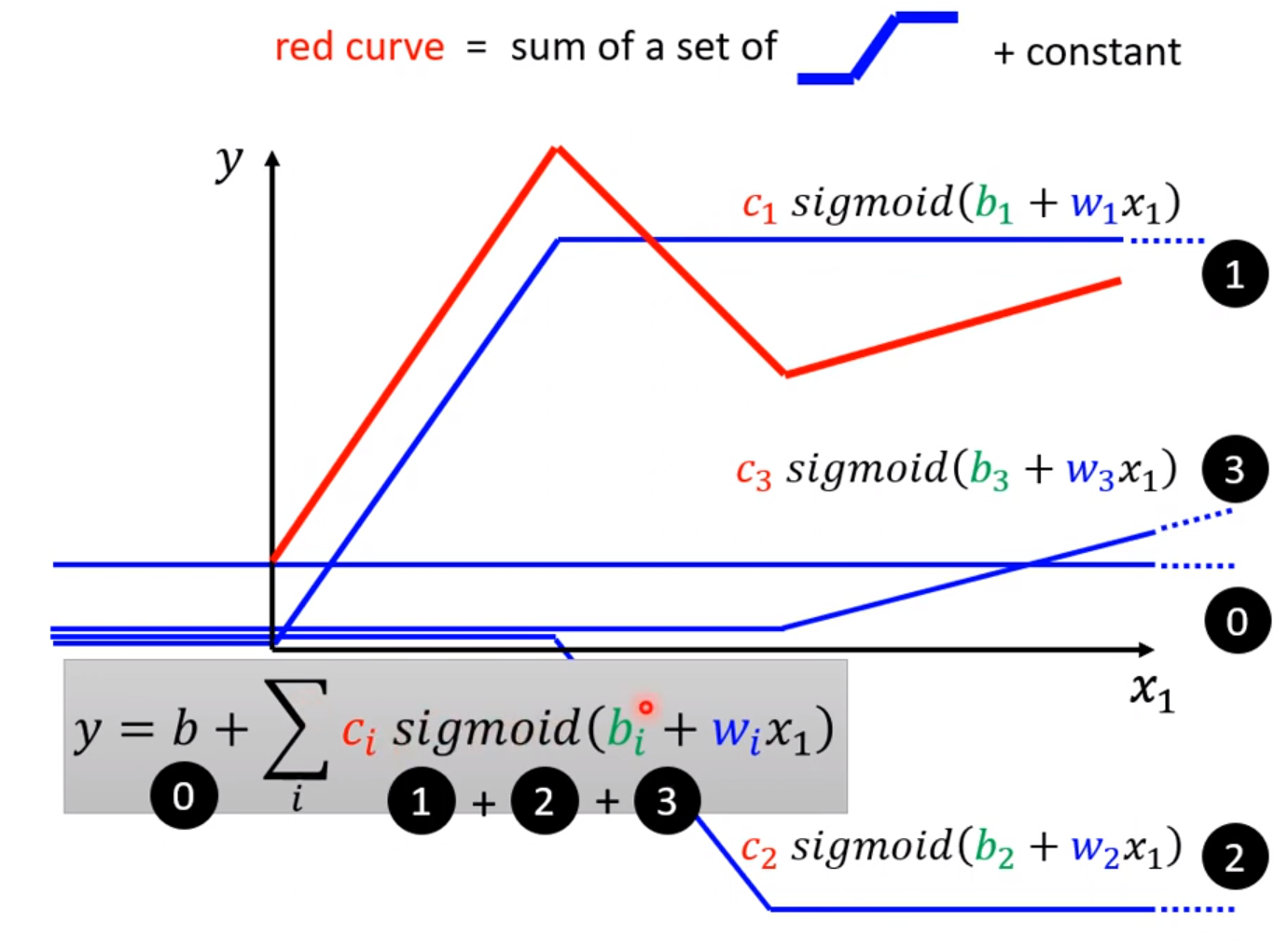
当系统大于一维的情况同理,只是不能用平面表示而已,这样由原来的线性拟合
$$
y= b+ \sum_jw_jx_j
$$
变成了:
$$
y= b + \sum c_i sigmoid(b_i + \sum_j w_{ij}x_j)
$$
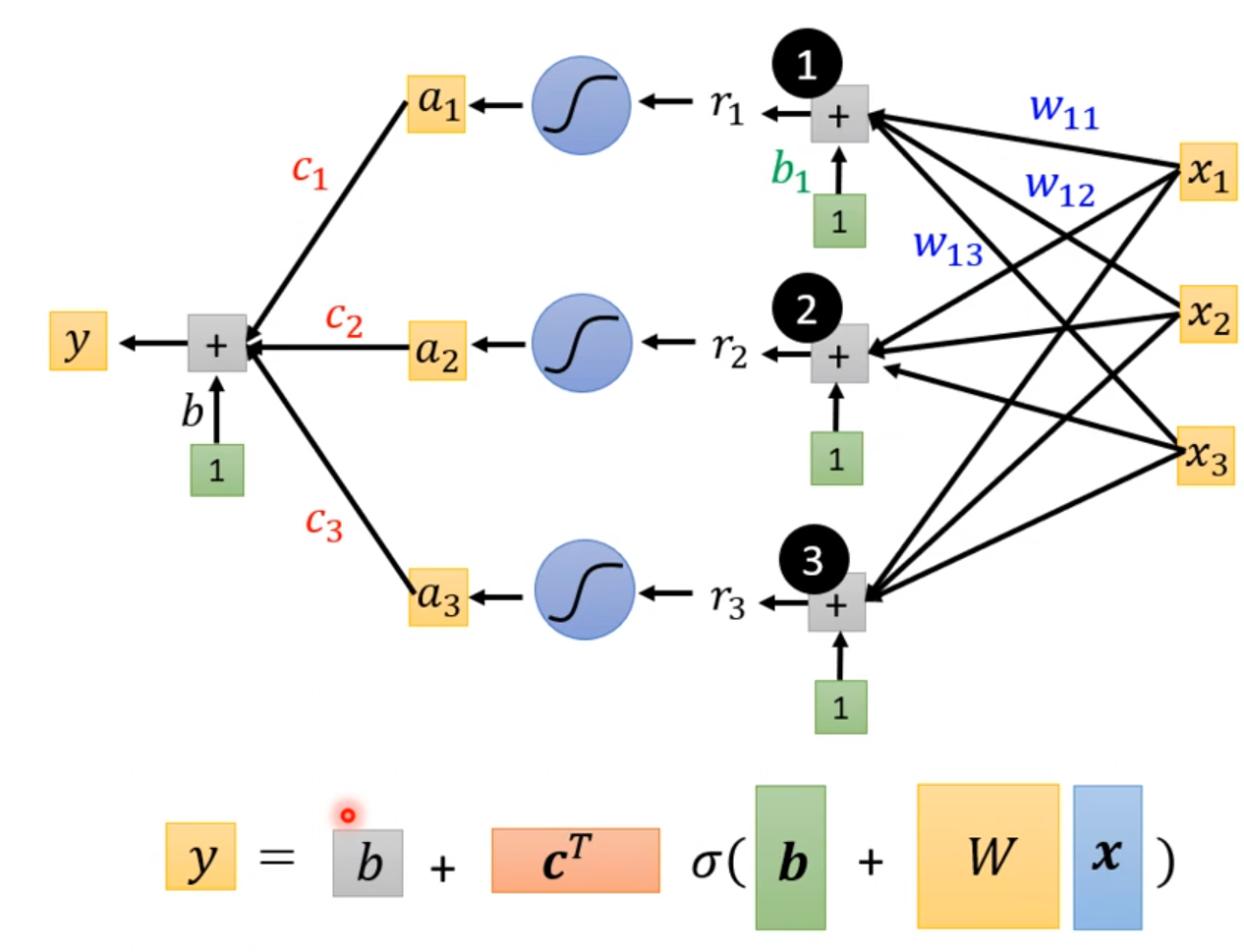
这个函数比较准确地拟合出多维输入的情况下的各种变换了。这个式子是神经网络的基础:
$$
y = b + c^T \sigma(b + Wx)
$$
其中里面所有自己定义的参数拿出来拼成一个很长的向量叫做θ。这样需要设定的参数会比原来的线性拟合多得多,这样我们的目标变成了,找到这么一个θ向量,使得Loss的值最小。
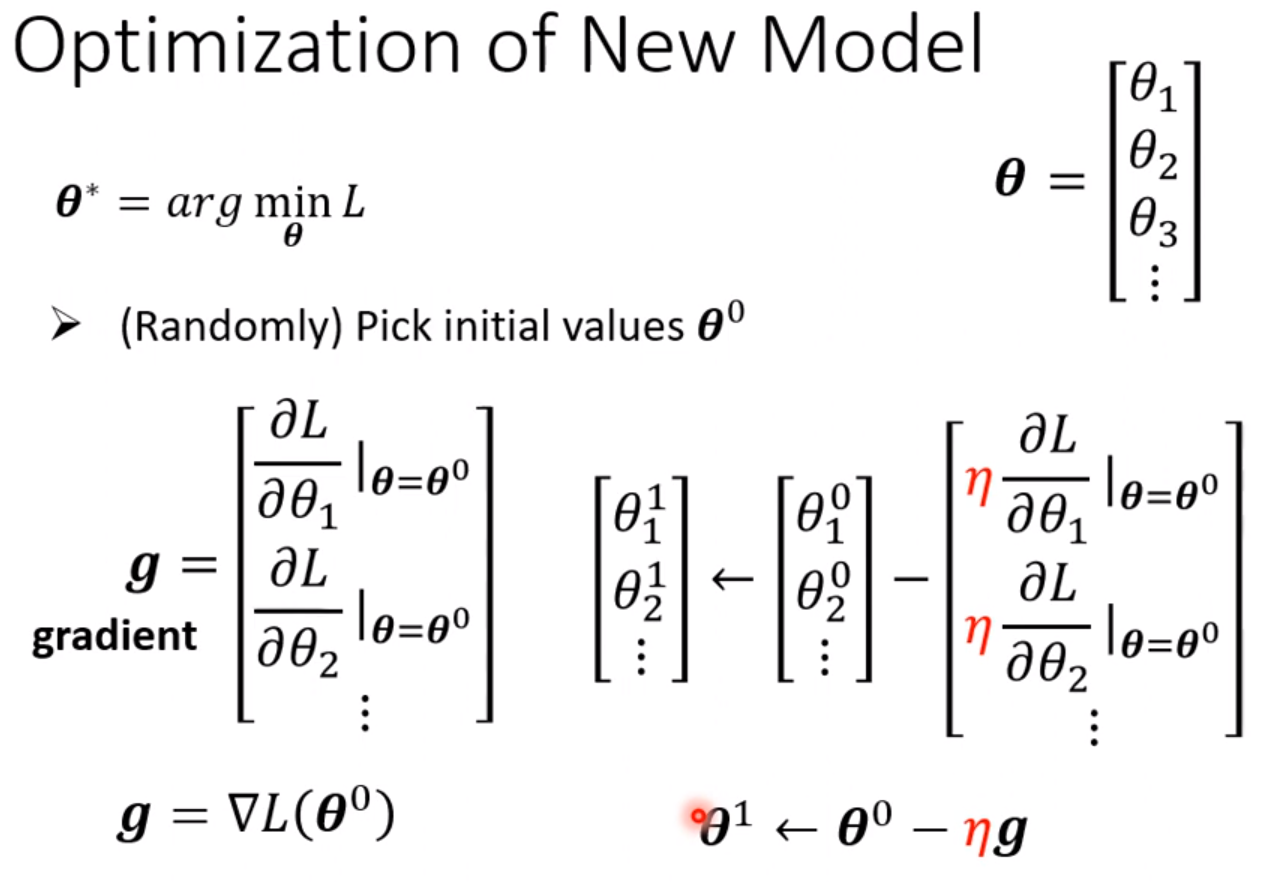
同样最优化的过程和线性拟合的方法一样,采用梯度下降法,不断更新参数,最终得到一个最优解。
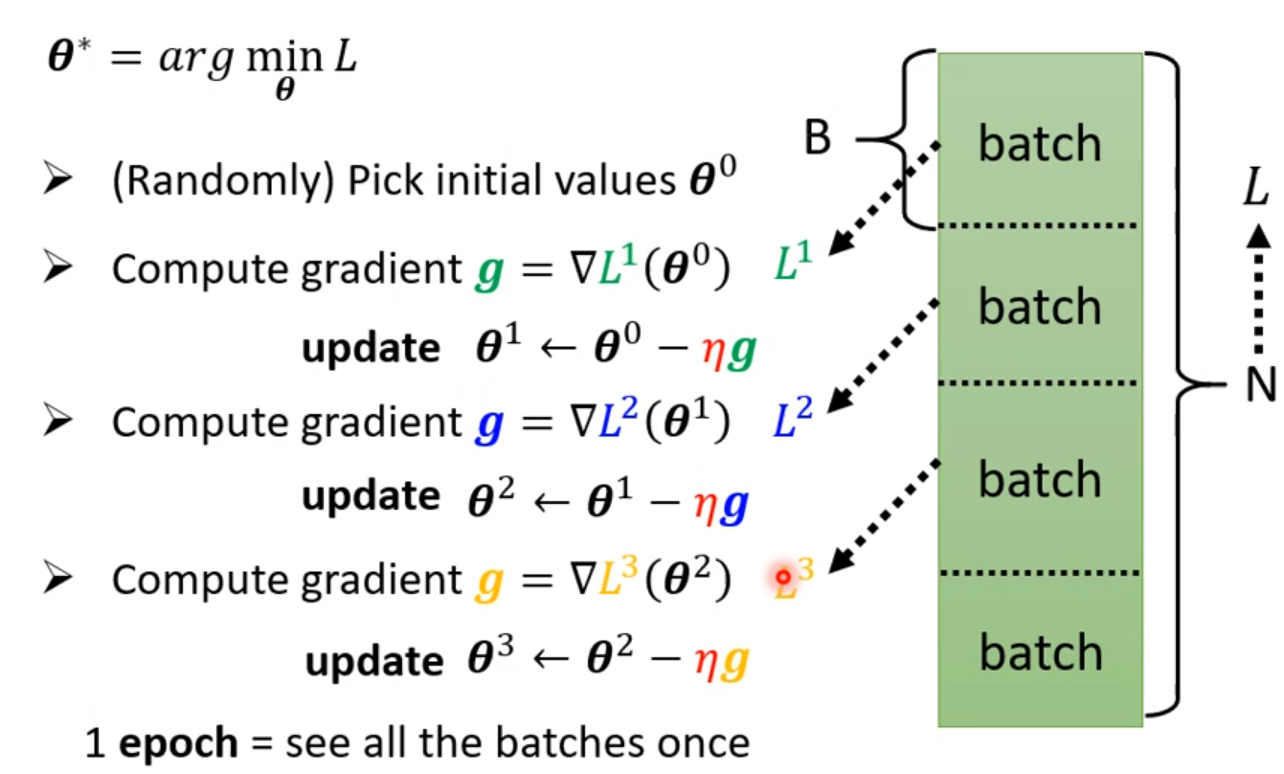
但是在实际操作时,可以对所有的数据进行分组,每次操作一组数据。每次用一组数据算loss进行参数的更新,称为一个update。当所有的数据都进行过一次更新时,称为一个epoch。此处运用的是随机梯度下降的算法。
如果我们不用Sigmoid函数,也可以直接使用专注分明的函数,我们称为ReLU(Rectified Linear Unit)。一个sigmoid要替换成两个ReLU才能做到一样的事情。
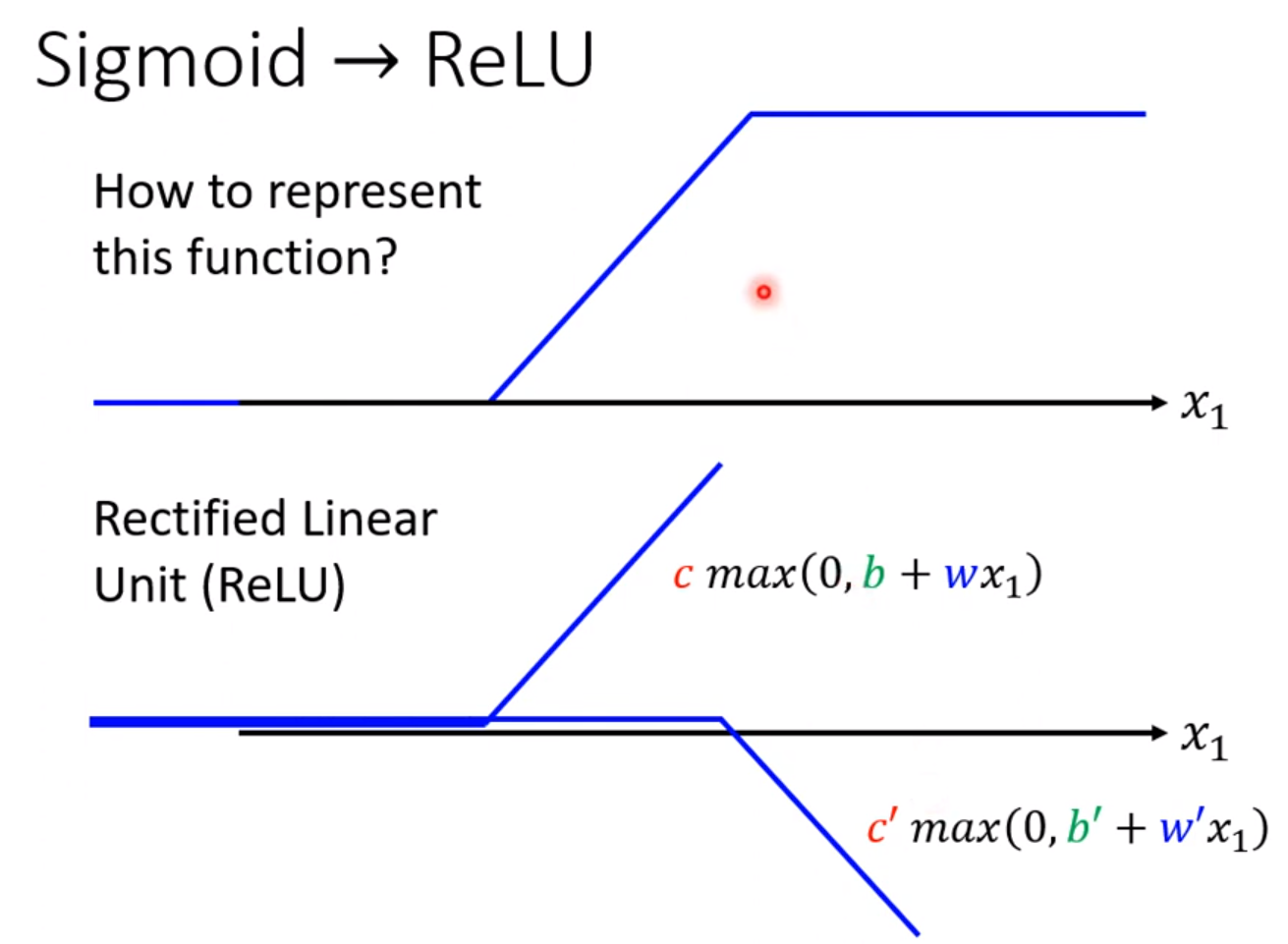
式子变成
$$
y = b + \sum_{2i} c_i max(0,b_i+ \sum_j w_{ij}x_j)
$$
这里max和Sigmoid都称为激活函数(Activation Funcion)。接下来的实验都使用了ReLU,后面会解释为什么选择这种。
我们可以继续改进模型。当我们把上面得出来的数据再进行同样形式的运算,具体做多少次取决于自己,第二层的参数又是于第一层完全不同的,这就是含有隐藏层的神经网络。层数越多,神经网络就越复杂,往往也能实现更多地逻辑,会得模型准确率提高,但是也会有过拟合的问题,注意层数要适当。
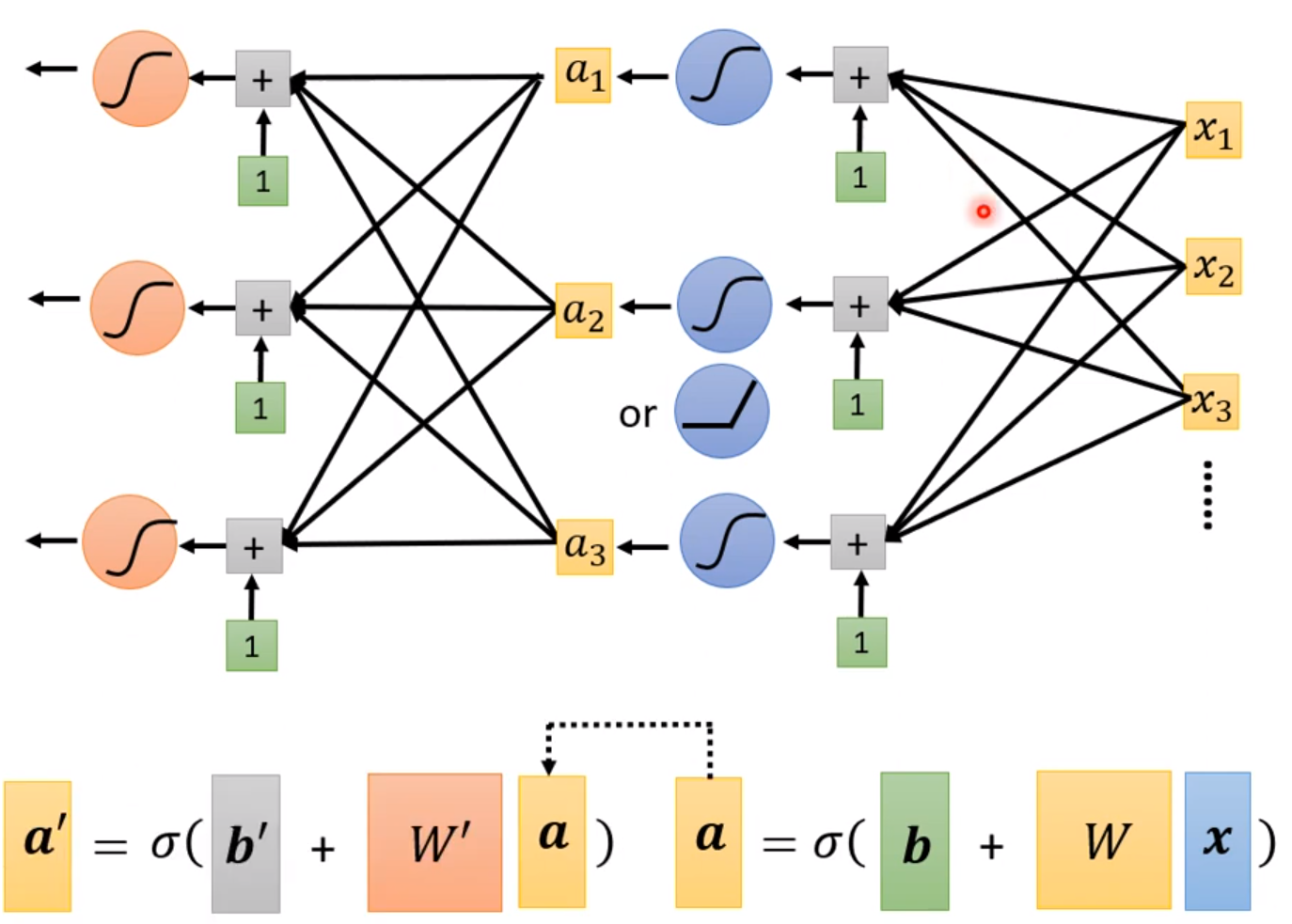
这一套基于神经网络的技术,我们称为深度学习。
反向传播(Backpropagation)
参考视频:https://www.youtube.com/watch?v=ibJpTrp5mcE&ab_channel=Hung-yiLee
可参考另一篇文章《Python神经网络编程》
误差反向传播的方法是使用梯度下降法,即需要求总误差对一个权值的导数。当所在权值在输出层之前,那么:
$$
\frac{dE}{dw_{jk}} = - (t_k - o_k) * sigmoid(\sum_j w_{jk}o_j)(1-sigmoid(\sum_j w_{jk}o_j)) * o_j
$$
其中$t_k$为该权重对应输出节点的真实值,$o_k$为现在该输出节点预测值,$o_j$是隐藏层的输出值。更新权重为
$$
\Delta w_{jk} = \alpha * \frac{dE}{dw_{jk}}
$$
如果是更加前面层级的权重,更新方法为:先通过后面的层级一直往前推算,算出该权重后的一个节点的隐藏层误差,而这个误差的计算可以直接忽略激活函数,直接按照后面的权值的比例进行计算即可。然后再运用上面的公式。当然也可以运用链式法则不断的向前递推来算梯度,计算量会大一些。
随机梯度下降
损失函数不计算全部样本的,而是每次随机找一个样本计算。这个方法在更新的过程中有可能跨过鞍点到达全集最优,因此在神经网络中证明非常有效。但是由于每次只能计算一个样本,因此时间复杂度太高。因此我们在实际运用中取随机梯度下降的算法的时候,我们将两者结合,把样本分成一个个batch,分批进行训练。
Google Colab
请参考我的另一篇文章《Google-Colab及其使用》。
Pytorch教学
这部分内容请务必参考我的另一篇文章《Pytorch教学及示例》。这篇文章不仅详细讲解了Pytorch的用法和手把手的实战教学,还浅显易懂的讲解了各种基础的深度学习模型,相信对你有很大帮助。
作业一
请查看我的另一篇文章《用神经网络预测新冠确诊率》。
训练注意事项
在训练的时候要记住,务必不要用测试集的结果来调节你的模型,过多地根据测试集来调节模型会因为过拟合的问题,在测试集上表现好了,但是在应用的时候表现很差。因此在训练的时候我们不要让测试集进行参与,一般我们把训练集分成两部分,一部分用来训练,一部分用来验证,这时候我们可以用N折交叉验证的方法(N-fold Cross Validation)。先把训练集三等分,三分之一用来验证,三分之二用来训练,每次用不同的三分之一来验证,取这三种情况结果的平均值作为评价模型的标准,选出最好的模型,然后用最好的模型对全部的数据进行训练,这样就不会过拟合(overfitting)在测试集上。
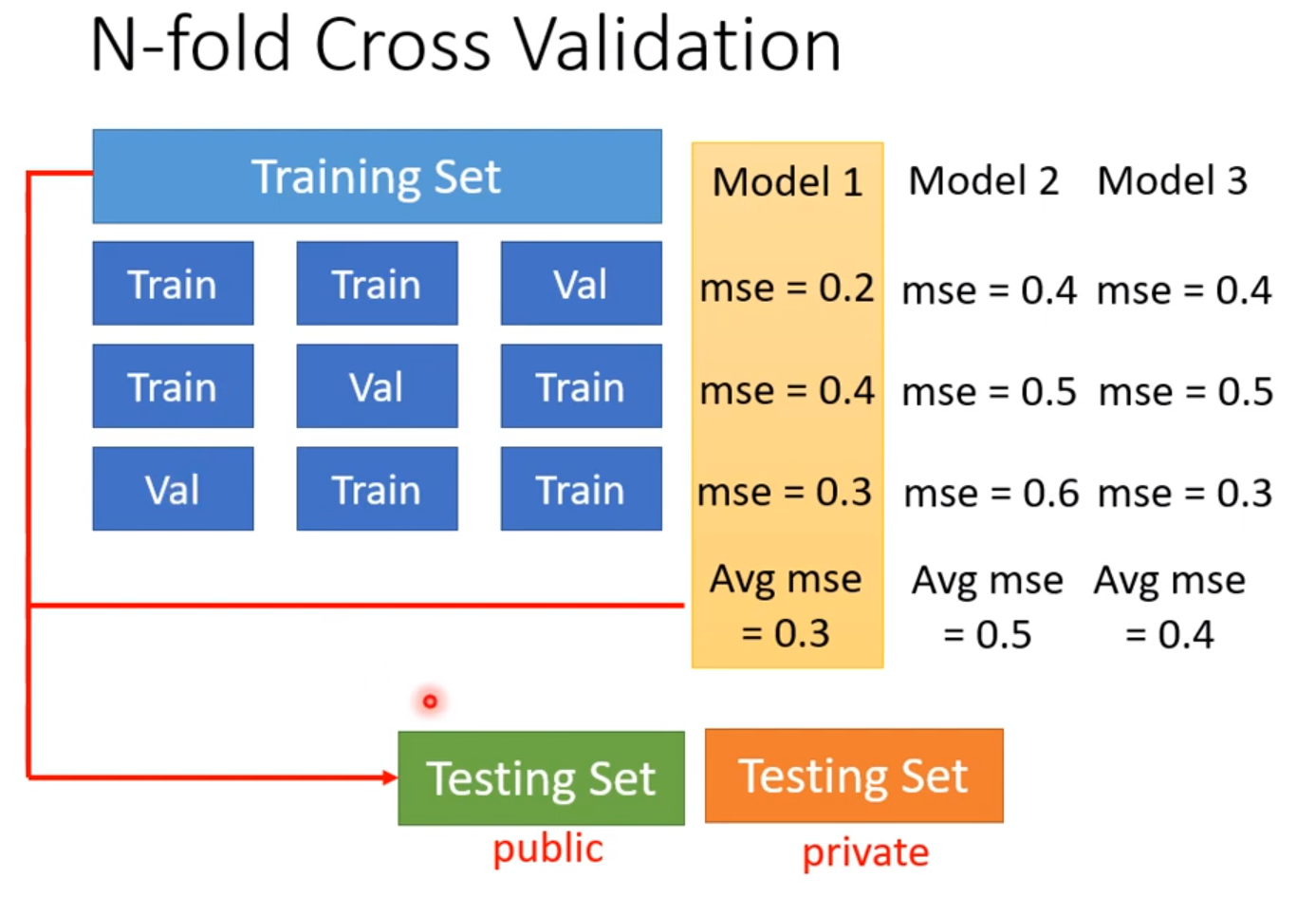
训练的模型还有一种情况使其在测试集上表现糟糕:那就是Mismatch,测试集和训练集的分布不同,也就是出现了反常的情况,以往的经验已经不能作为判断的标准,就算增加再多的训练资料也无济于事。
类神经网络训练不起来怎么办
局部最小值和鞍点
当一个神经网络的Loss不再下降时,可能是卡在了局部最小点(local minima),也可能卡在鞍点(saddle point),也有可能是局部最大点(local maxima)。这些点统称Critical Point。 在Critical Point时有导数为0但二阶导不为0, 有:

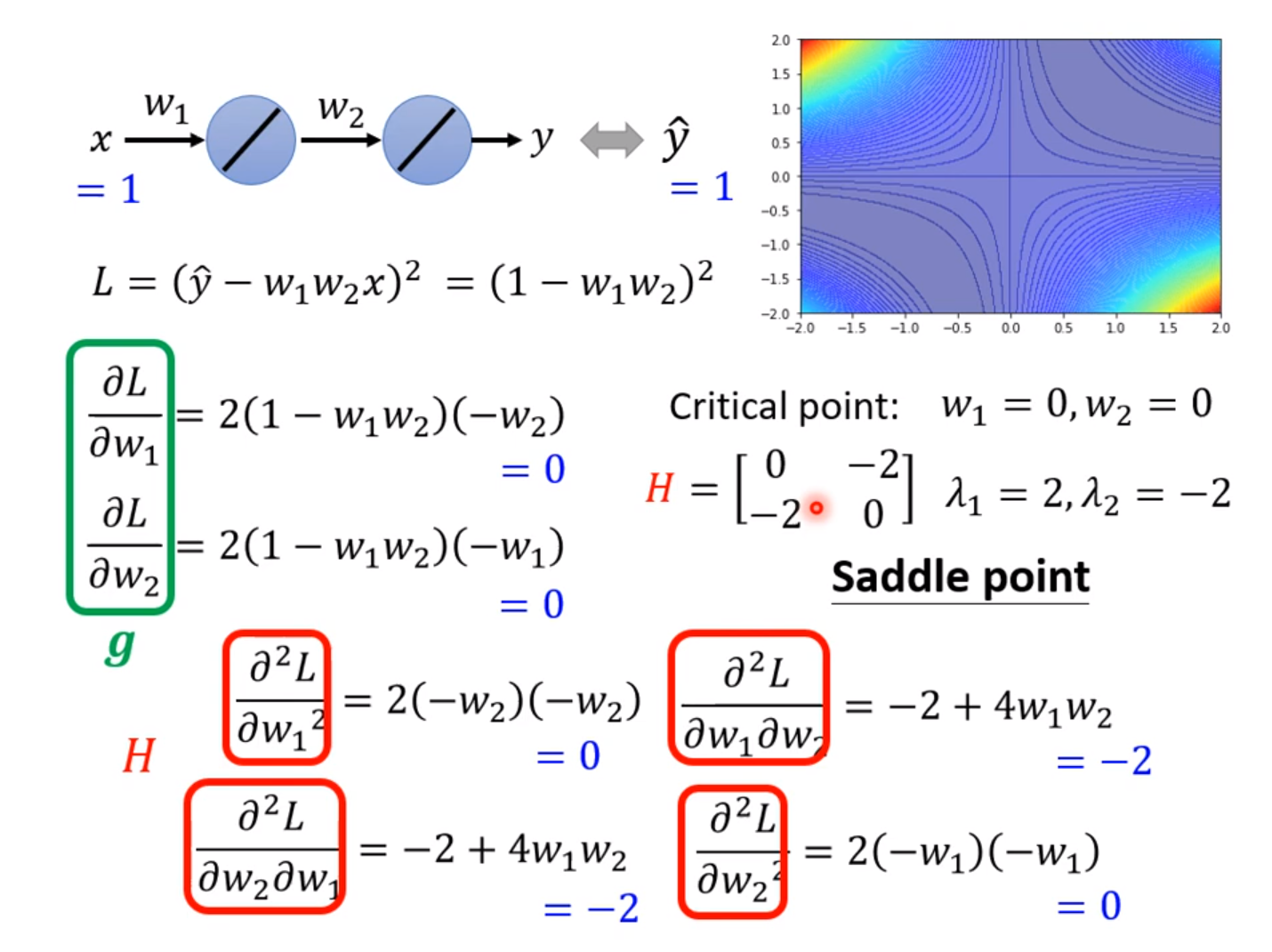
我们可以通过公式中二阶导的项的正负来判断具体是什么点,如果对于在CriticalPoint附近的任意θ,都使得这个二阶项大于0,即H是正定矩阵,该点一定是Local Minima。如果H是负定矩阵,那么该点一定是LocalMaxima。如果H非正定也非负定,那么该点是一个SaddlePoint。判定正定负定的标准只需看矩阵的特征值(eigen values)是全正还是全负即可。而这个矩阵叫做Hessian矩阵。H矩阵不仅指出了该点所处的状态,还指出了参数更新的方向。

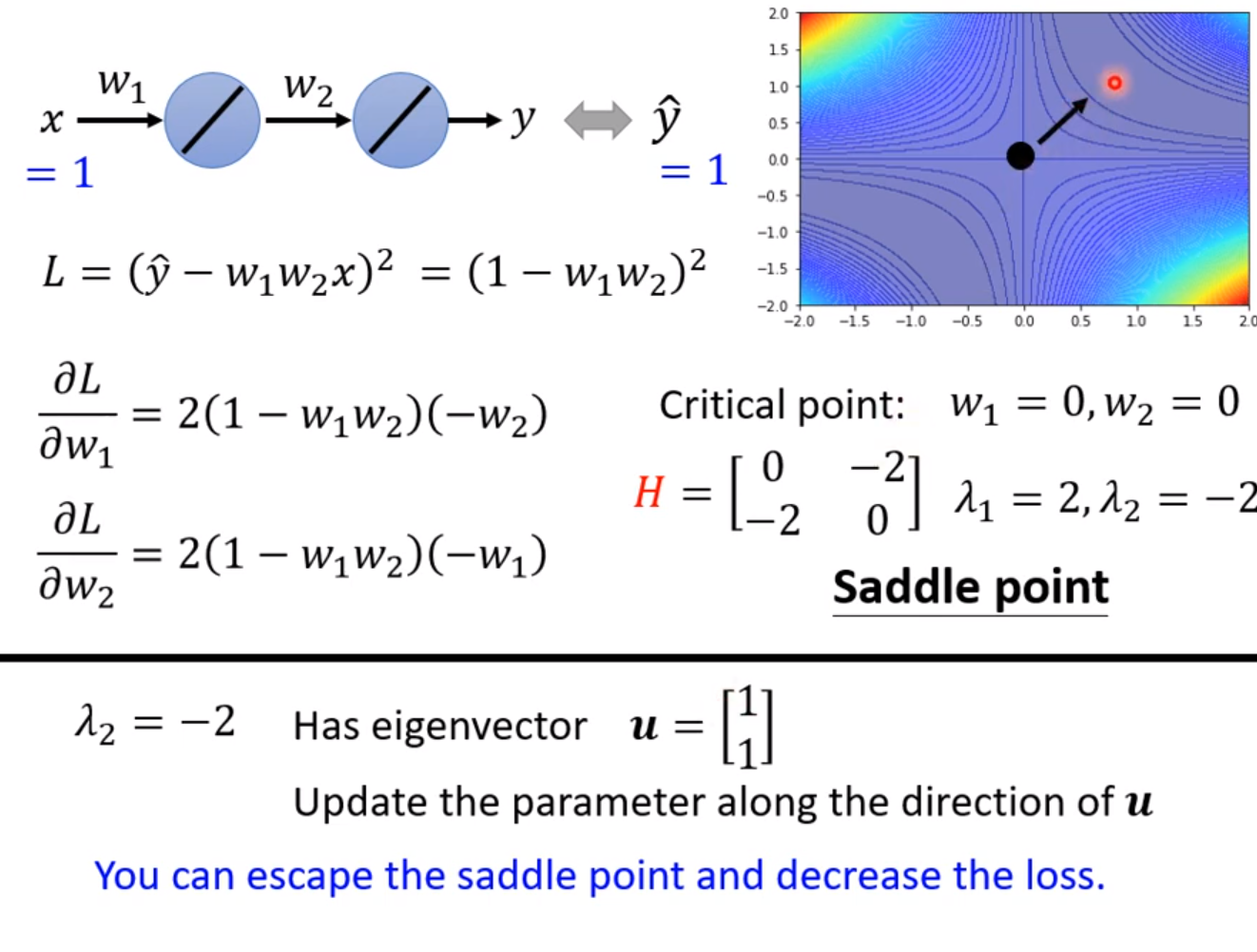
结论:在处于鞍点时,只需要参数往负特征值对应的特征向量方向更新,就能找到更小的Loss。这就是当梯度为0的时候参数的更新方法。但通常我们在计算时不会采用这个方法,因为运算量过大。
在一个神经网络模型中,参数动即上百万上千万,我们在平面上遇到的局部最小点往往是高维中的鞍点,维度越高,就有越多的路可以走,因此对于一个参数较多的神经网络,阻碍训练进程的往往是鞍点,而不是局部最小点。
batch
结论:batch_size较大时,训练速度较快,但是训练结果较差,这是optimization的问题。batch_size较小时,训练速度较慢,但训练结果较好。原因是大batch_size容易卡在鞍点出不来,而小的batch_size因为每个batch的差异性,往往另一个batch就能越过原来batch的鞍点使得训练继续下去。而且采用大的batch_size时容易在测试集上表现较差,这就是overfitting。
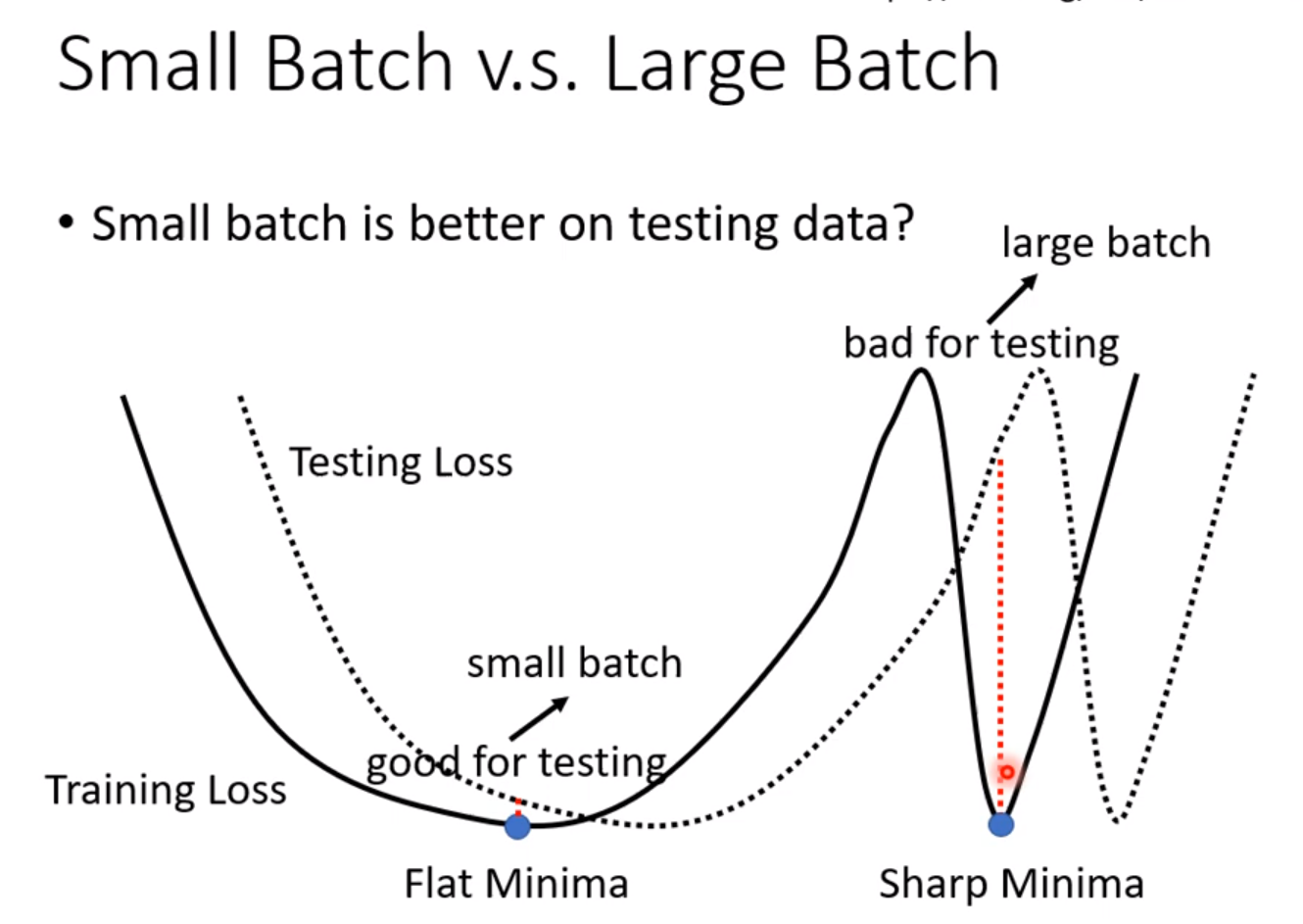
其中有一篇paper的解释是小的batch_size容易跳出较为狭窄的localMnima而倾向于宽阔的localMinima,而大的batch_size容易陷入狭窄的localMinima,而train出来的function和test或者实际的function是有差距的,而狭窄地带周围梯度较大,一点差距就会导致Loss迅速变大,泛化性变差。这就是为什么小的batch_size训练结果较好的原因。
momentum
参考《深度学习中的优化算法串讲》。
自动调整学习率
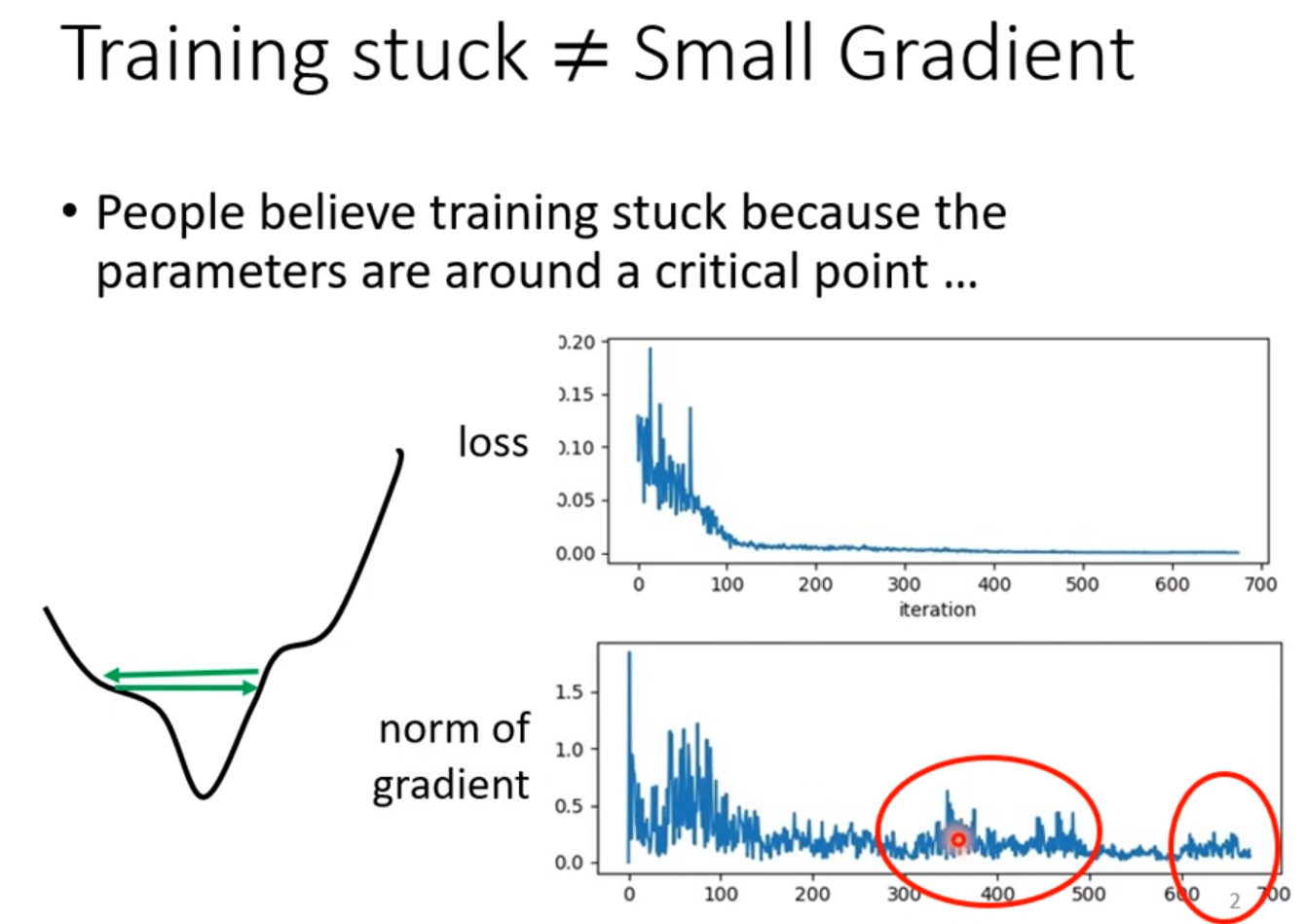
在训练的后期往往会在localMinima的附近来回震动,导致Loss没有办法继续下降,这时就要改进我们的优化算法了。
如果在某一个方向上的梯度较大,那么我们的学习率调小一些也不会妨碍我们的学习进程,如果在某一个方向上的梯度较小,那么训练就难以展开,我们需要大一些的学习率来维持训练进度。
更新学习率有几种方法:
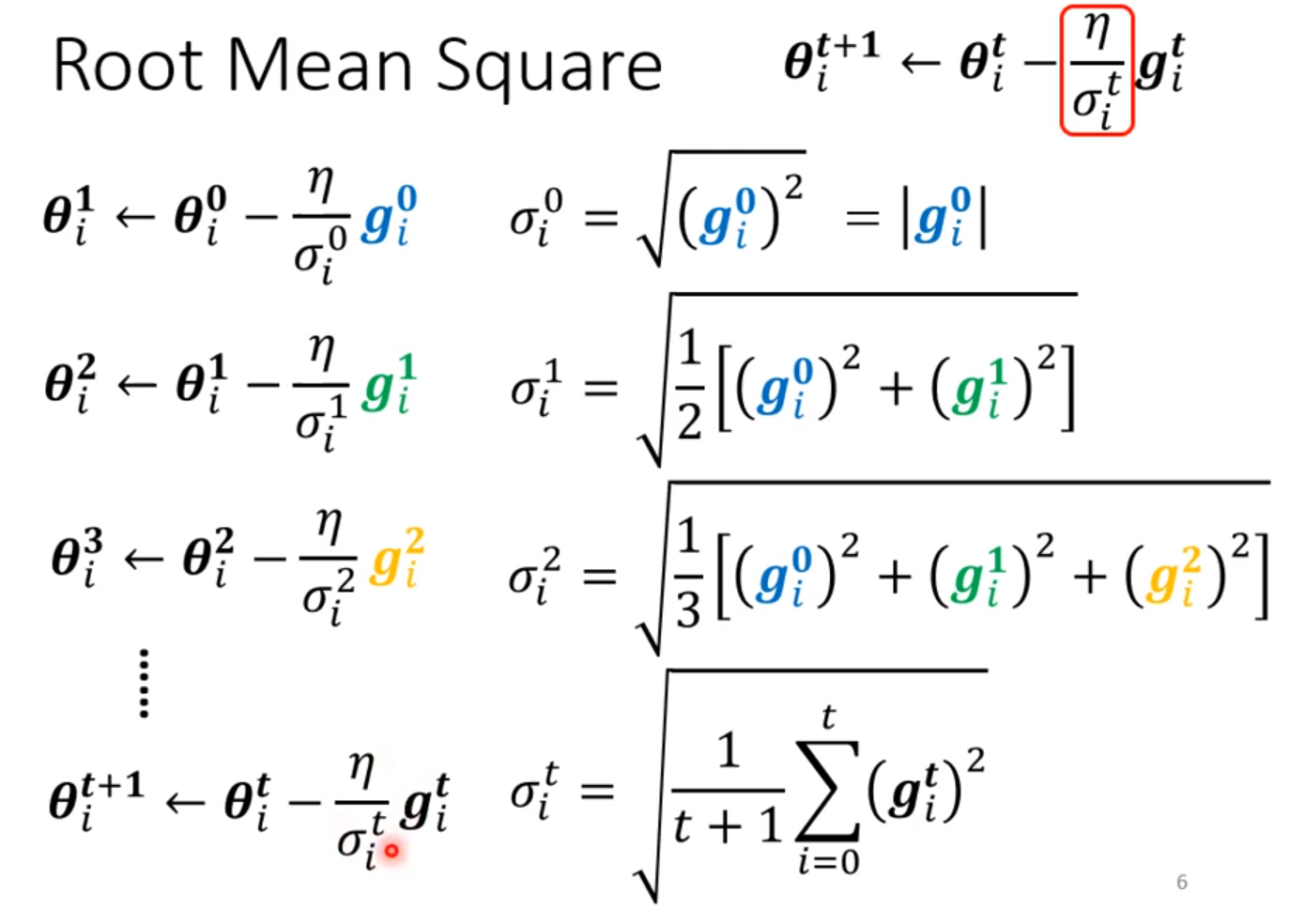
一种是初始学习率除以一个以往梯度平方的平均值再开根号,可以满足上述要求。这就是Adagrad的方法。缺点是更新速度较慢,以及在过于平衡的地方呆太久时会出现学习率的暴增,冲出原来的点一段距离,然后再慢慢回到原点,往往隔一段时间就会出现一次学习率暴增的现象。
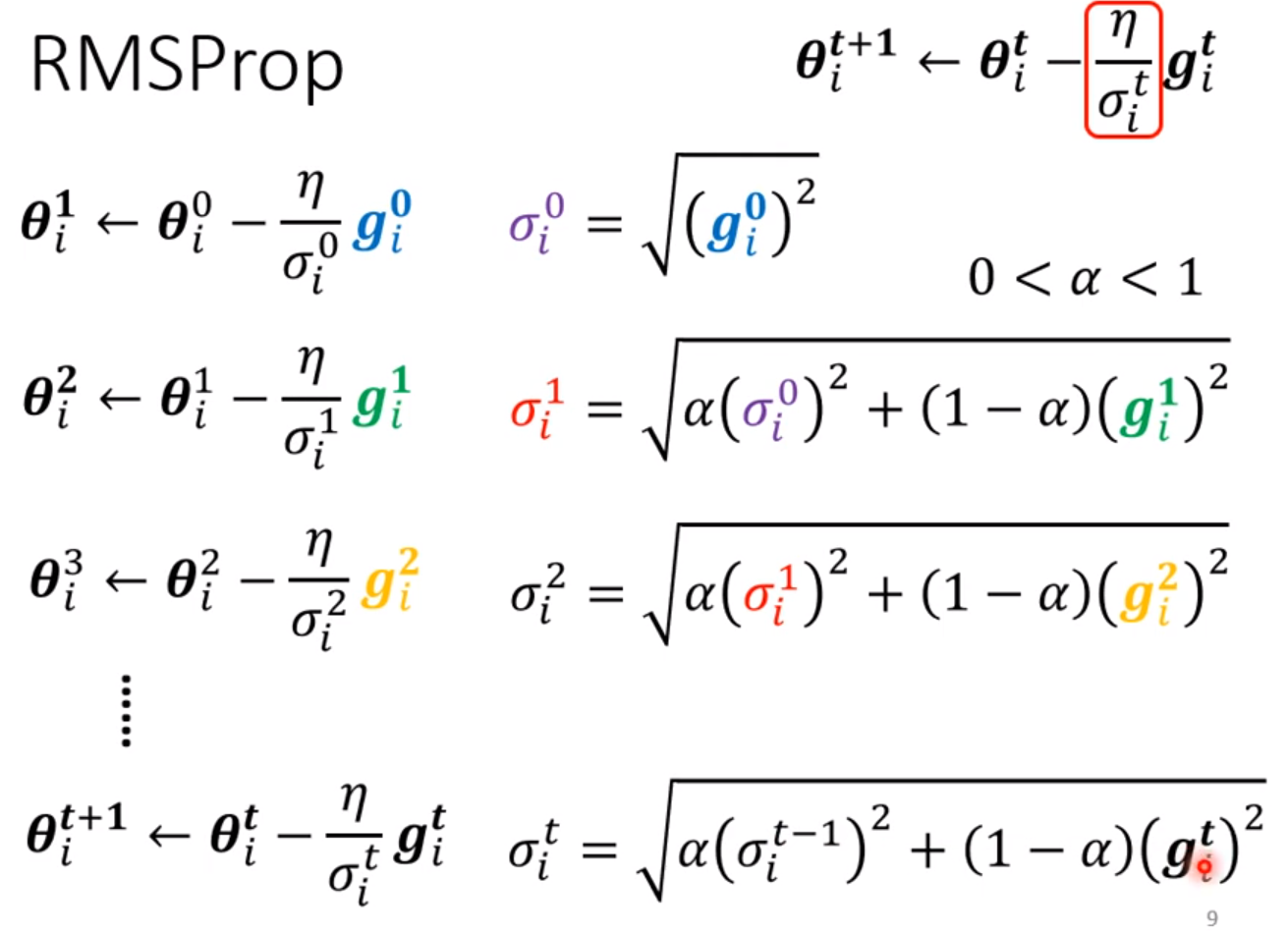
第二个方法是RMSProp,用了指数加权移动平均的概念。我们可以调整α这一项来决定之前的梯度占用的比例。这个方法的学习率变化速度要比Adarad快得多,特别是训练后期。但还是会出现学习率暴增的现象。

第三个方法是Adam,这个是最流行的算法,是Momentum和RMSProp的合体,性能比上面的都好得多。
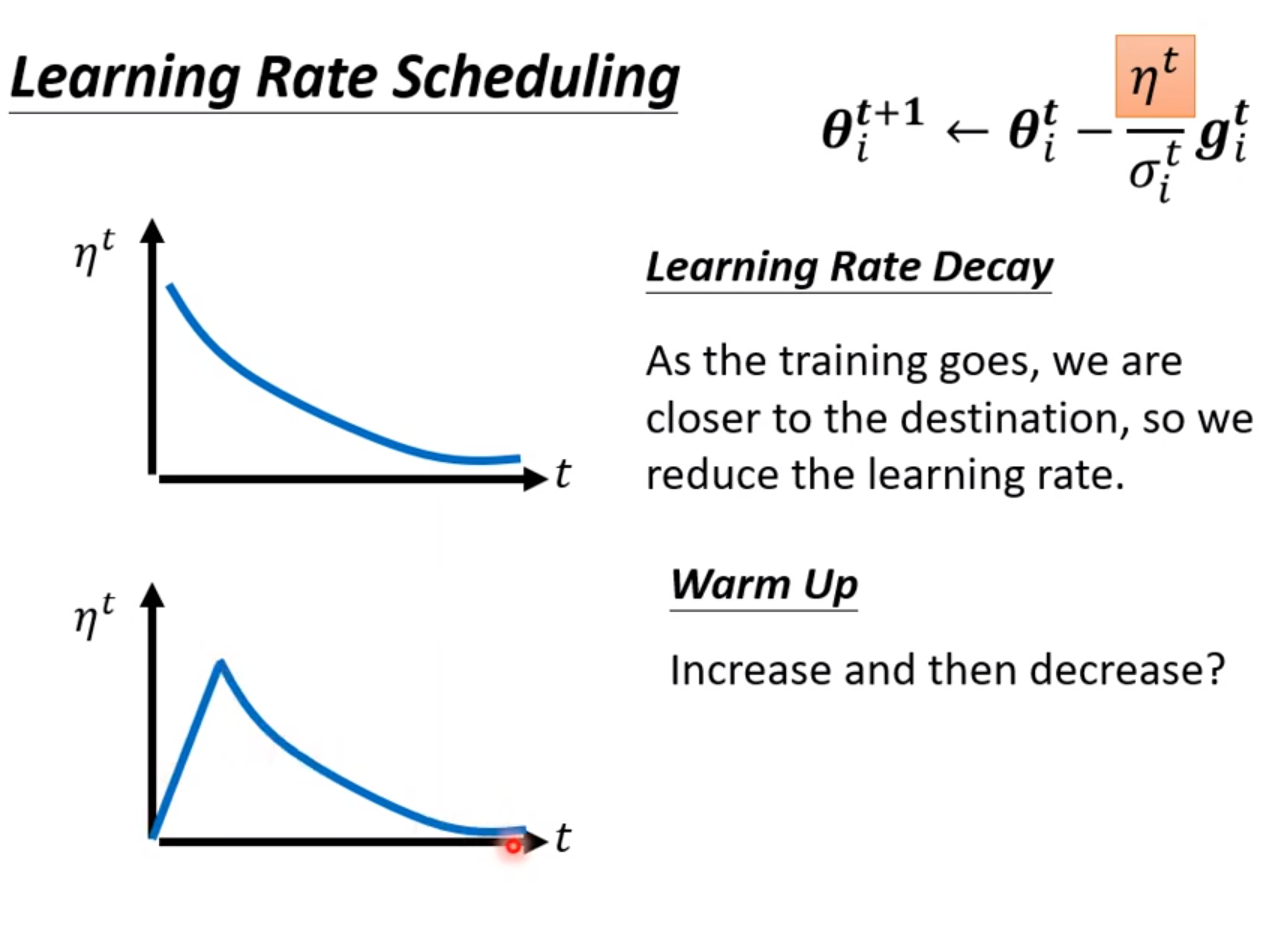
解决学习率暴增现象的一个方法是上面的初始学习率也可以动态调整,随着训练的进行慢慢调小(Learning Rate Dacay),可以解决这个问题。还一个方法叫做WarmUp,主张学习率先变大后变小。这是一个黑科技,很多论文都用这个方法,但不解释原因,但用了就是好。一个解释是开始的时候先让数据不要离原点太远,先进行一些探索,然后再决定方向。详细可以查看一篇RAdam的论文,有更多解释。

这个RAdam就是现在我们要用的优化算法的最终版本。

两种Loss函数的 比较
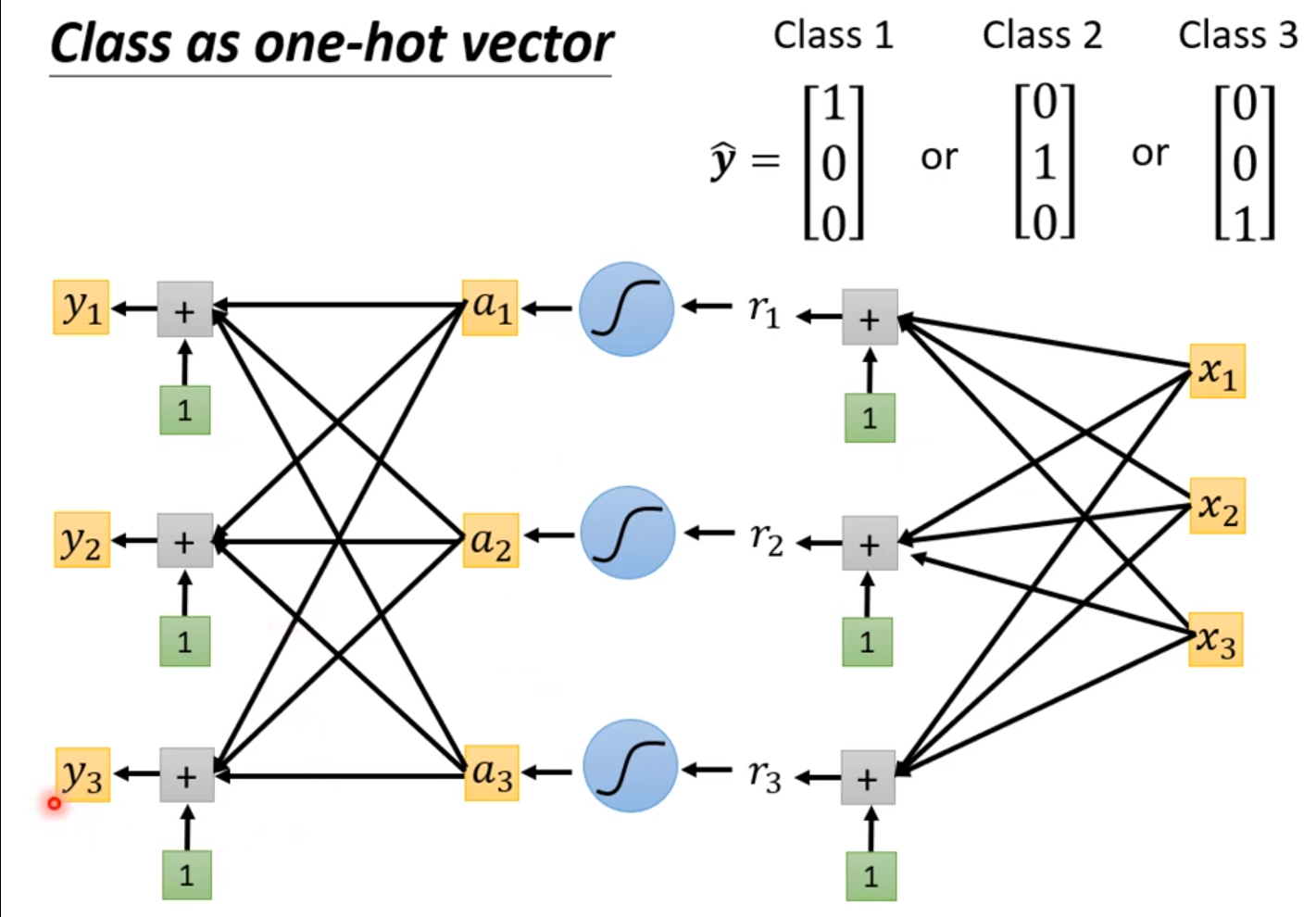
做分类需要用到的是one-hot向量而不是简单地用数字表示,我们期待输入对应的输出跟one-hot向量一致。

这部分的内容可以参考《pytoch教学及示例》的logisitic回归的内容。softmax的作用是可以让y映射到0和1直接并且所有的输出节点的值加起来等于1。
这个时候有两个计算Loss的方法,一个是Mean Square Error(MSE),一个是交叉熵Cross Entropy,和最大化可能性等价(maximizing likelihood)
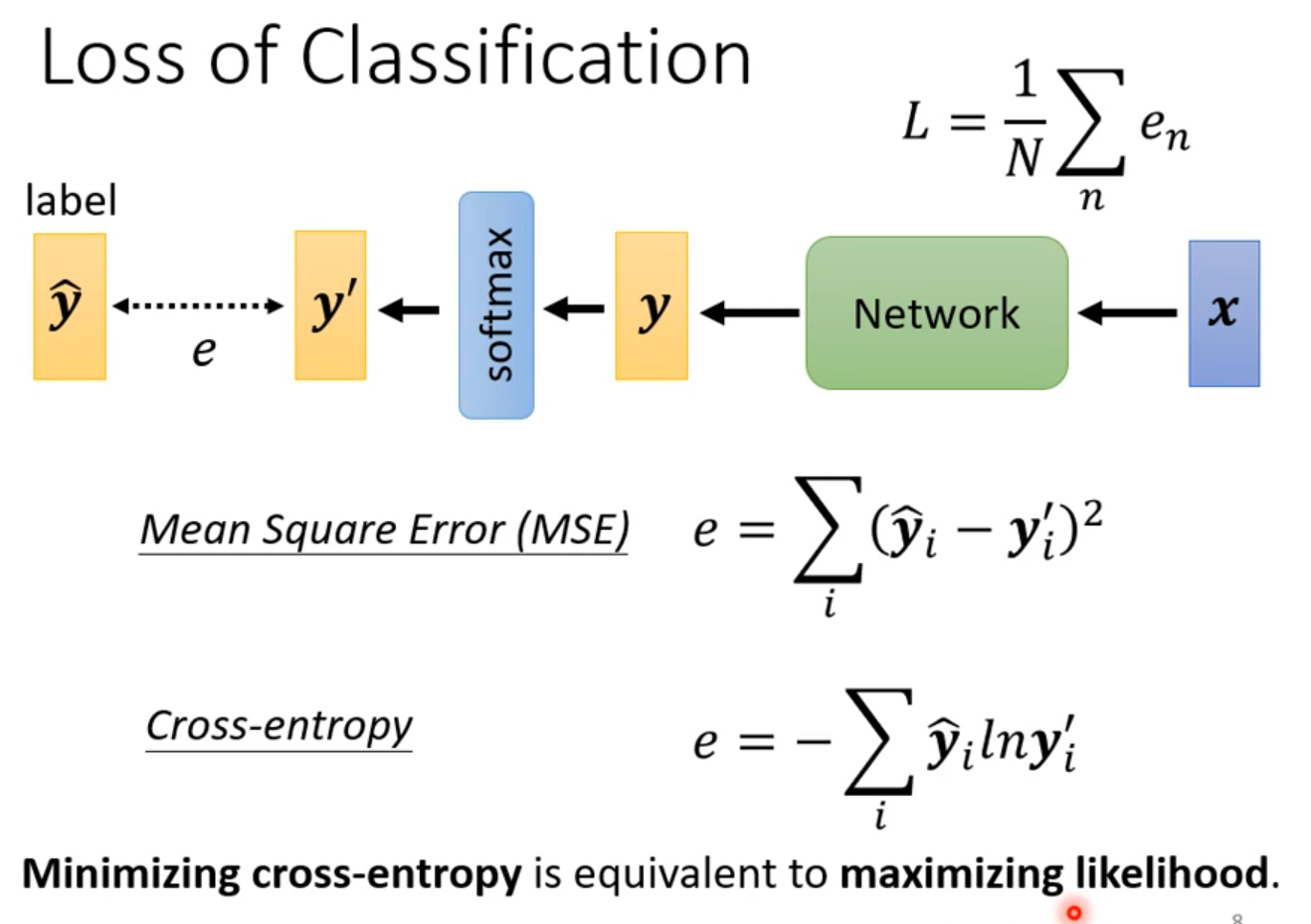
这两个方法比较,交叉熵损失更为优秀,最常用在分类问题中,以至于softmax和Cross Entropy都被绑定成一个函数了。
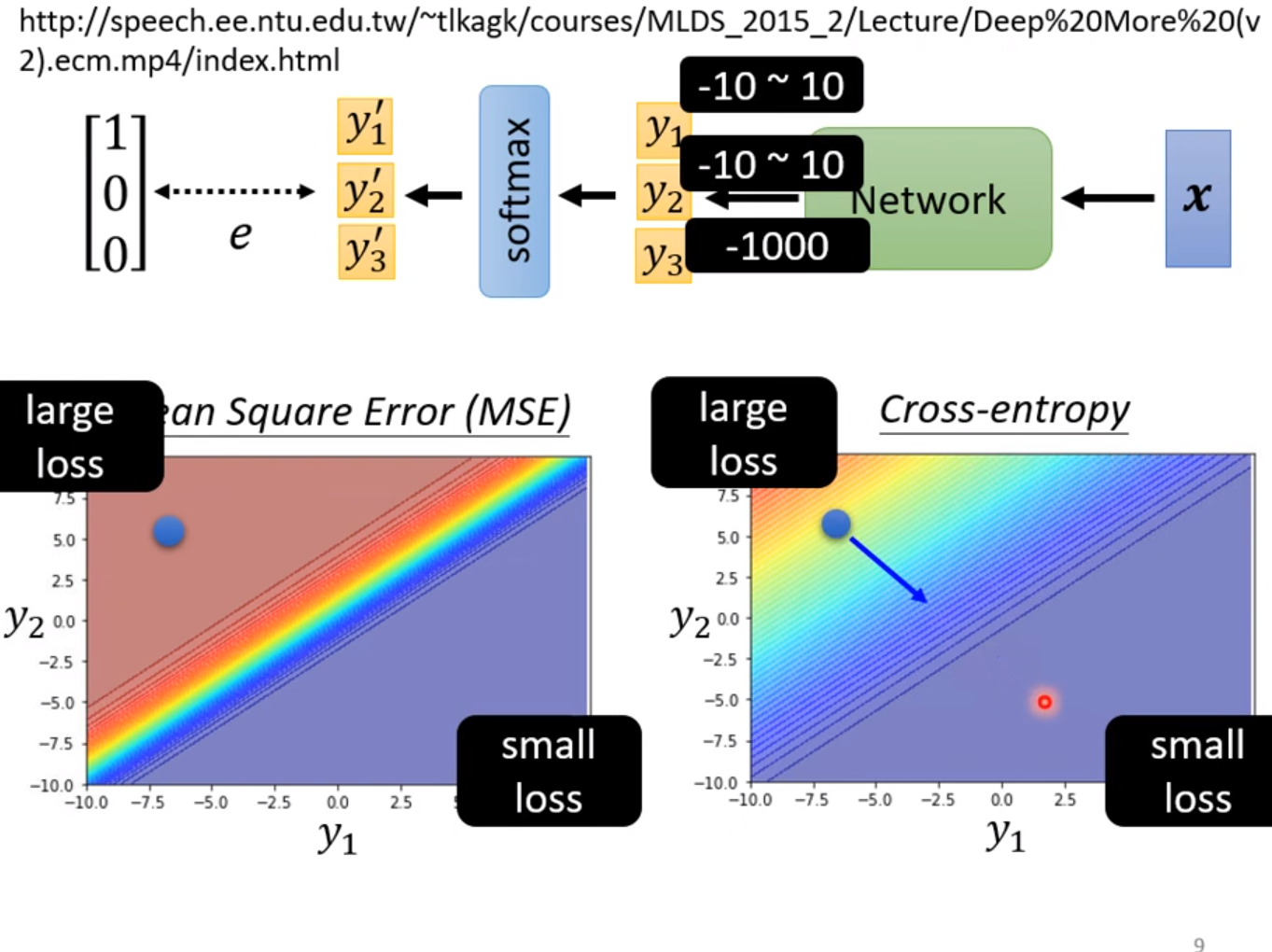
上图是比较当输出预测值y在两种方法相同的情况下,随着y的变化各种Loss的变化。在MSE中Loss较大和Loss较小的地方梯度都是很小的,即这就导致了如果初始点在左上角的话,训练的进展会非常缓慢,甚至会训练失败;而交叉熵损失即使在Loss较大的地方梯度都都仍然有明显的梯度变化,更利于训练。
批次标准化(Batch Normalization)
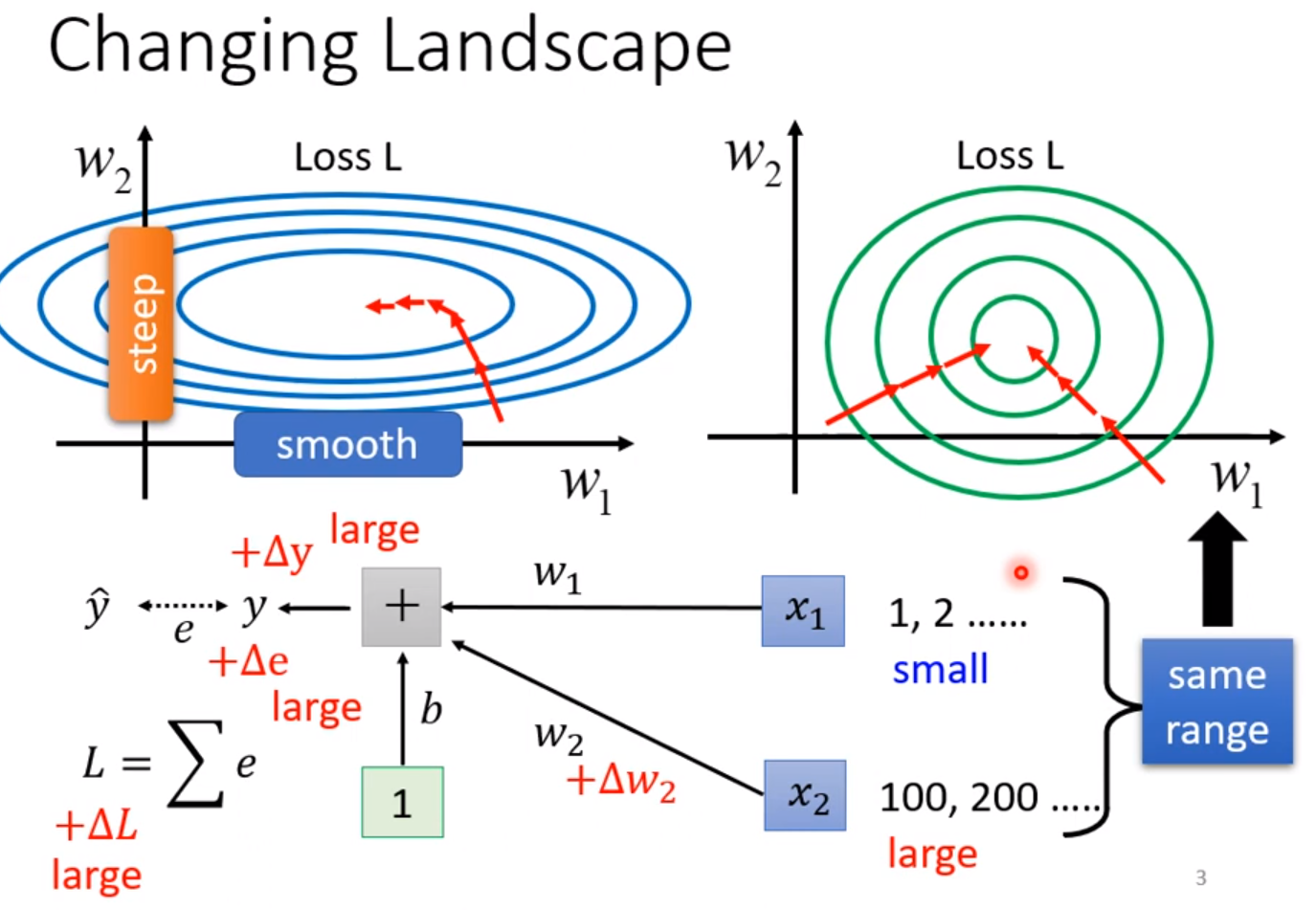
通常梯度的变化跟输入的数据息息相关,即使w变化相同的范围,x的数值大小不同也决定y的变化不同,往往x较大的时候,对应的权重w变化一点点就会造成y巨大的变化,因此x的大小就是造成不同的w梯度变化不一的原因,而如果梯度都是这样大小不一的状态,我们一般的优化算法就很难得到好的结果。如果我们能限制x的范围,使得不同x尽量在一个数量级上,那么梯度的差距就不会这么明显,训练起来就更加容易。这些方法通常为Feature Normalization。
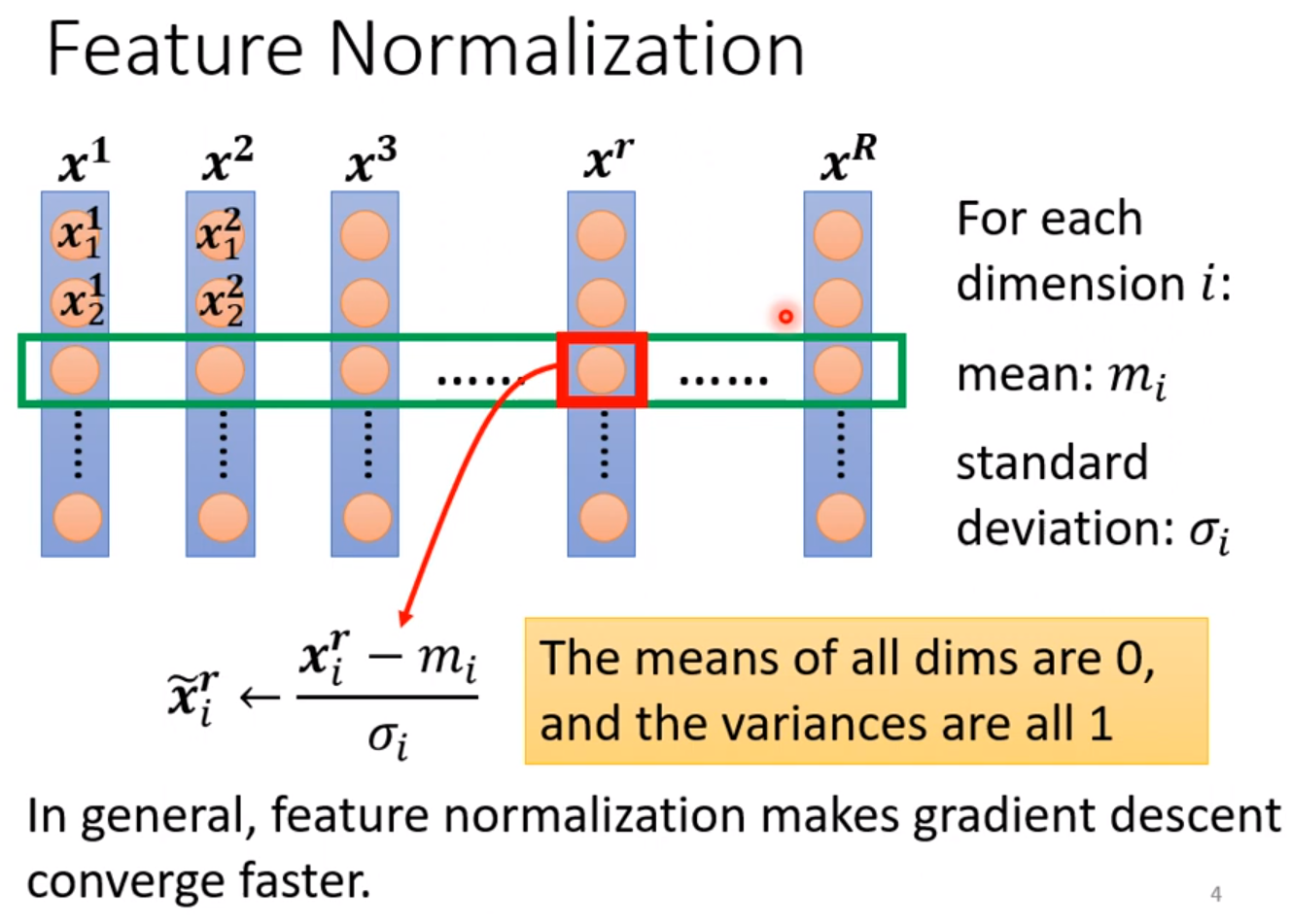
步骤是计算输入x每一个维度的平均值和标准差,通过公式映射到(0,1)分布:
$$
\hat{x_i^r} = \frac{x_i^r - m_i}{\sigma_i}
$$
对每一个维度i都进行这样的变化,可以使训练更加顺利。在我的文章《pytorch教学及示例》中,对全部的x使用了这个映射。
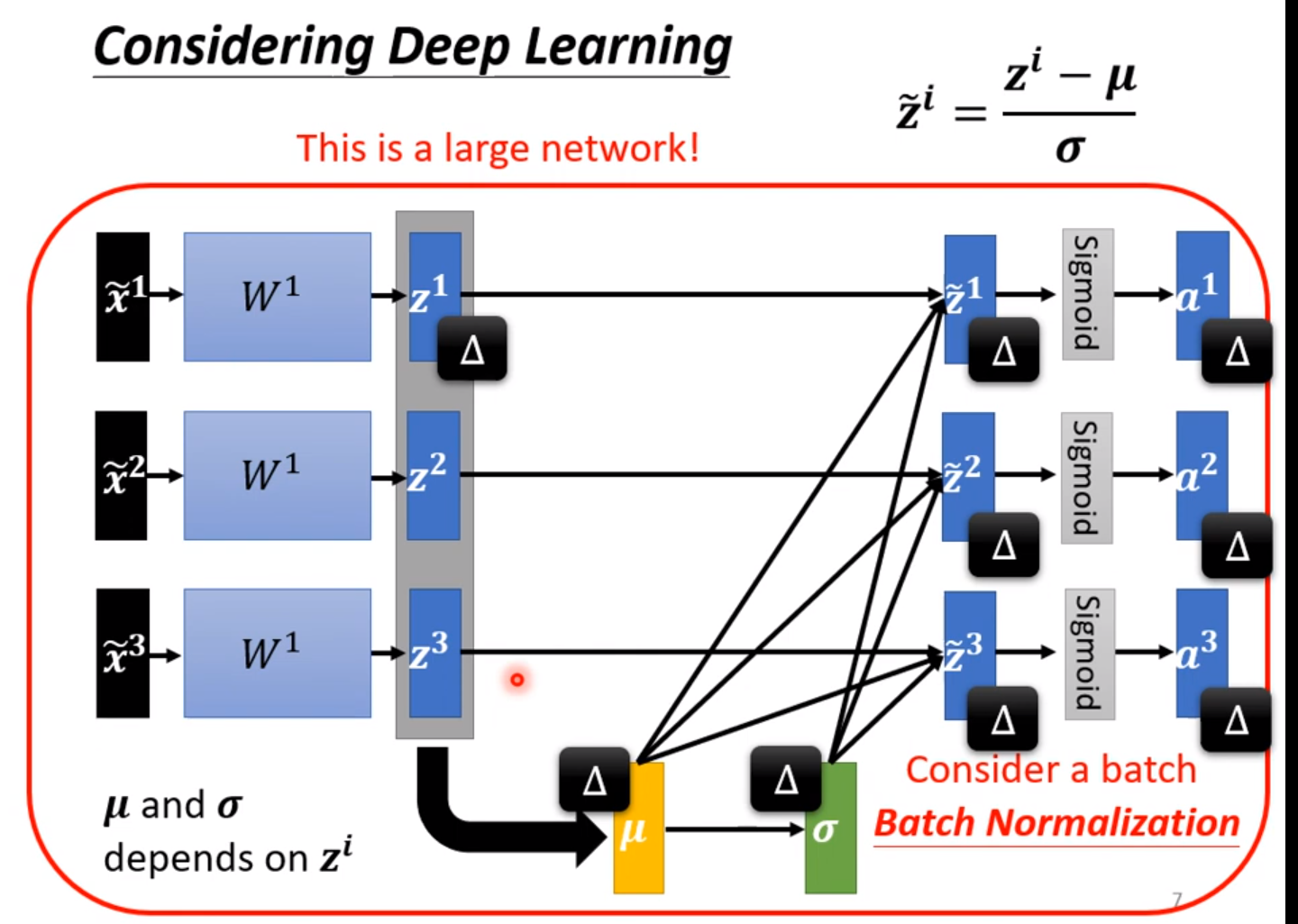
同理我们不仅可以对原来的x进行映射,我们也可以对x进行线性变化后的层进行映射,这样又有利于下一层的线性层进行训练,一般来说我们每次只用一个batch进行计算,这就是Batch Normalization。
如果不需要平均值是0,或许这样对训练会产生负面影响,我们可以再加入线性层进行调节。
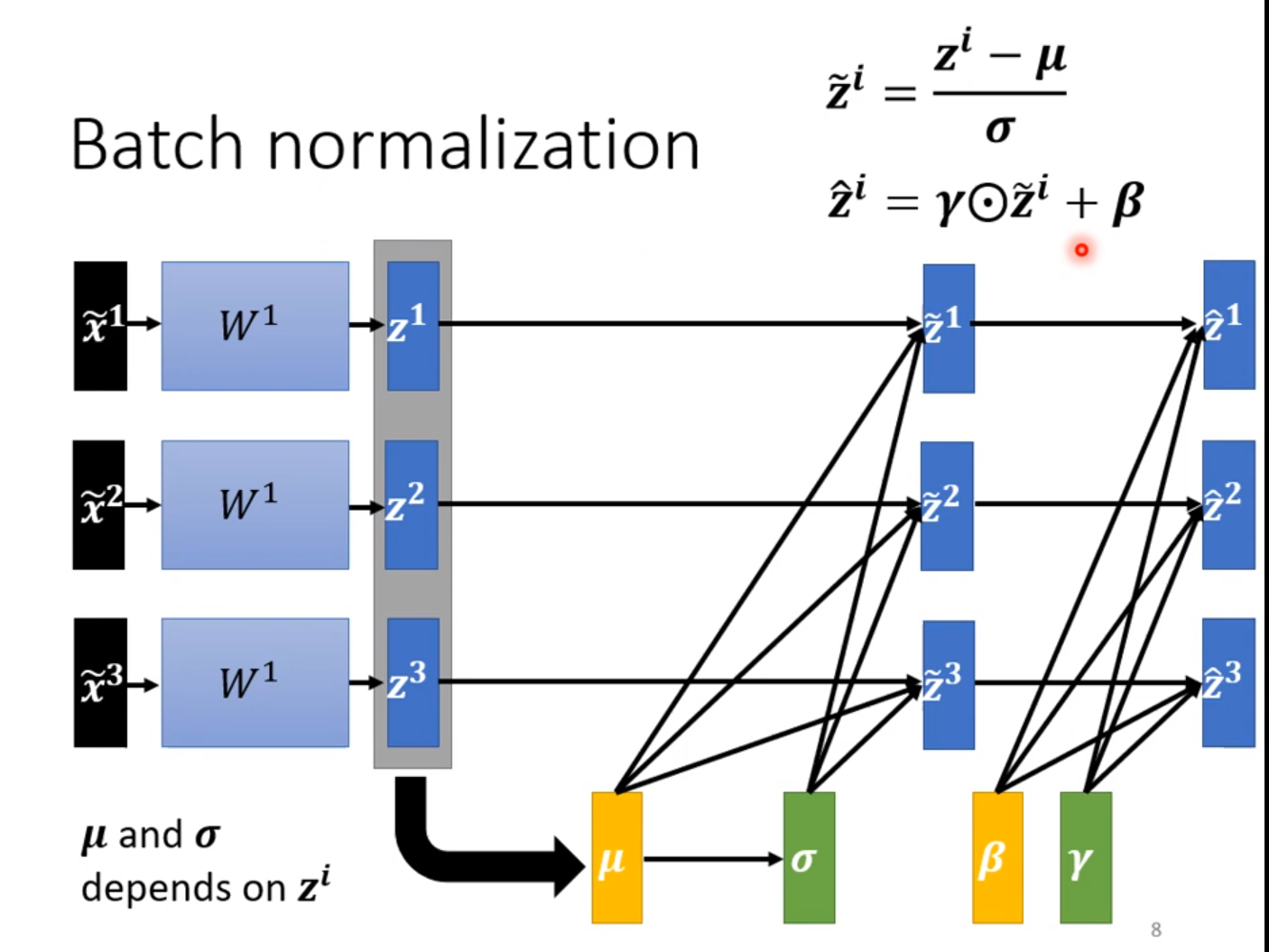
当程序真正上线应用的时候,我们需要对传进来的每一笔资料都做一次测试,我们无法等待凑足一个batch再进行测试,而不凑足一个batch是无法进行平均值和方程的计算的,也自然不能进行Batch Normalization。这是就需要用到往常的资料了:

这就是根据以往的平均值和方差计算指数加权移动平均值的方式,这样就可以对新进来的测试数据进行标准化变换。
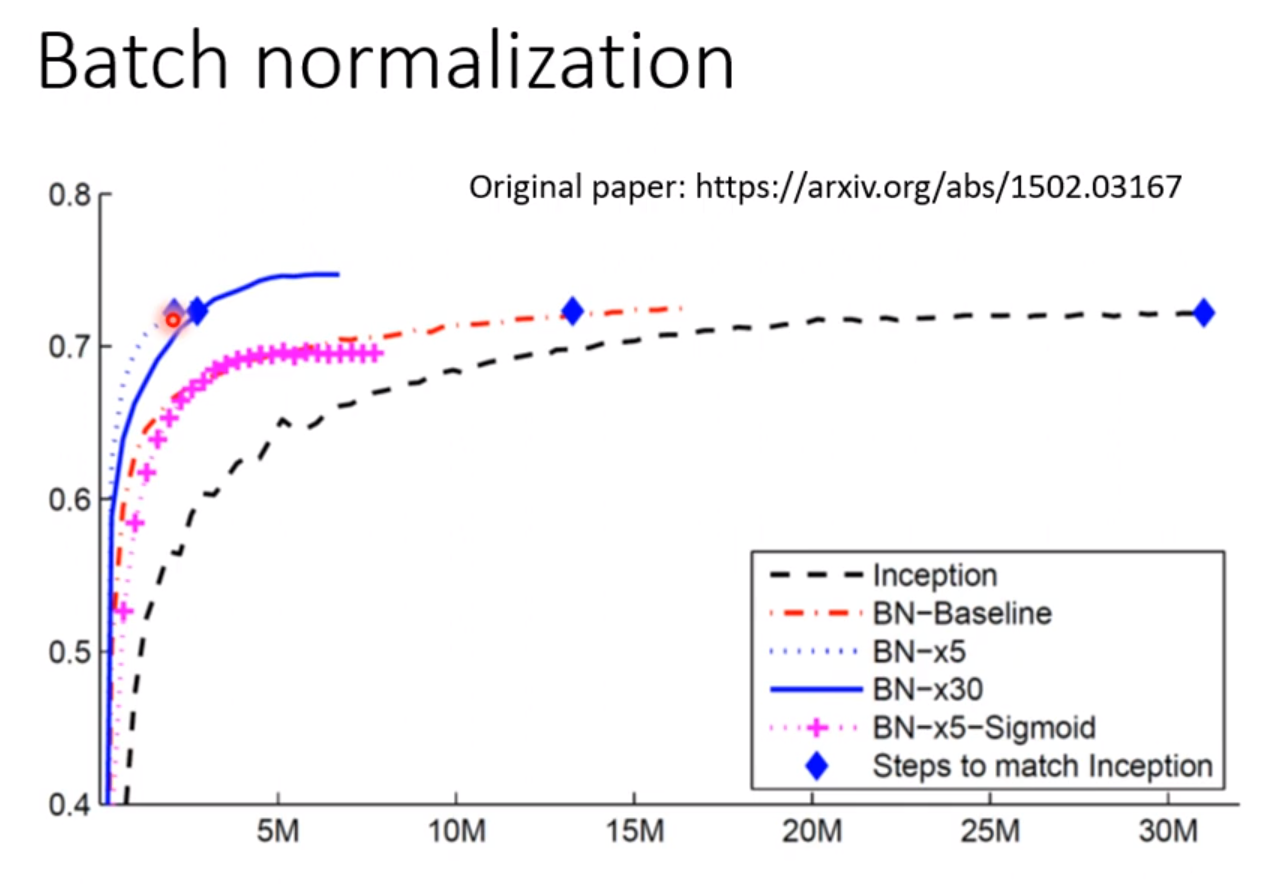
可以看到,进行标准化处理的数据的训练速度要比没有做标准化处理的数据的训练速度快得多。
Batch Normalization不是唯一的标准化方法,还有一些方法如图:

卷积神经网络(CNN)
这部分内容请参考《Pytorch教学及示例》,请和结合起来看,有非常详细的讲解。
如果对一张图像三个通道的每个像素都使用DNN进行链接,那么模型的弹性太大,很容易过拟合Overfitting。而对一张图片来说分类重要的是识别出图片中的某一个特征,而不局限于一个像素点,很多时候我们不需要看整张图片,只需要看图片的某一部分就可以很肯定地做出分类。因此模型弹性太大反而因为选择过多而坏事,根据样本的特点选择适合的模型可以使得模型的泛化性更强。
因此我们需要卷积核(kernel)对特征进行提取,一般的卷积核大小都是3*3的。也可以是其他n*n的(n为奇数)。
在同一个通道内的所有区域都共享一个卷积核,因此当不同区域出现相似的特征时,它们的输出也将会是相似的,它们共用的这组参数叫做fiter。当三个卷积核分别扫描了三个通道过后,产生的值相加,这时就产生了一个Feature Map。这样的操作可以进行很多次,每一次都产生一个新的通道,具体计算之后产生多少个通道是我们自己决定了,n个通道就对应n个特征的提取,通道数越多,特征数提取的越多。有n个通道就有3*n个卷积核。上面就是一个卷积层的计算,模型中可以有很多个卷积层。这是因为一个图片特征的大小都是不固定的,如果在3*3的区域内无法找到有效的特征,这就需要做第二次的卷积,由于第二次卷积是基于第一次卷积的特征结果之上的,第一次卷积已经把九个像素的内容重叠成一个特征了,因此如果第二次卷积也是用3*3的卷积核,它的特征提取范围将要比原来大一些,卷积层叠的越深,特征提取的范围越大。
第二个特征提取的方式是池化层Pooling,其实质是把图片缩小。方法是把图片分成一个个n*n的像素单元,然后每个单元取最大值代替整个单元,这就是最大池化(Max Pooling)。这样就能把图片的宽和高同时缩小n倍,使得数据量变小,特征更明显,但如果特征太小,这样做特征会丢失。所以池化层的层数和大小要控制。好处是大大减小数据量和运算量,如果硬件允许,甚至可以不用做Pooling。
经过若干层的卷积层和池化层以后,我们再把数据展平放进全连接层中,最后通过softmax输出。这样就完成了分类。
应用:AlphaGo,机器下围棋,围棋盘就可以看成一张图片,黑子看成1,白子看成-1,没有子看成0,输入就是19*19的Tensor,输出就是下一步落子的位置。我们用CNN比DNN效果更好。但实际上AlphaGo没有用1或-1这种简单的方式来表示输入,在AlphaGo论文中,每一个位置都用了48个元素来表示此时的状态。第一个输入用的是5*5的卷积核,而为了不遗失信息,没有用Pooling。
然而CNN有一个缺点,那就是不能处理图片放大缩小后的分类,分类的物品必须在图片上的大小保持一致才行。因此在训练的时候,数据要进行Data Augmentation。就是把图片进行旋转,翻转,放大,缩小的操作,再放入训练集中。
拓展:有一个架构Special Transformer Layer,可以处理图片放大缩小等操作后的识别问题。https://youtu.be/SoCywZ1hZak
拓展:半监督学习
我们可以在将已知标签的数据训练好模型后,对为标签的数据进行预测,在预测的数据中挑选出比较可信的数据用预测的结果再加入训练中,这样有可能得到准确率更高的模型。
Special Transformer Layer
这也是神经网络中的一个层,接在CNN的前面负责对图像的缩放旋转的处理。
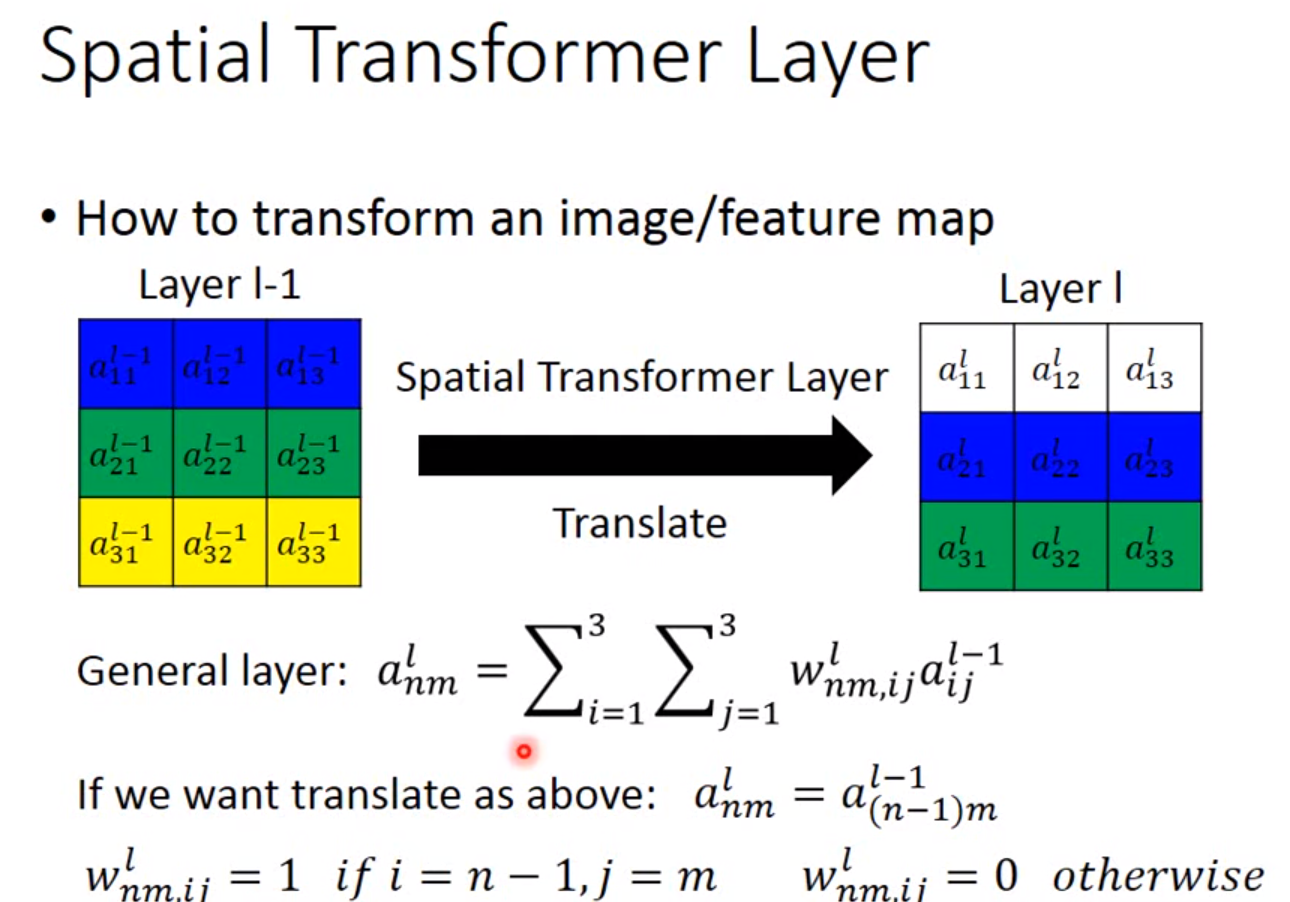
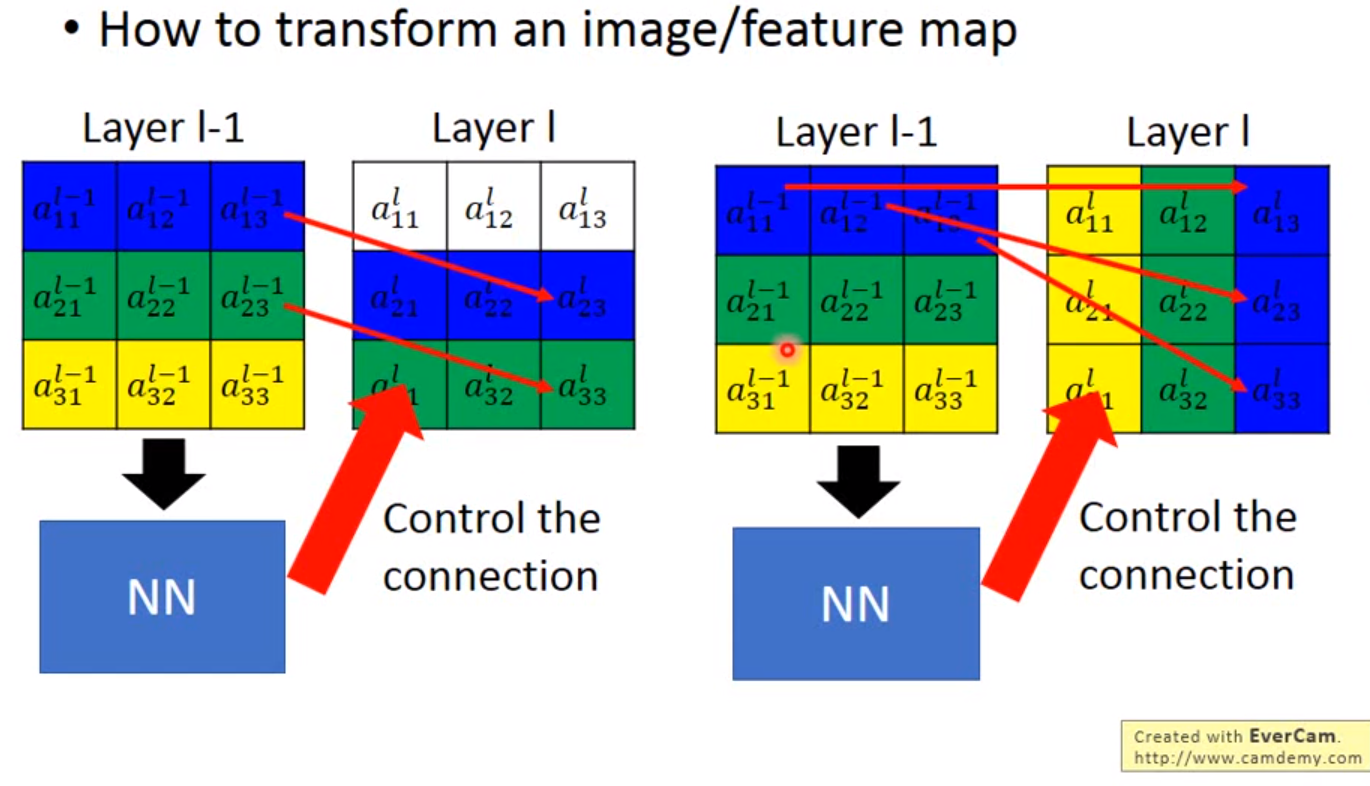
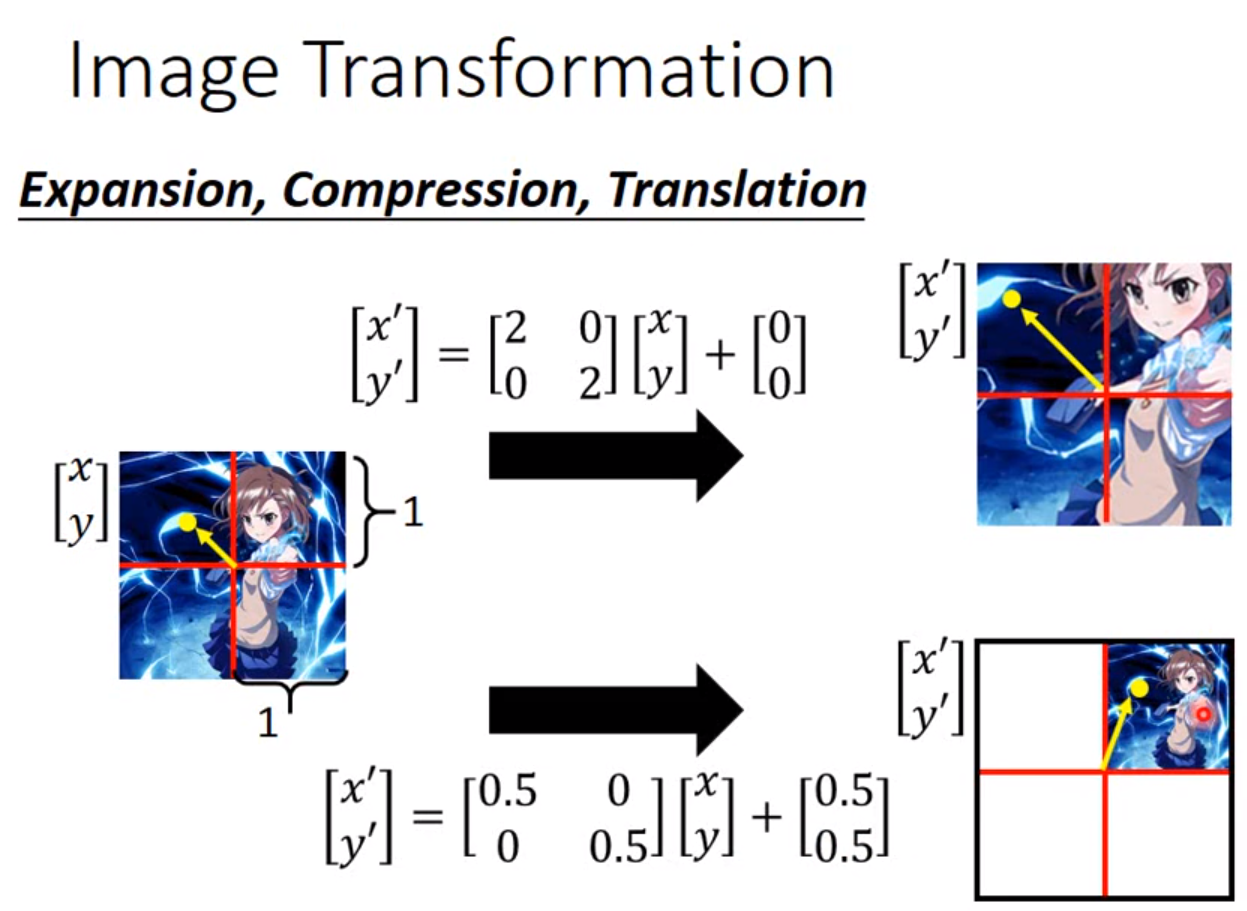
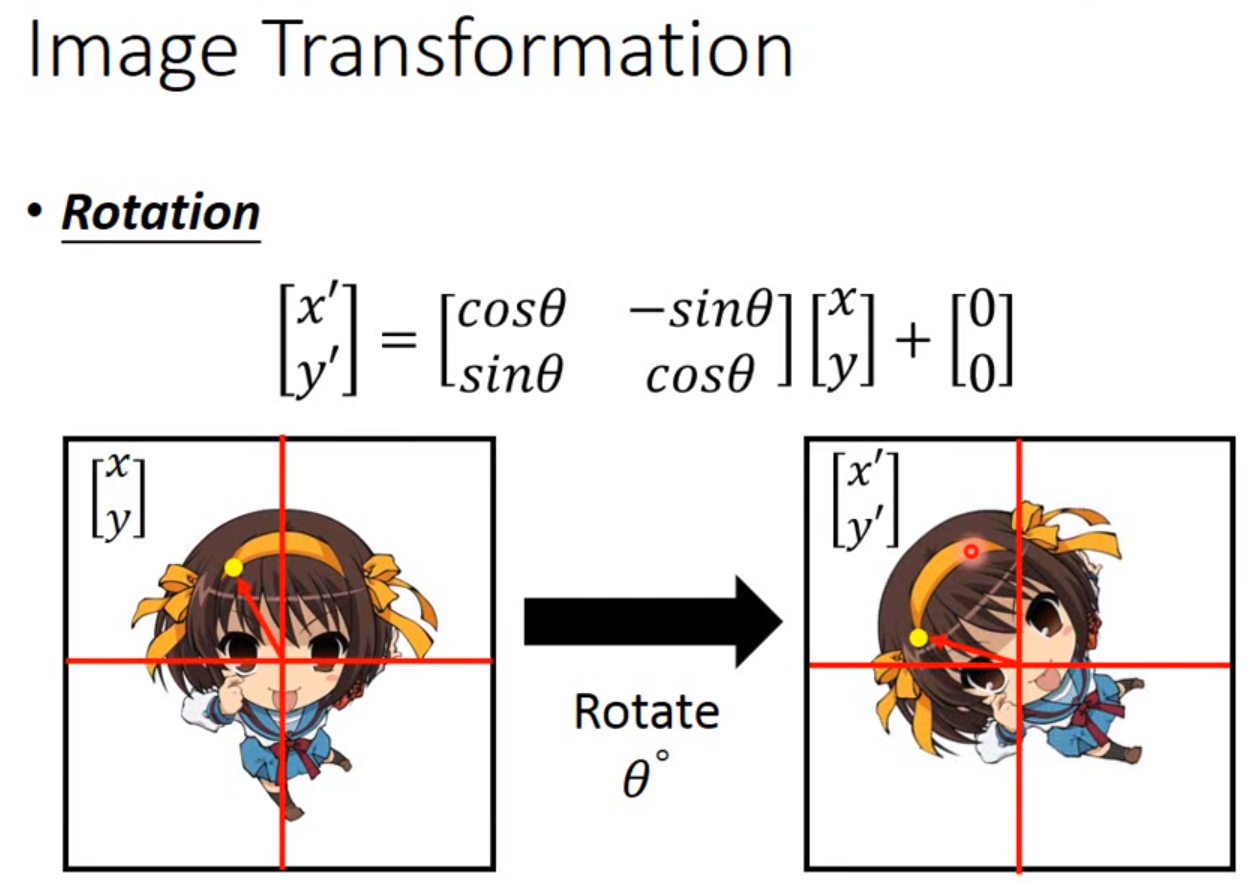
因此只要用一个2*2矩阵加上一个二维向量作为参数,输入一张图片的灰度的索引,输出的索引就可以让一张图片任意旋转缩放。

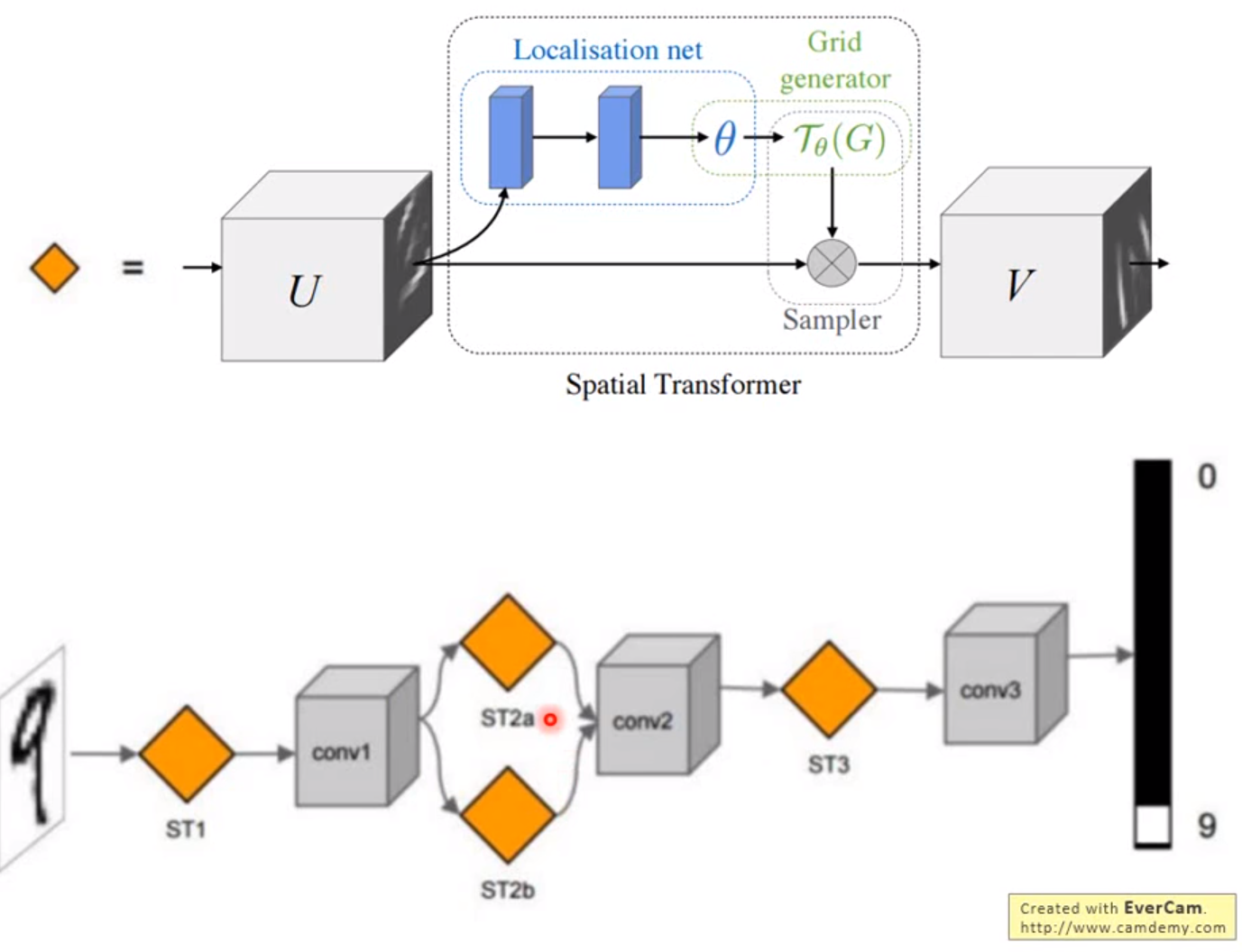
待完善。。。。
自注意力转移机制(Self attention)(未经验证)
https://www.bilibili.com/video/BV1Wv411h7kN?p=24&spm_id_from=pageDriver
这部分内容请参考《pytorch教学及示例》的RNN部分。很多事情Self attention可以取代RNN。从运算速度来说Self Attention会更有效率。
这部分内容往往用在自然语言处理中。如果每次输入的序列长度不一怎么处理?而且输出不仅考虑一个输入,还需要考虑一整个seqence的资讯。
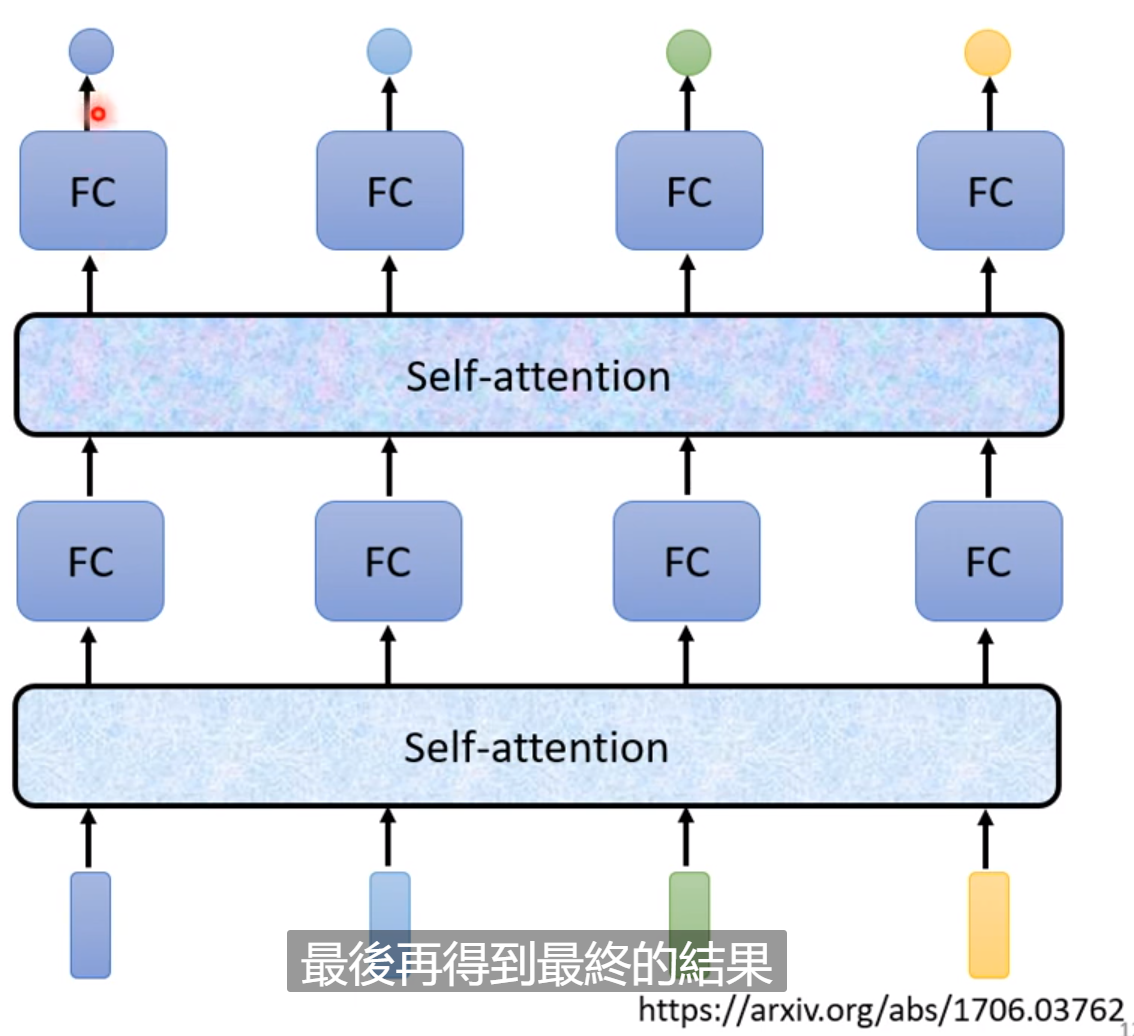
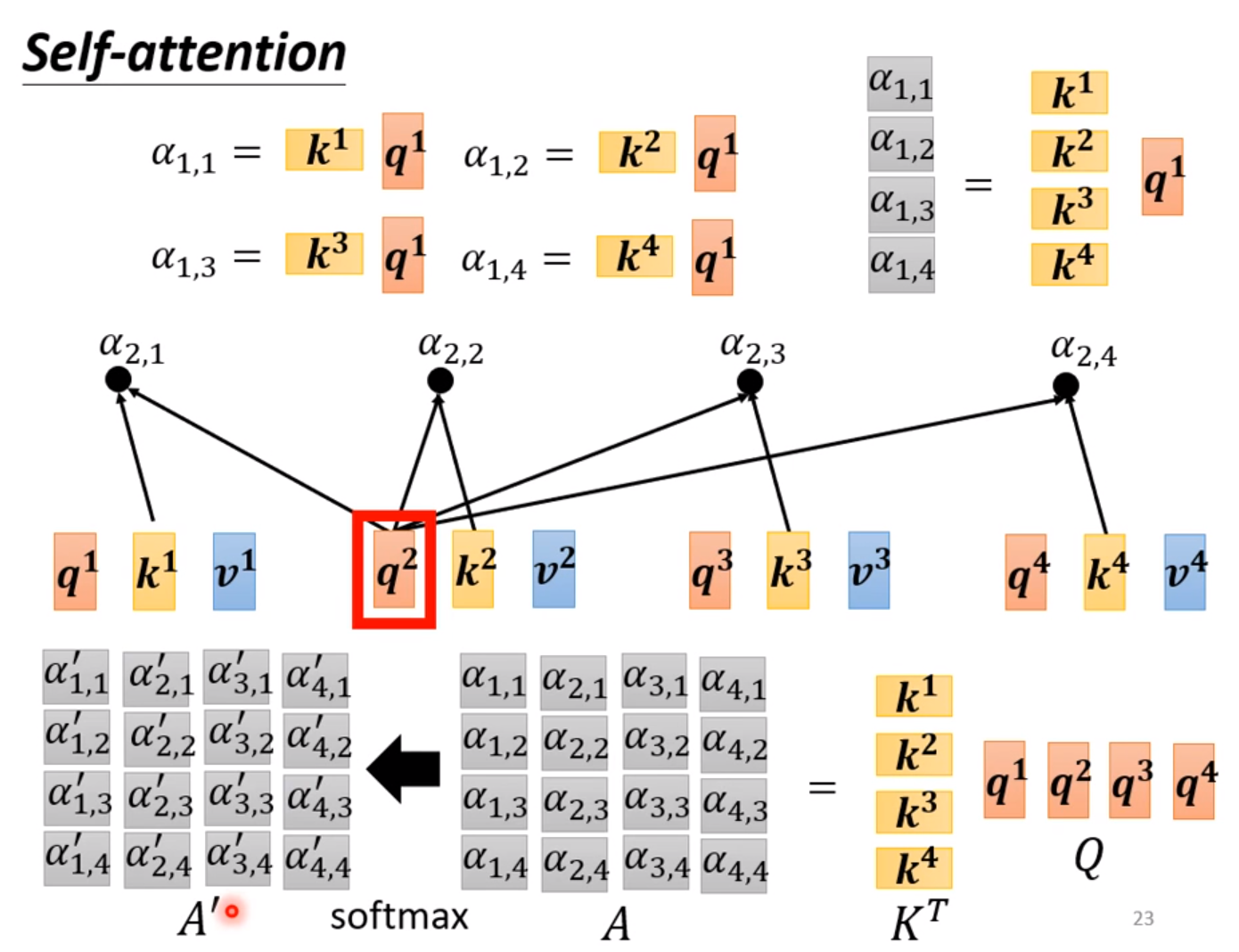
我们需要两两计算两个输入的相关程度,通过softmax输出。
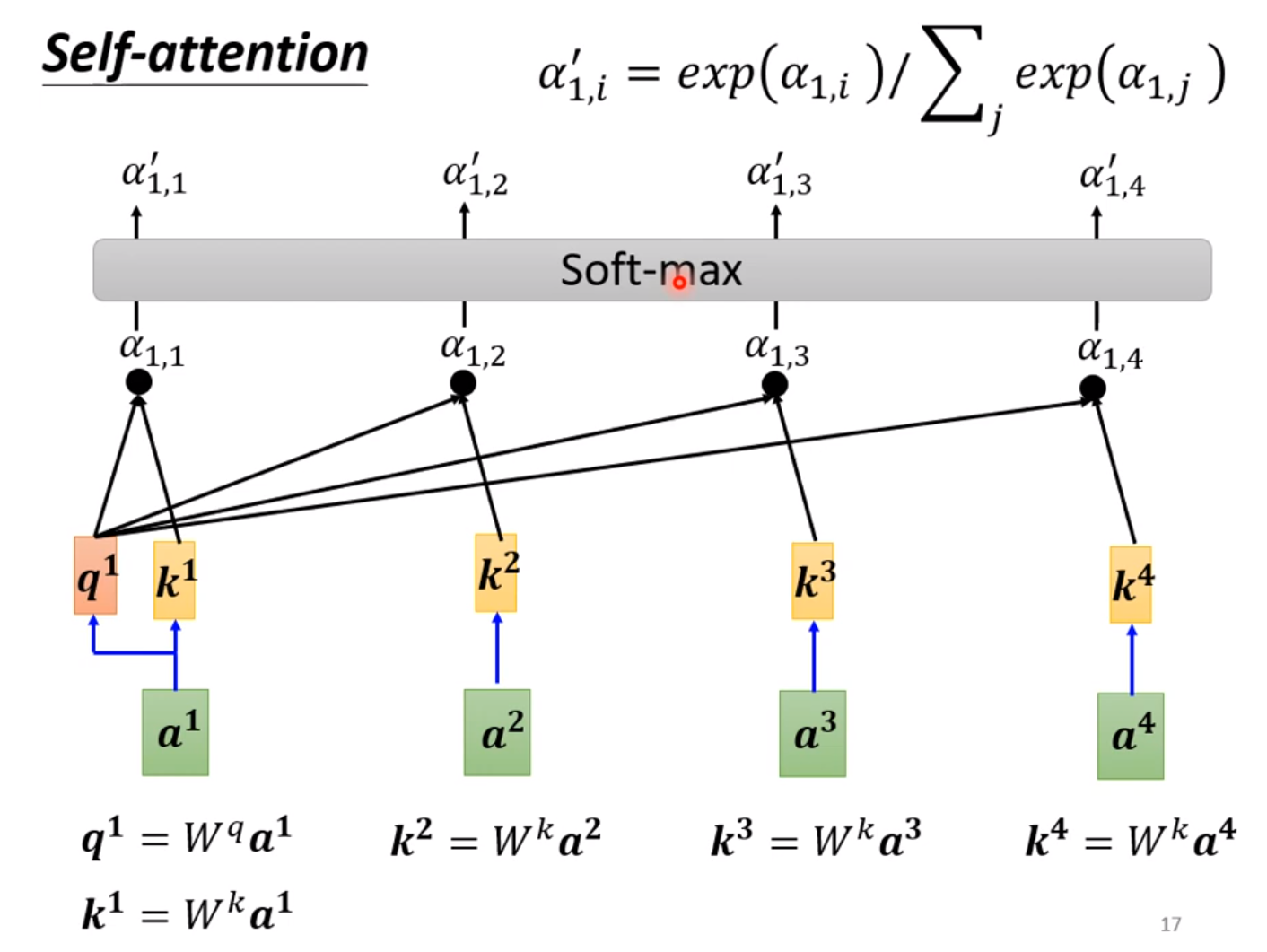
比较常见的是用Dot-product:
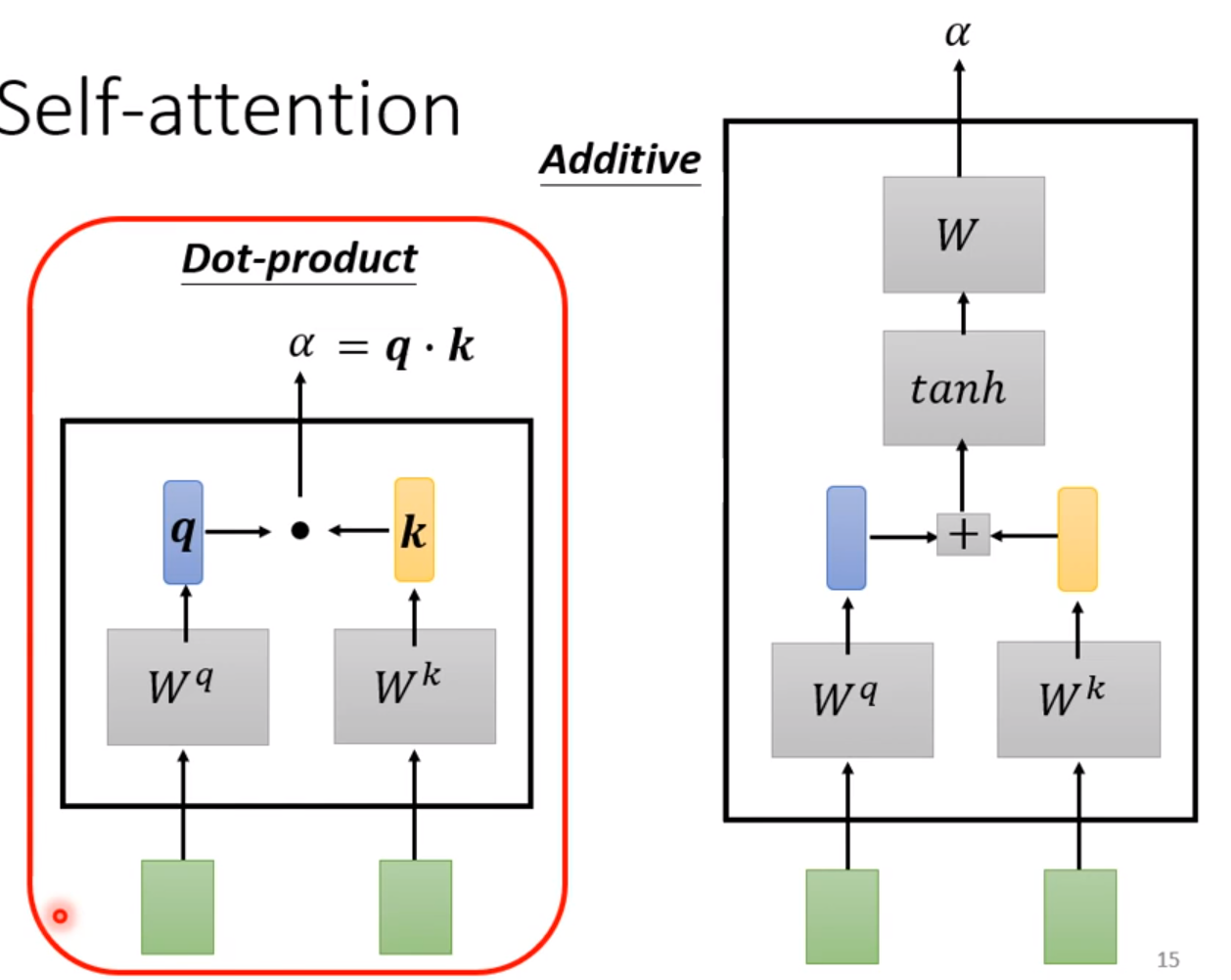
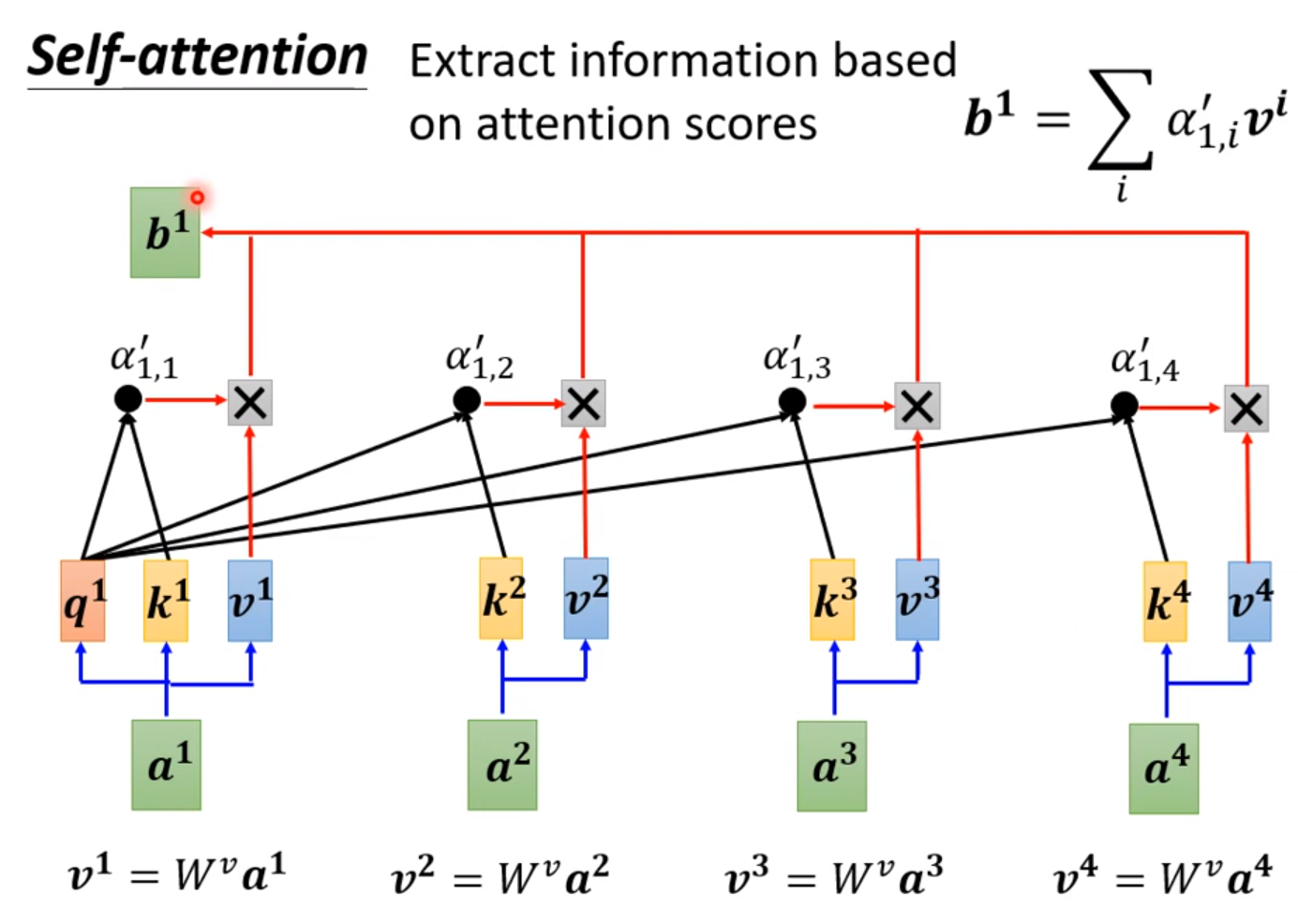
其中里面的参数都可以通过梯度下降法自行调整,如果a1和a2相关性较高,那么a’12就会趋近于1,b1的值也就会趋近于v2。
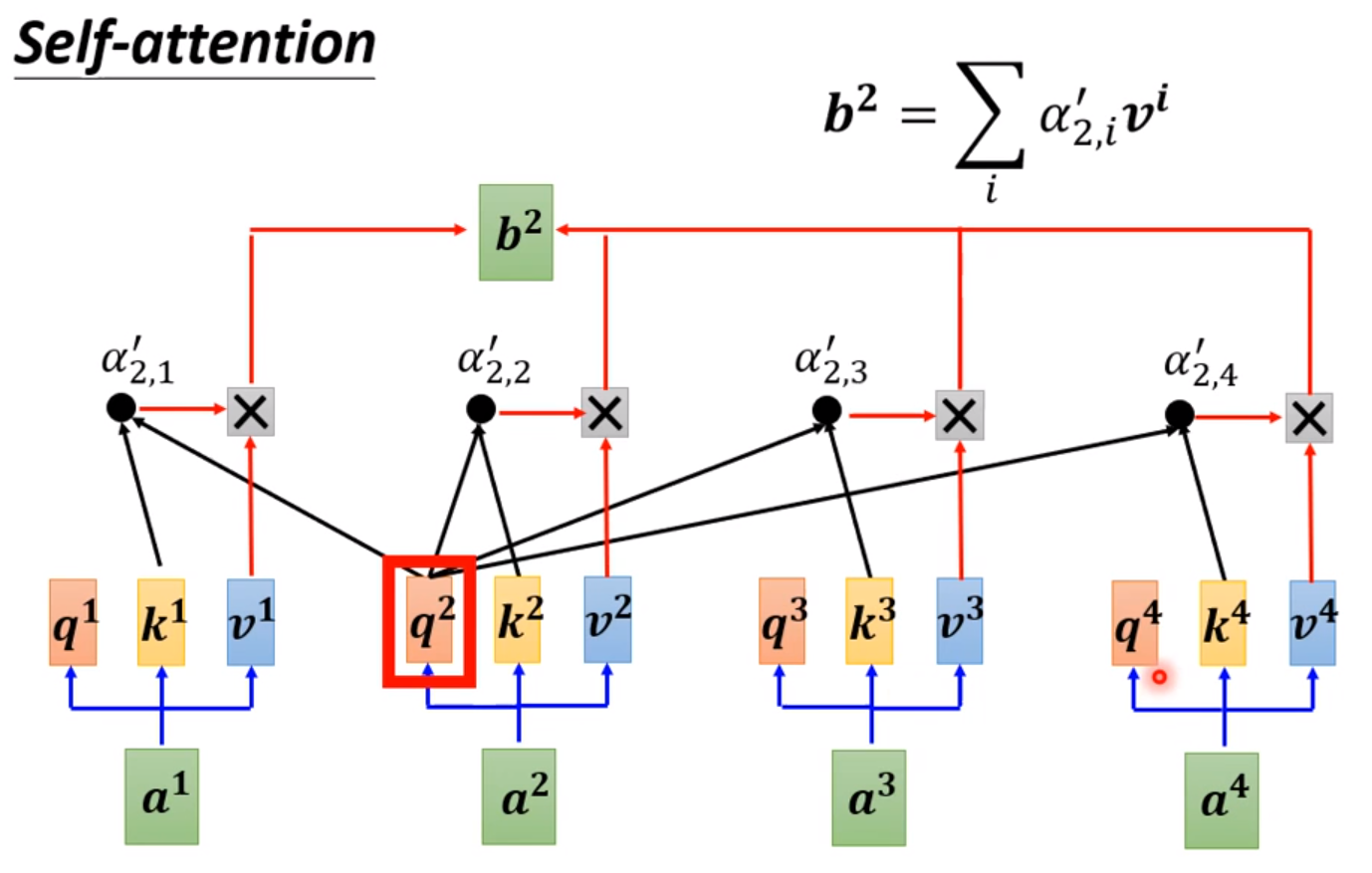
这样重复多次这样的步骤就能计算每个b。
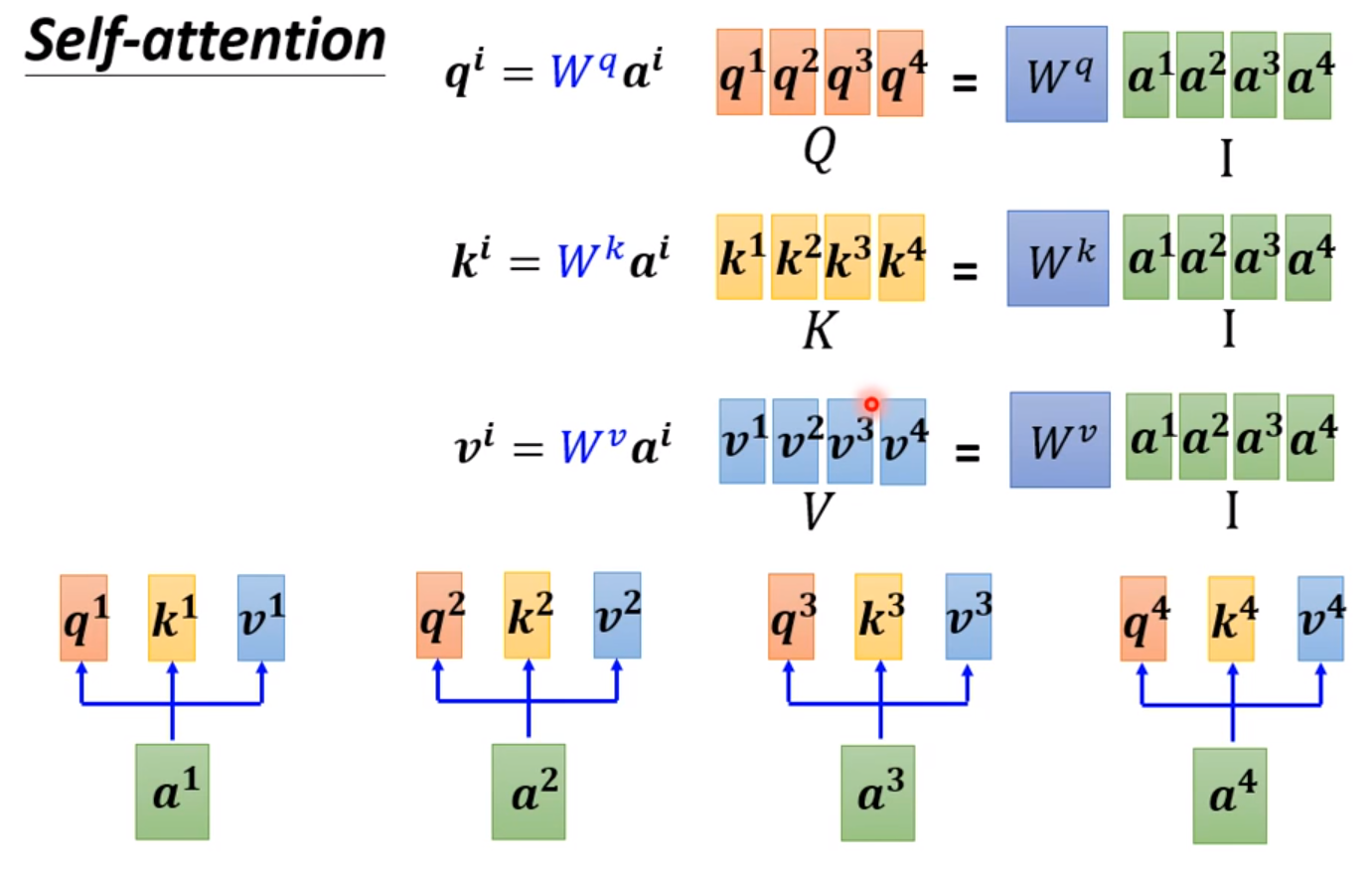

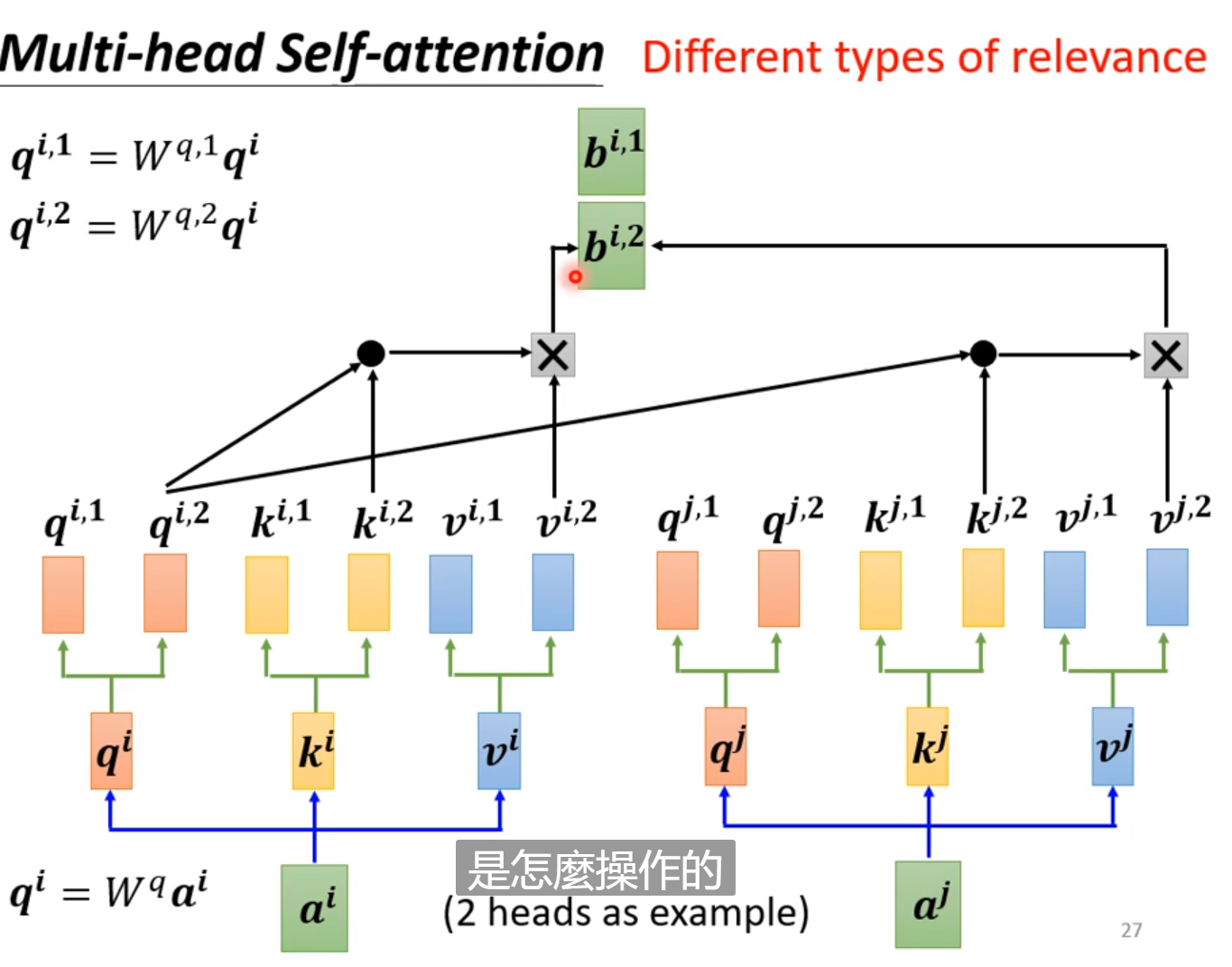
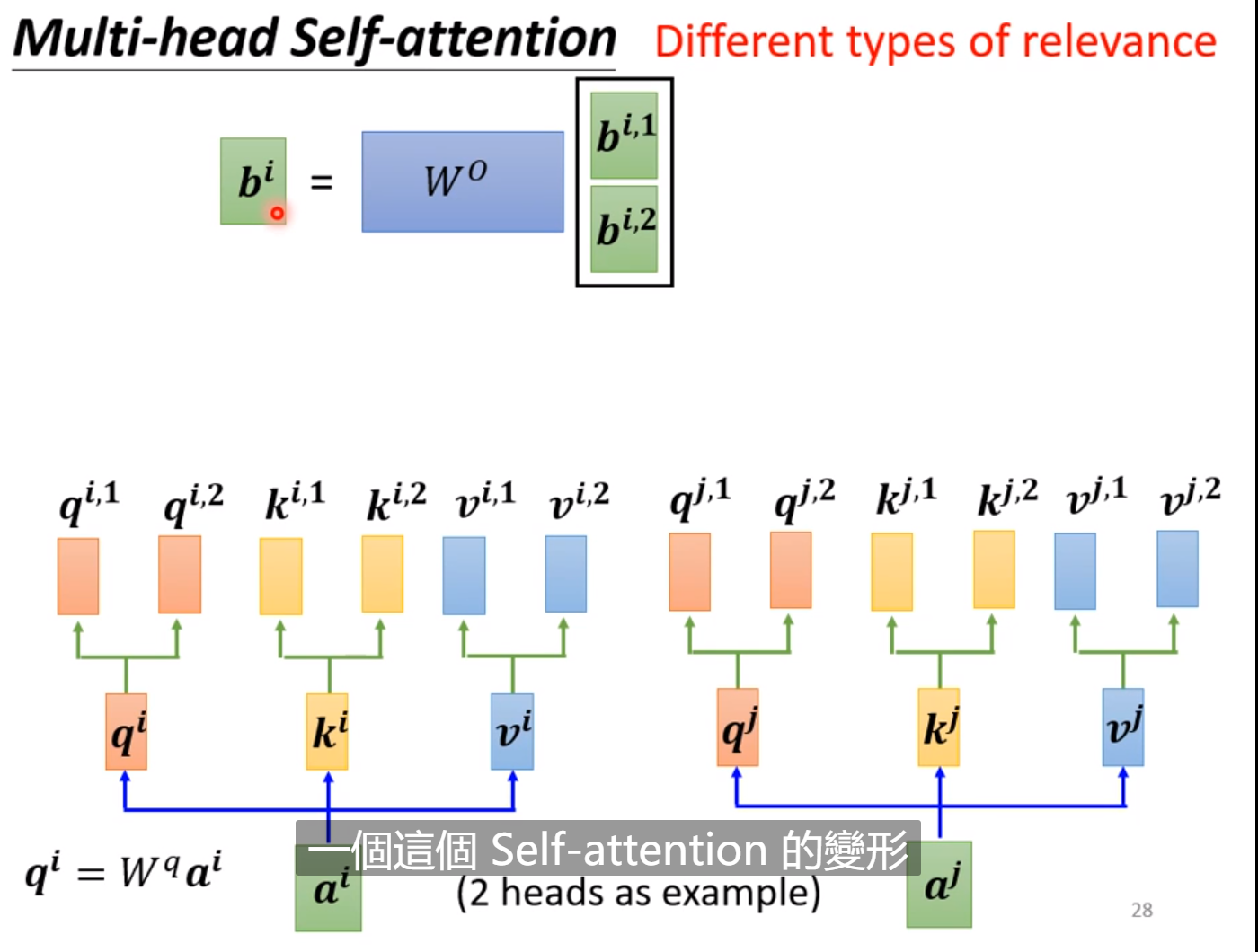
每个输入可以弄更多的q,k,v,一组参数可以看成负责一个相关性,可以得到更好的效果。最后再把多个b进行线性变化变成一个b送到下一层。
这个时候,这个网络是没有位置的信息的,例如输入几个字这个字是在句首句尾是判断不出来的。如果你决定位置信息是分类的重要依据,就要把位置信息加进去,你可以为每一个位置设置不同的Vector,然后把这个信息直接加进输入中就行了。这个Vector是人为设计的,叫做(Positional Encoding),这是尚待研究的问题。
其实CNN是Self-attention的特例,Self-attention设置特定的参数可以做到和CNN一样的事情。
拓展:LSTM(Long Short-term Memory)
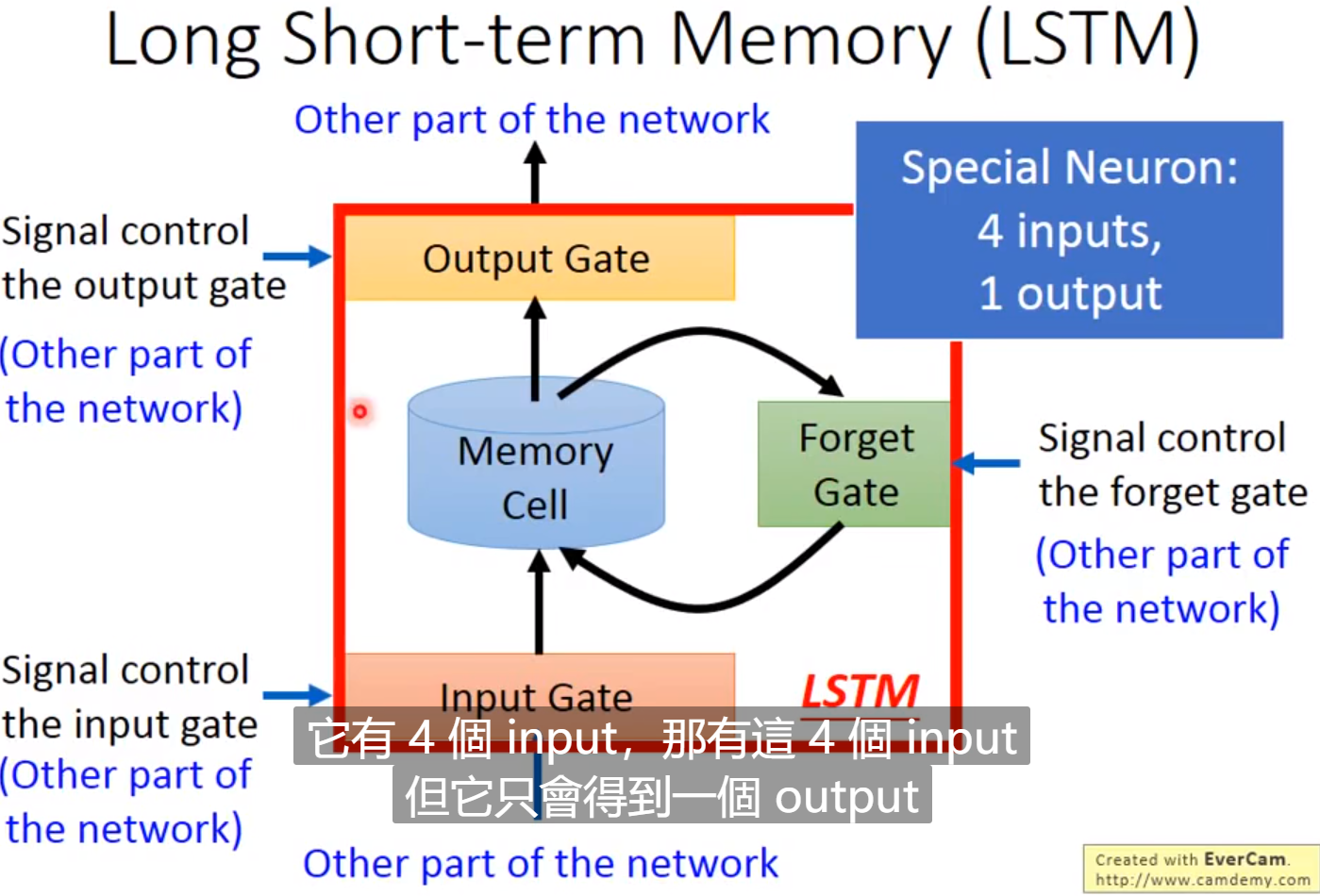
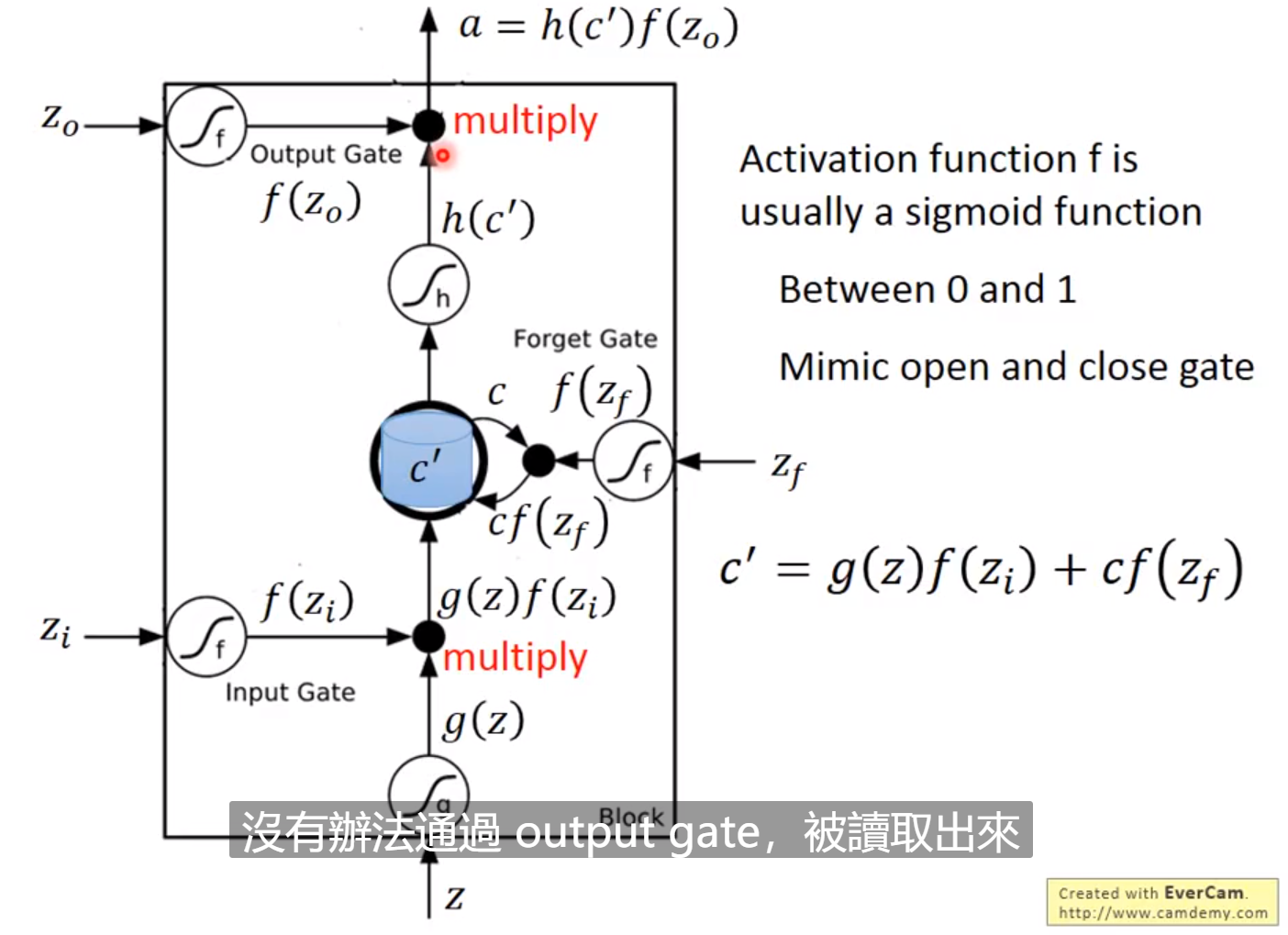
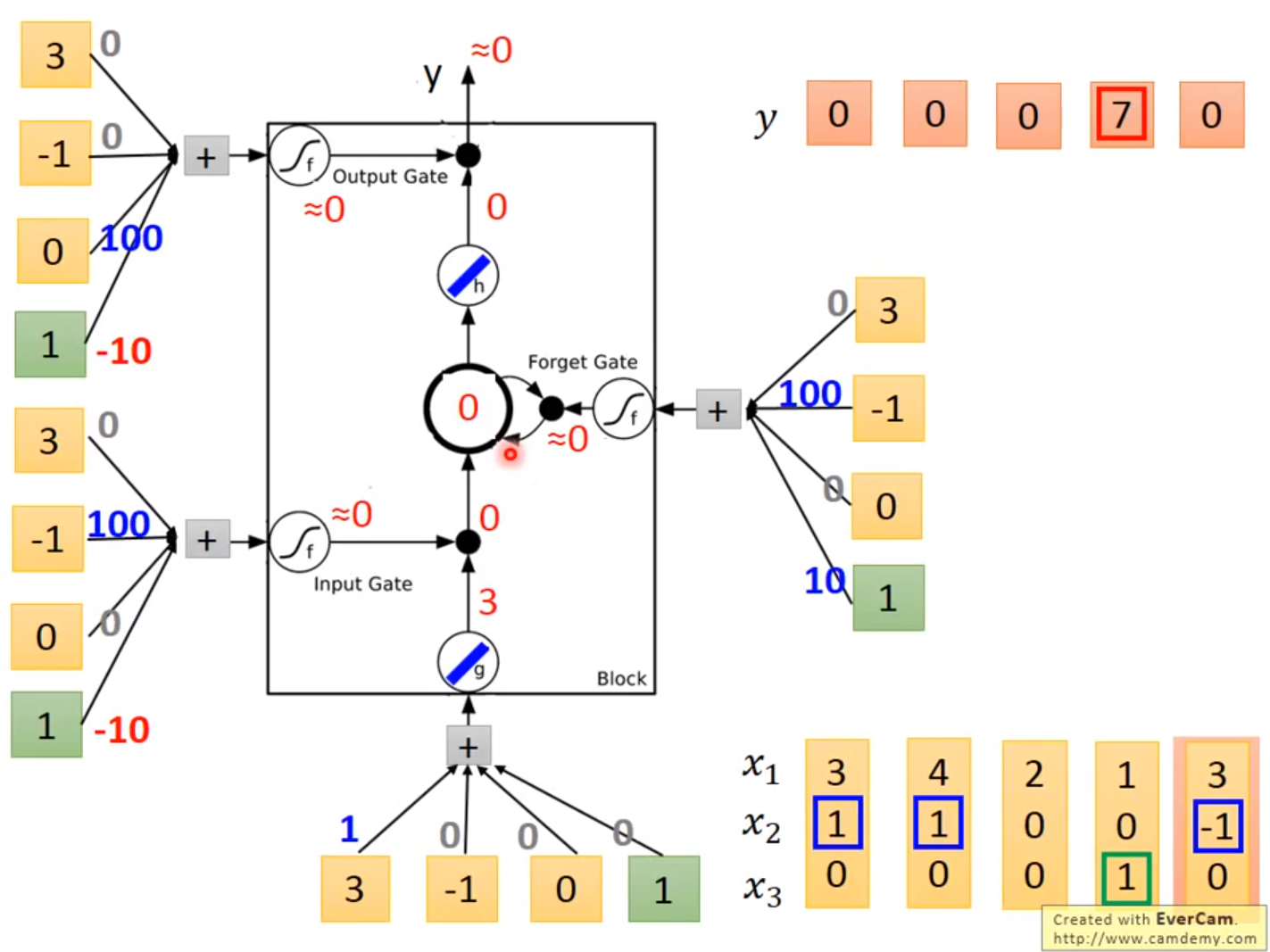
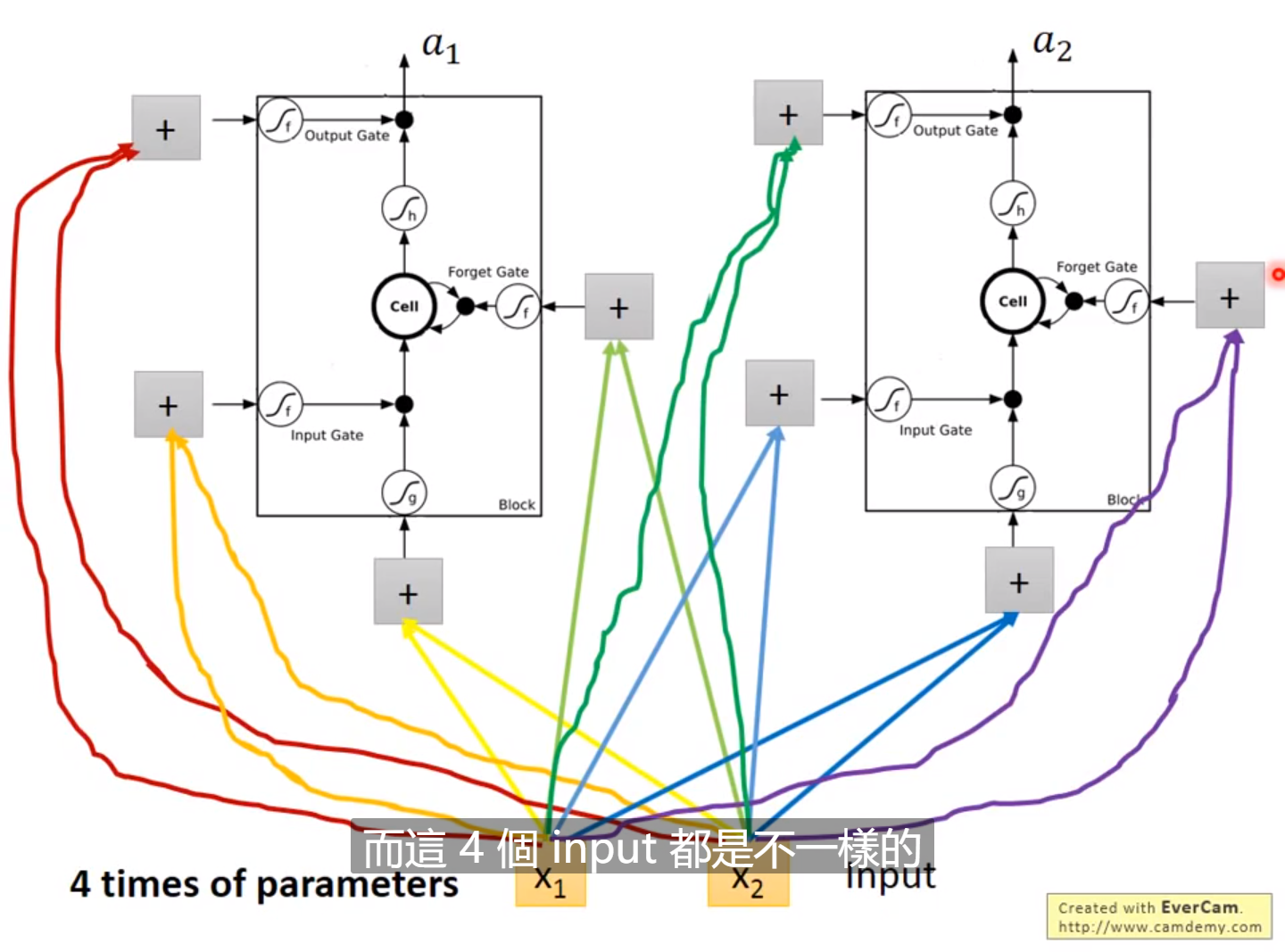
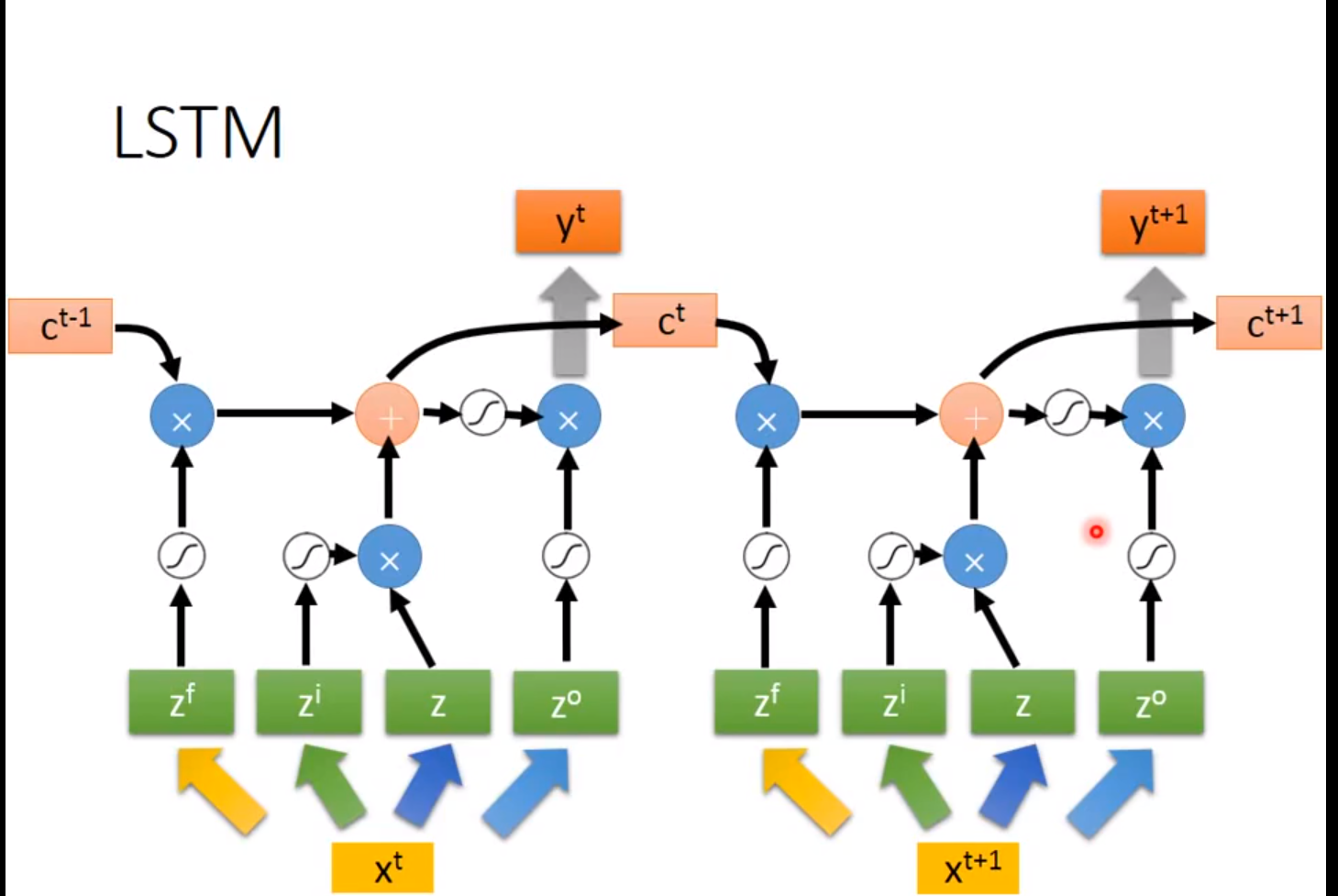
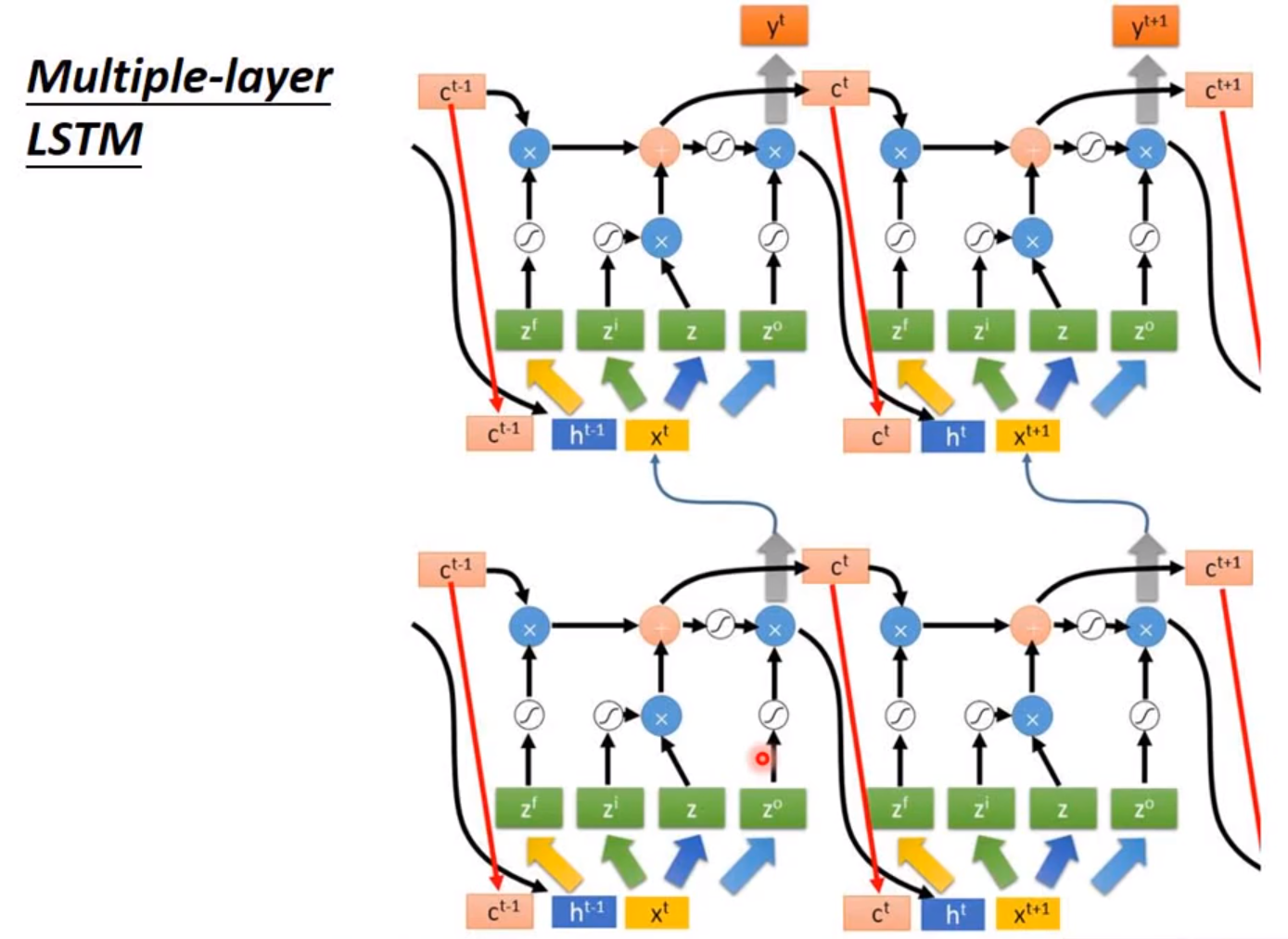
待完善。。。。。。
拓展:GNN(Graph Neural Network)
self Attention 可以用在Graph上面。
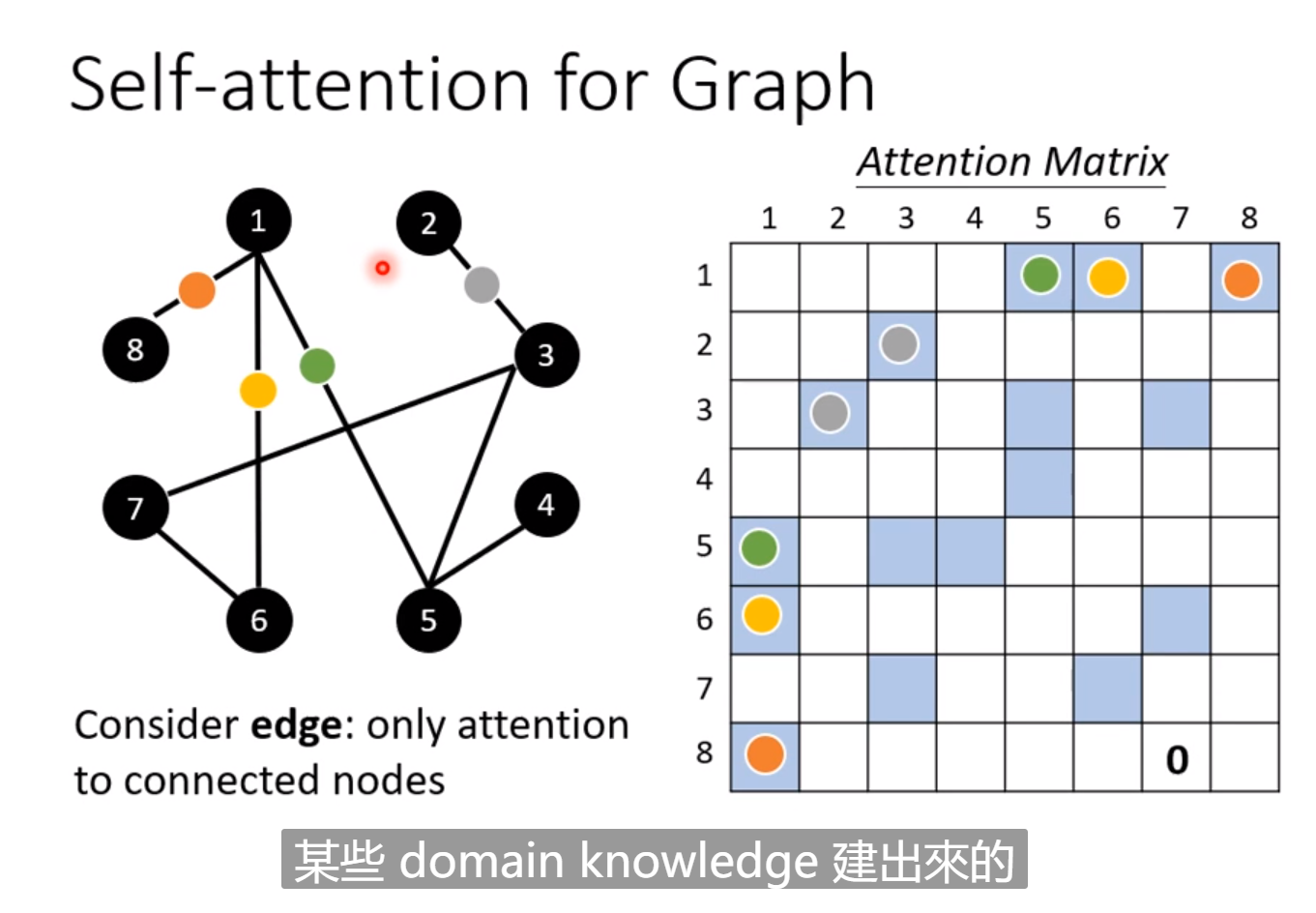
在Graph中输入和输入直接的连接关系是事先就已经订好的,因此我们只需要计算有关系节点之间的α值,没有关系的直接设为0,有关系的再由网络训练得到具体的数值。
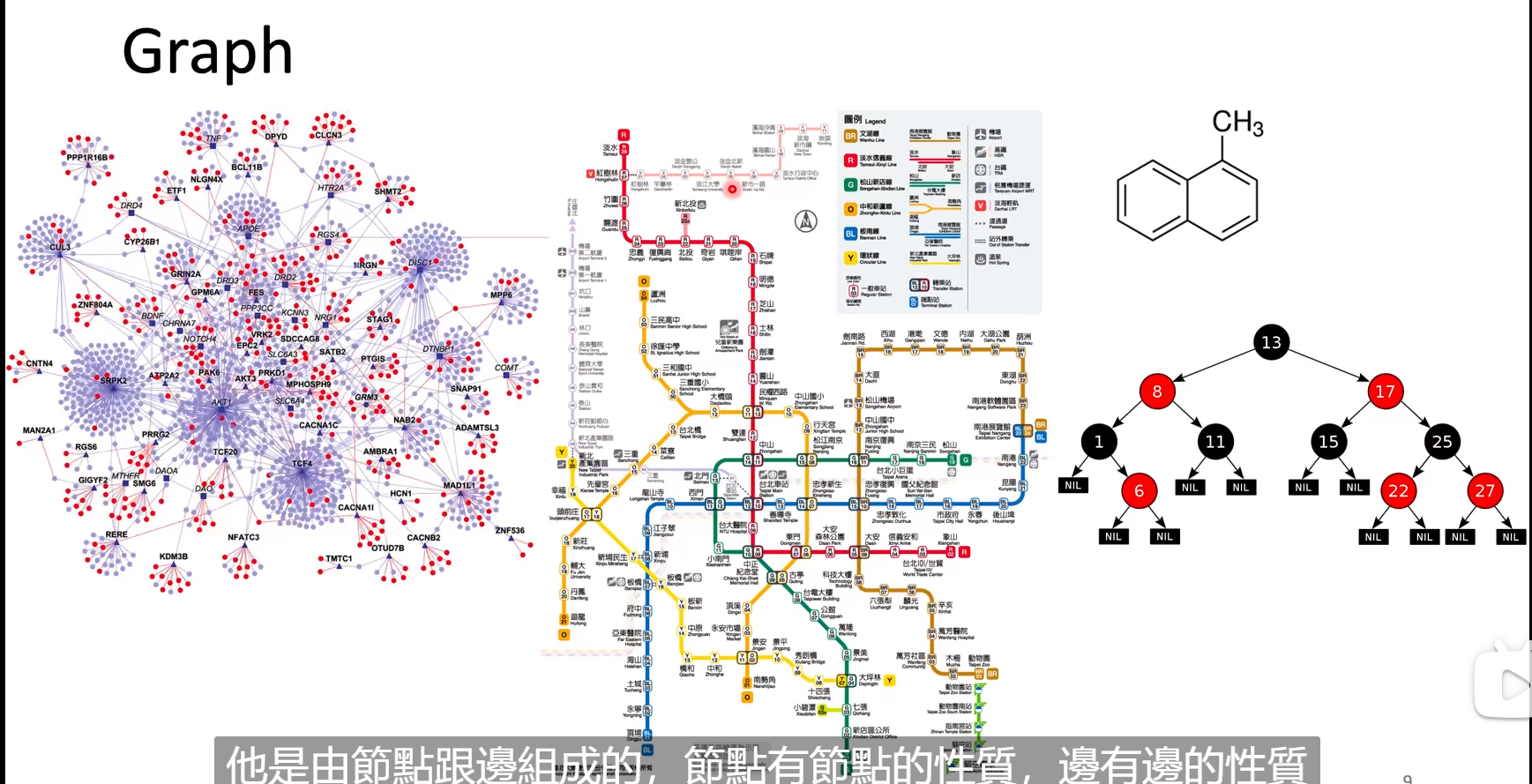
待完善。。。。。。。
研究领域:(Unsupervised Learning:Word Embedding)

在NLP领域,如果每个词都用一个one-hot向量来表示会导致输入的维度过大,计算量过大,并且没有办法表示词与词之间的关系,我们倾向于把它们映射到一个更小维度的向量中,这个向量是比较连续的,它们直接的距离就代表了相关性。这是一种聚类,无监督学习。
首先这个算法需要阅读大量的文章。如果两个词语常常一起出现,那它们的距离会比较接近,因此我们会尽量找两个向量使它们接近,这就是Count based。还有一种叫做Prediction based。我们输入前一个单词的one-hot向量,通过模型计算下一个最有可能出现的单词,输入的one-hot向量可以用过线性变化转换为更低维的稠密的向量,进行输入,通过大量的文章的学习,由于这两个不同输入的学习到的输出是相近的,因此这个稠密的向量在梯度下降法的学习下会变得更加相近。
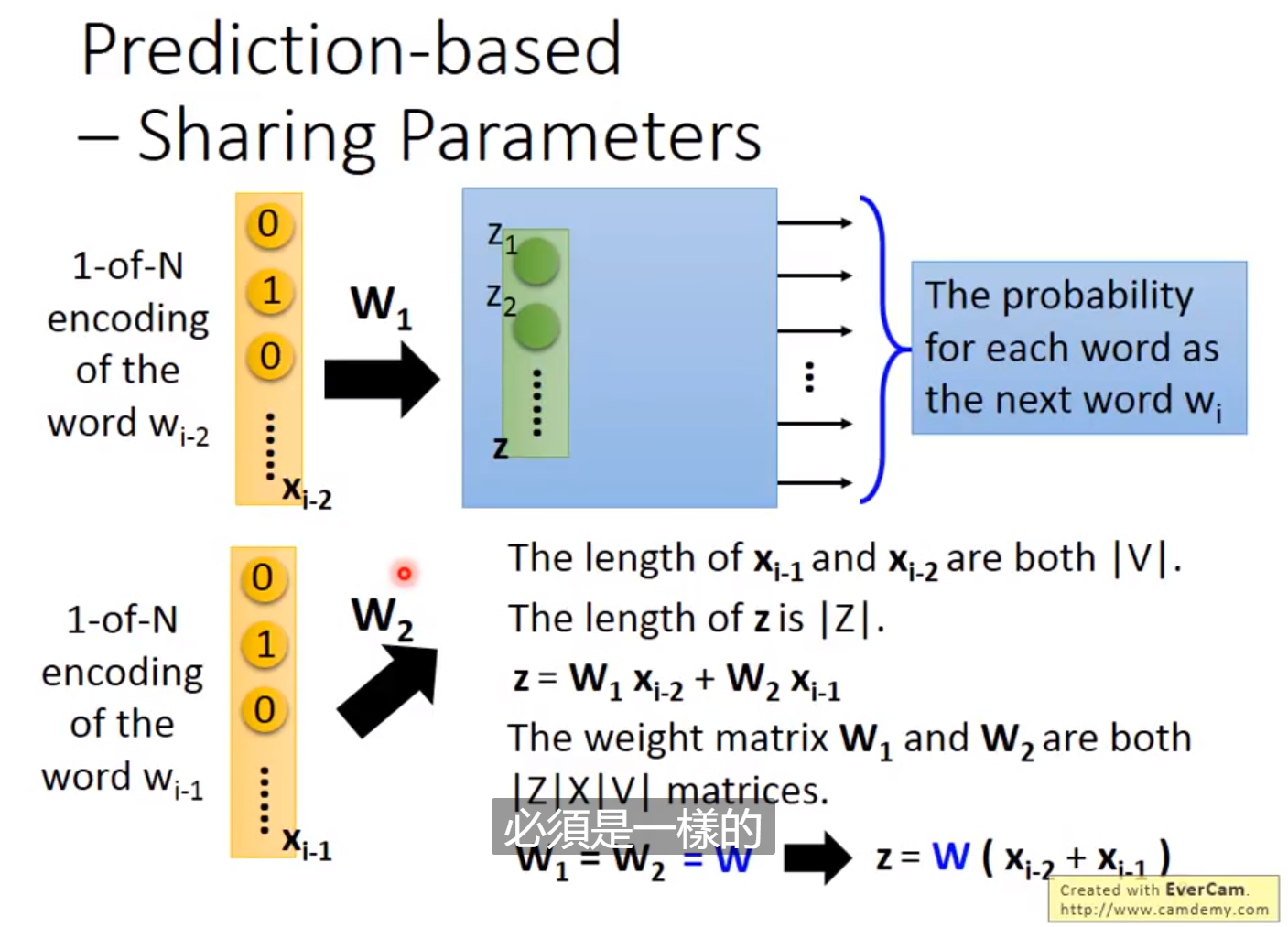
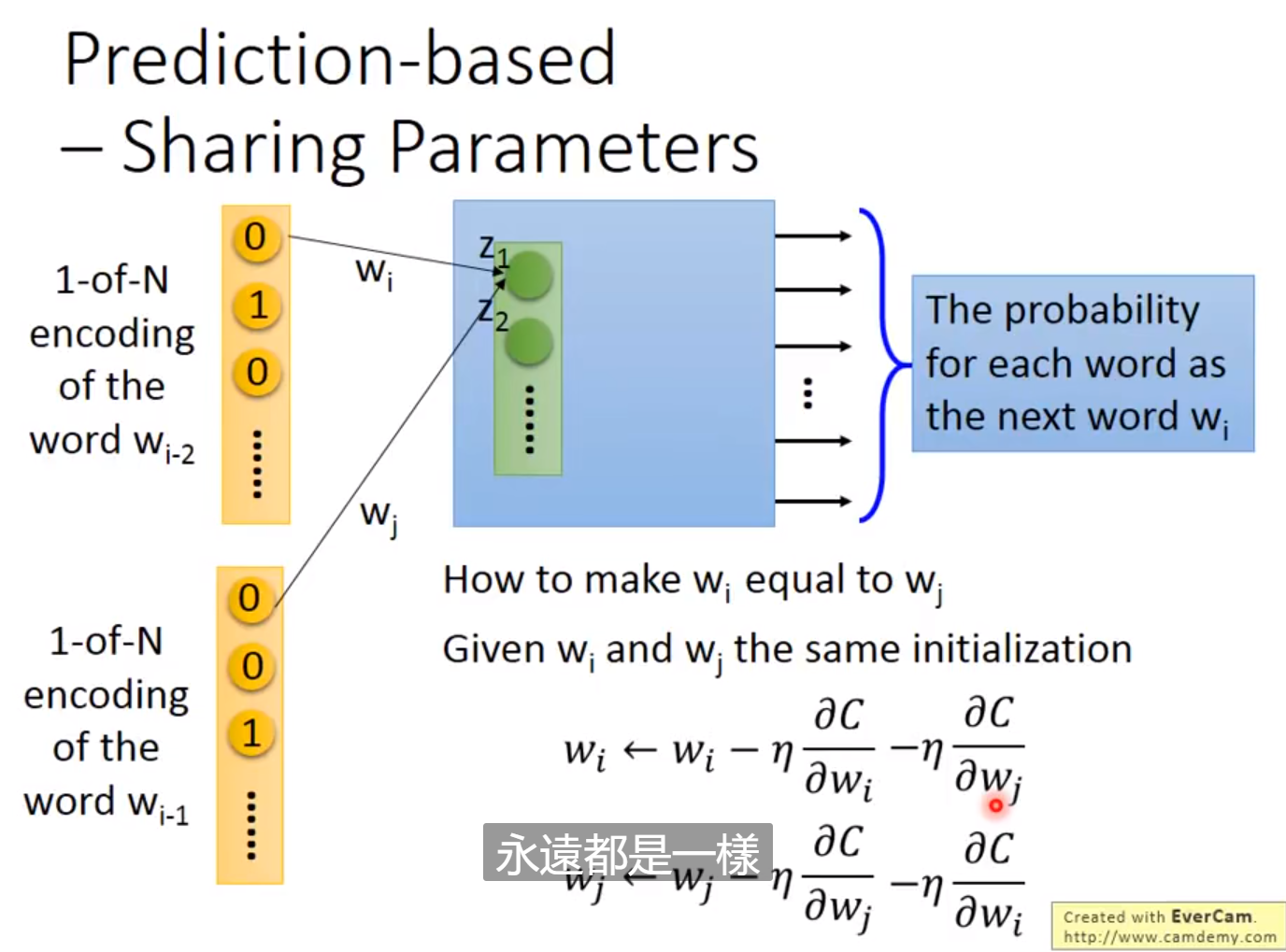
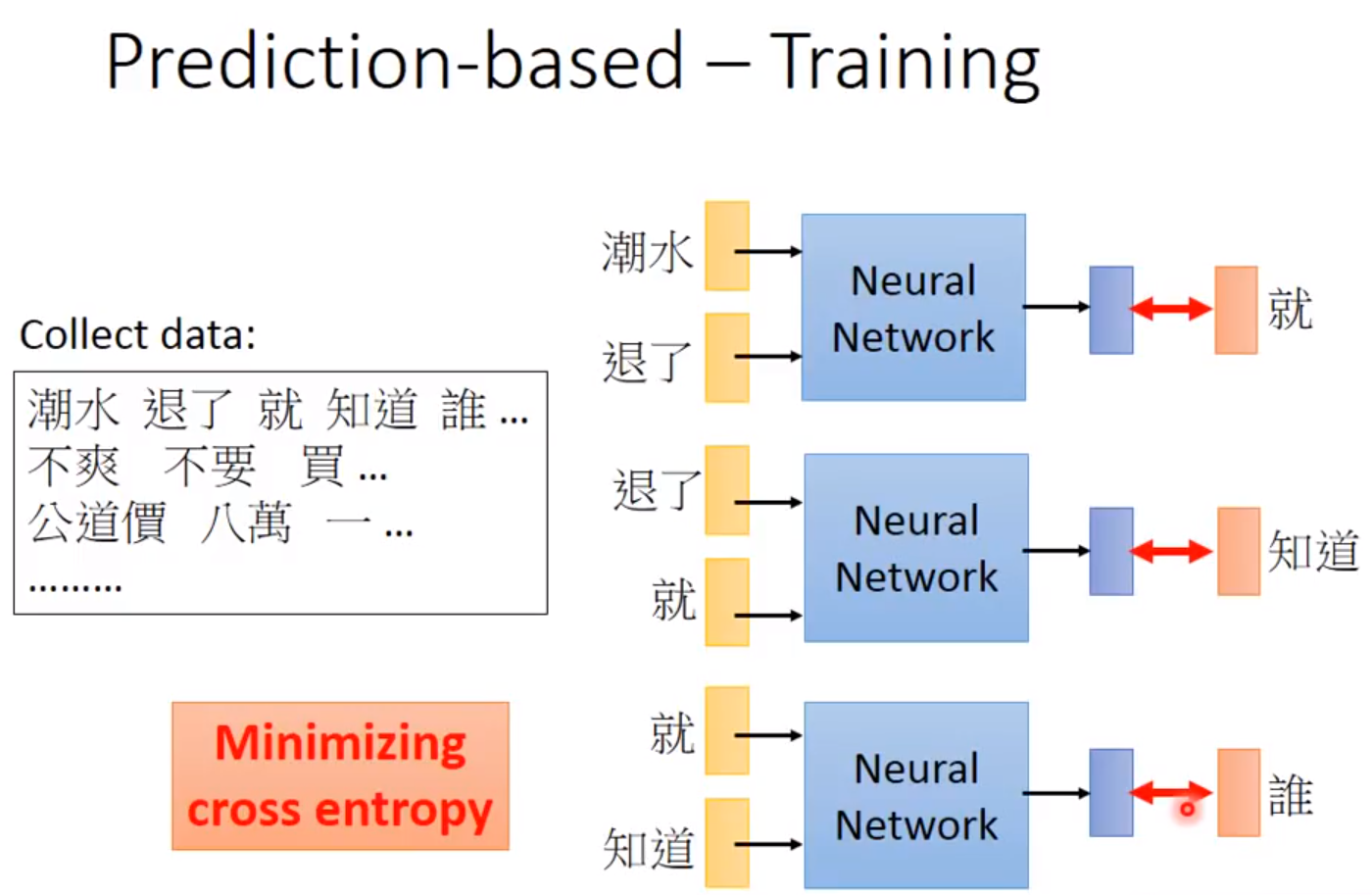
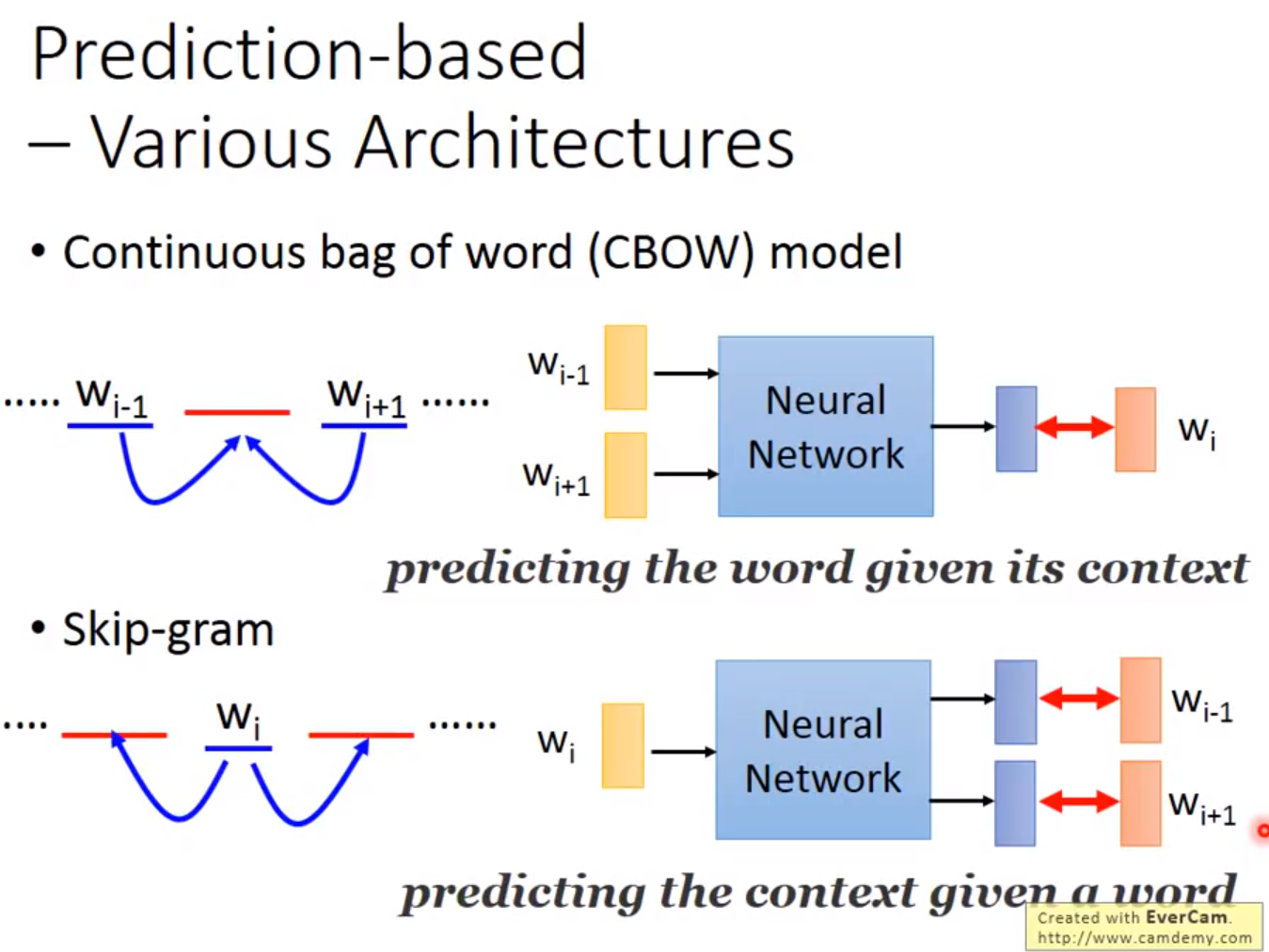

待完善。。。。。。。。。。。。
Transformer
Transformer的中文意思是变形金刚,它是一个sequence-to-sequence的model,也就是说输入是一个序列,输出也是一个序列,但我们不知道输出序列的长度。一个应用是语音辨识。输入语音信号所转换的Vector,输出对应的文字。输入的长度和输出的长度没有绝对的关系。另一个是机器翻译,输入一个语言的句子,输出另一个语言的句子。还有一个是语音翻译,例如声音讯号是英文,输出的是中文的文字,这在对于有些没有文字的语言尤其适用。许多问题都可以用sequence-to-sequence的方法硬做,例如给一个句子分析语法结构。又例如给机器一张图片,把图片中所有物体选出来分类。

一般的sequence-to-sequence分为两块,一块Encoder,一块Decoder。
Encoder的作用是输入一排向量,输出另外一排个数相同的向量,用的是self-attention。
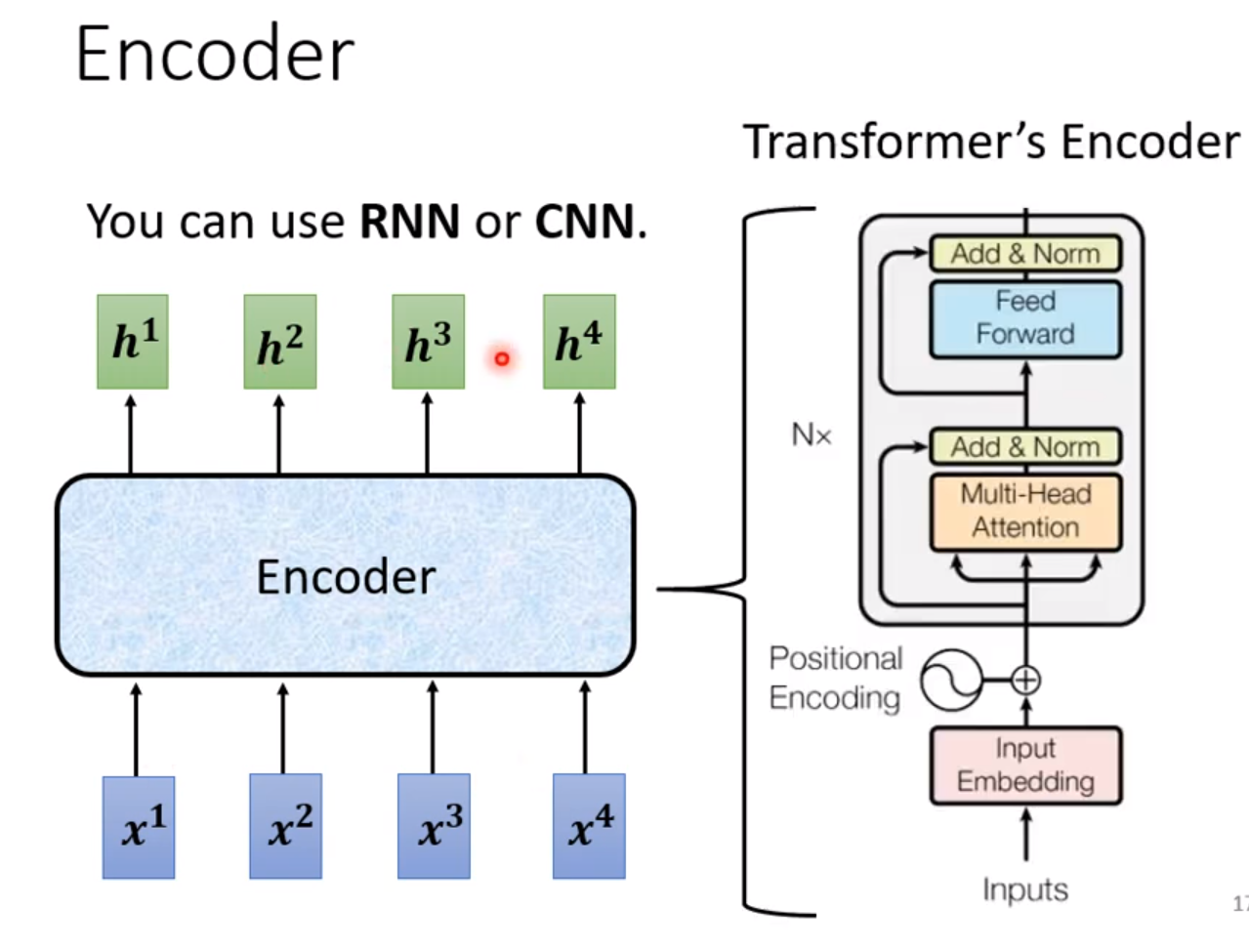
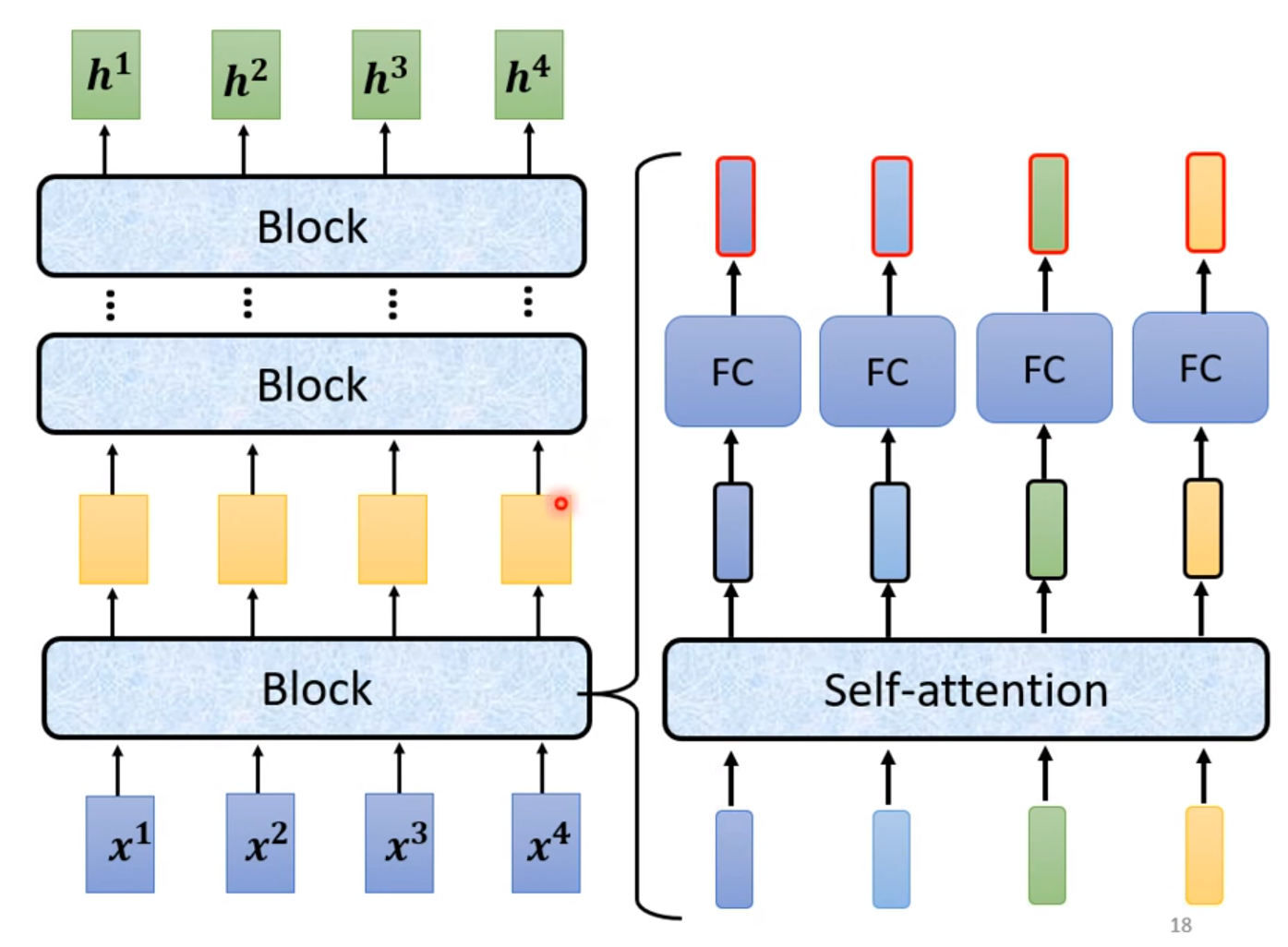
其中一个Block包含着一个Self-attention和一个fully-connectted,但实际上Transformer还要更复杂一些。
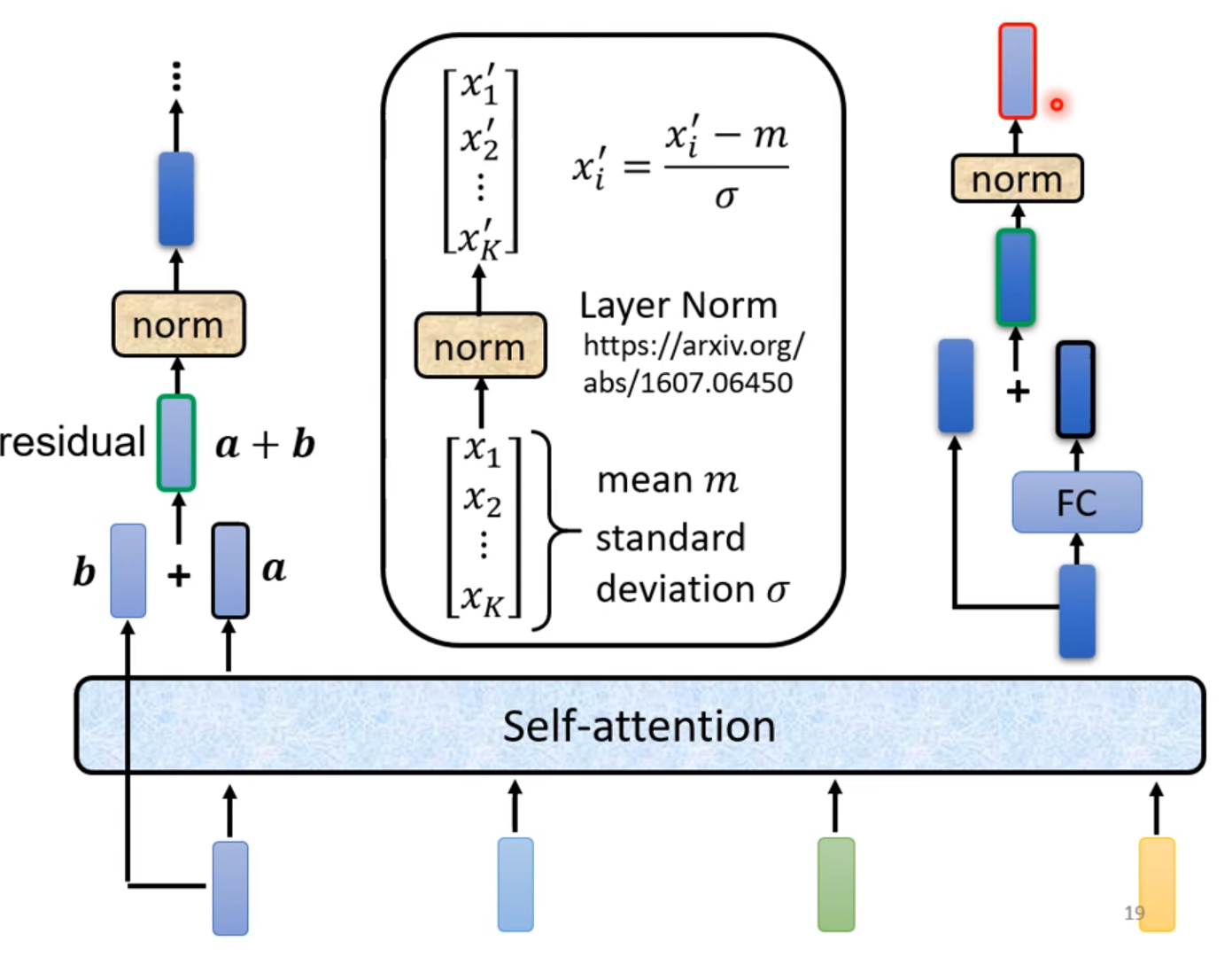
在Transformer的Block中,self-attention和fully-connected都要进行残差连接(residual connection),然后还要进行标准化normalization映射到(0,1)分布,注意这里做的是layer-normalization而不是batch-normalization。同时在输入之前还要加上Input-Embedding来进行词嵌入,然后进行Positional-Encoding来加入位置信息。
接下来讲解Decoder的部分,这里有两种,着重介绍Autoregressive(自回归)的Decoder。首先我们需要把Encoder的信号读进去,然后给一个开始信号,输出一个结果,然后把这个结果作为下一次的输入来尝试下一个输出,这样反复下去。
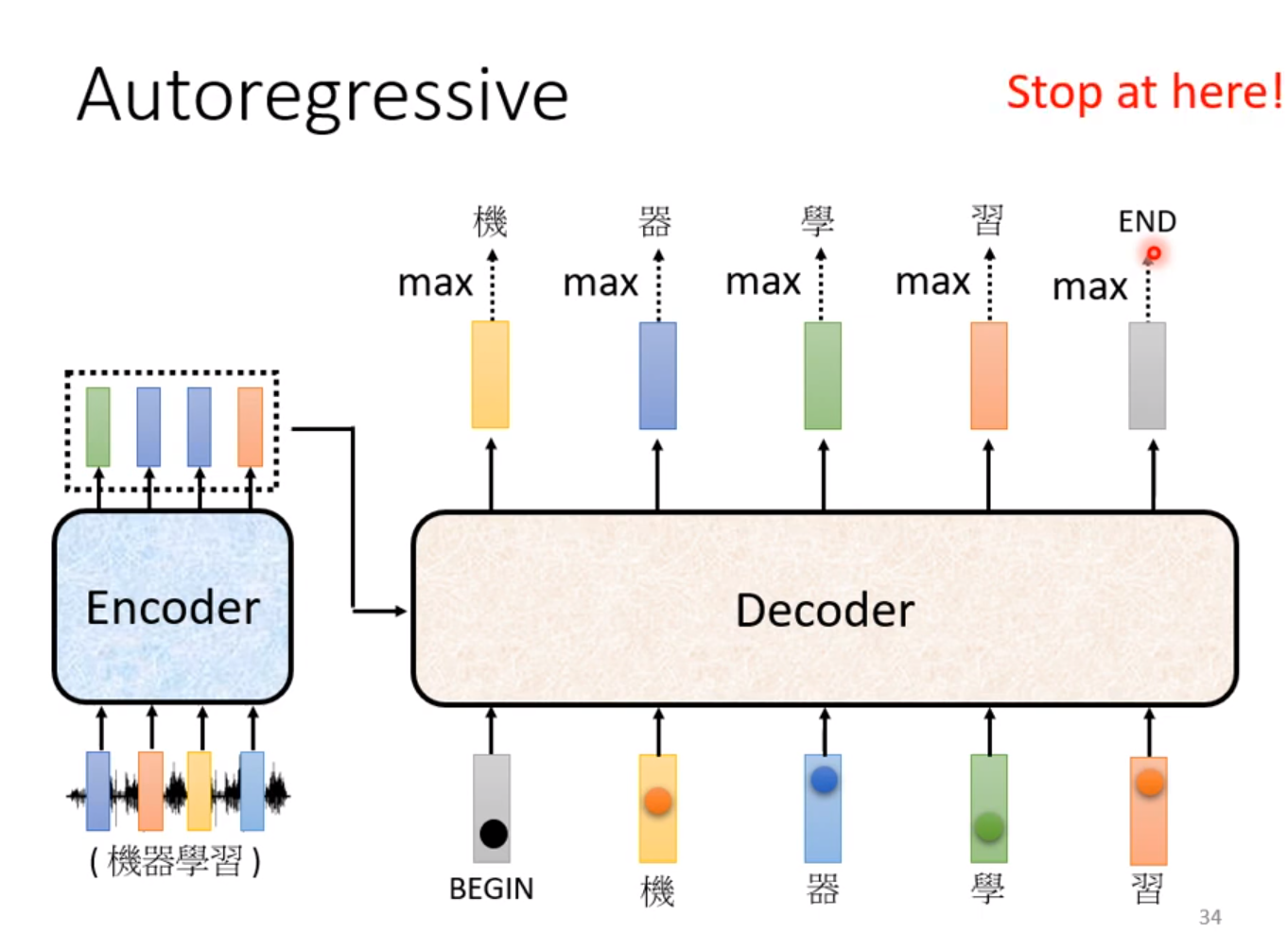
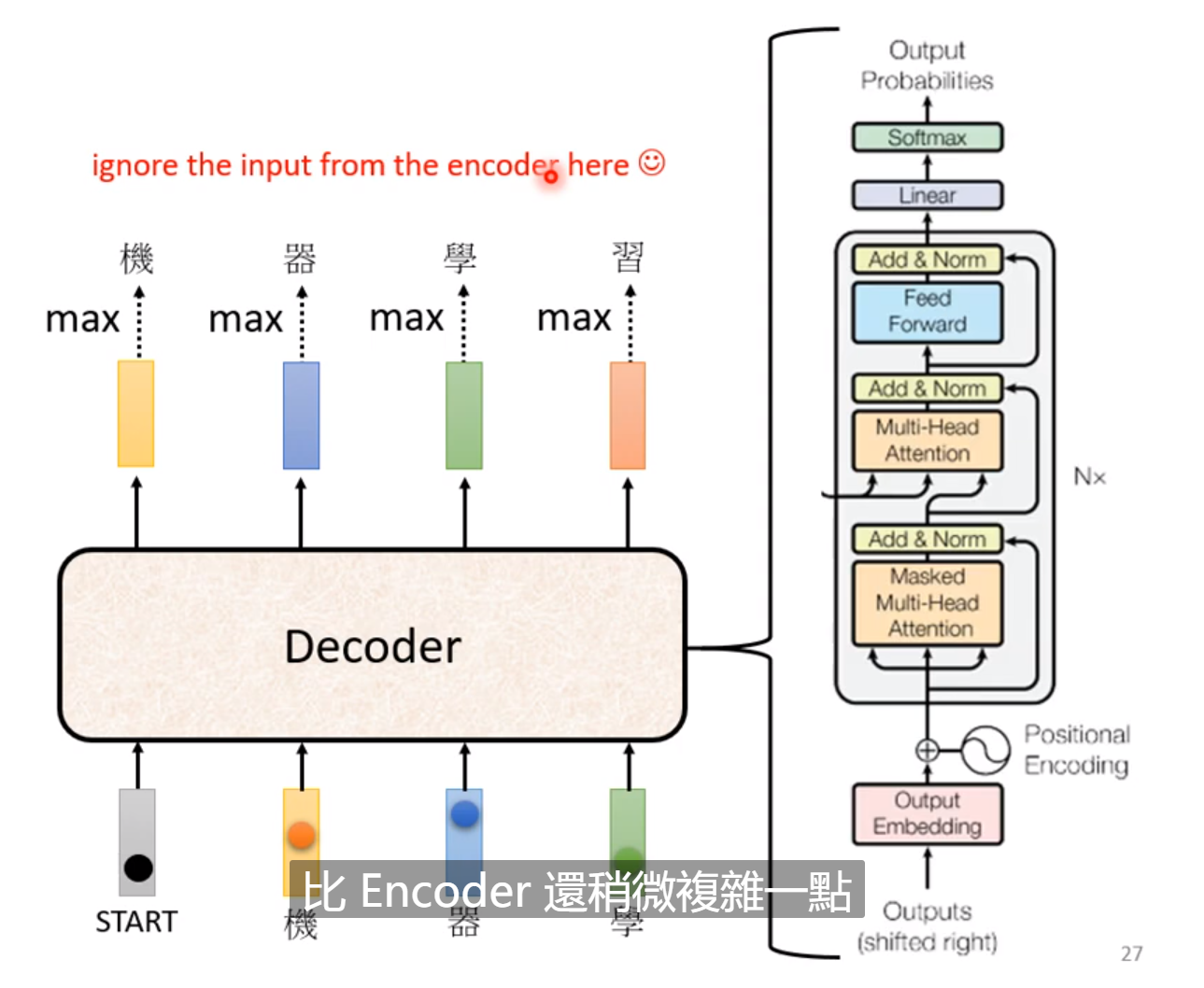
可以看到Encoder和Decoder的区别不是很大,其中中间多了一个步骤,self-attention也略有不同。
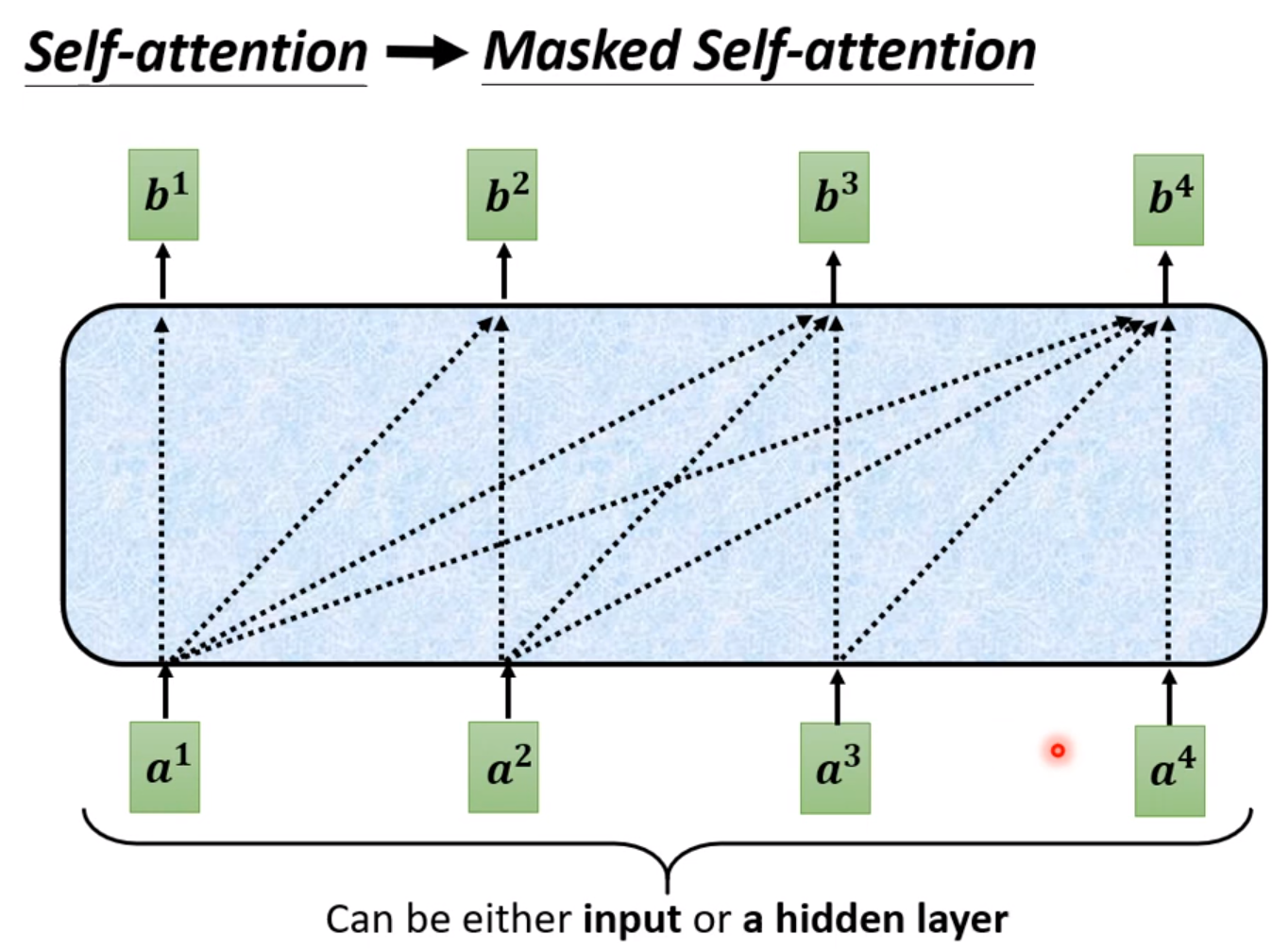
也就是说Masked-Self-attention不能像self-attention一样每个b1都由四个a决定,b只由前面的a决定而不能受后面的a影响。以b2为例:

这是由于前一个的输出当做后一个的输入。所以在计算b的时候根本不能把后面的a考虑进来,因为只有计算了前一个b才存在后一个a。
接下来的问题是确定输出的长度。为了让输出停下来,我们需要确定终止符,当输出的向量为这个终止符时,不再继续输出结果,这个终止符和起始符可以共用一个向量。这就是Autoregressive-Decoder的运作方式。
如果是Non-Autoregressive的Decoder(NAT)。我们可以一次性输入一排的起始符来产生一排输出。但是没有办法知道应该输出几个字,需要另外的Classifier来输入Encoder的输入产生一个数字的输出决定Decoder的输入输出序列的长度。或者另外的处理办法是假设输出的长度不大于300,可以令输入序列为300个起始符,当输出产生终止符时则忽略后面的输出。
NAT的好处是不用一个个字产生结果,一个步骤产生完整句子,速度比AT要快,而且能够控制输出的长度。但是AT的表现往往比NAT要好。
然后接下来是Decoder的下一个部分,也是和Encoder最大的不同之处,这是连接Encoder和Decoder的桥梁。其中的两个输入来自Encoder一个输入来自上一个Masked-Self-attention块。
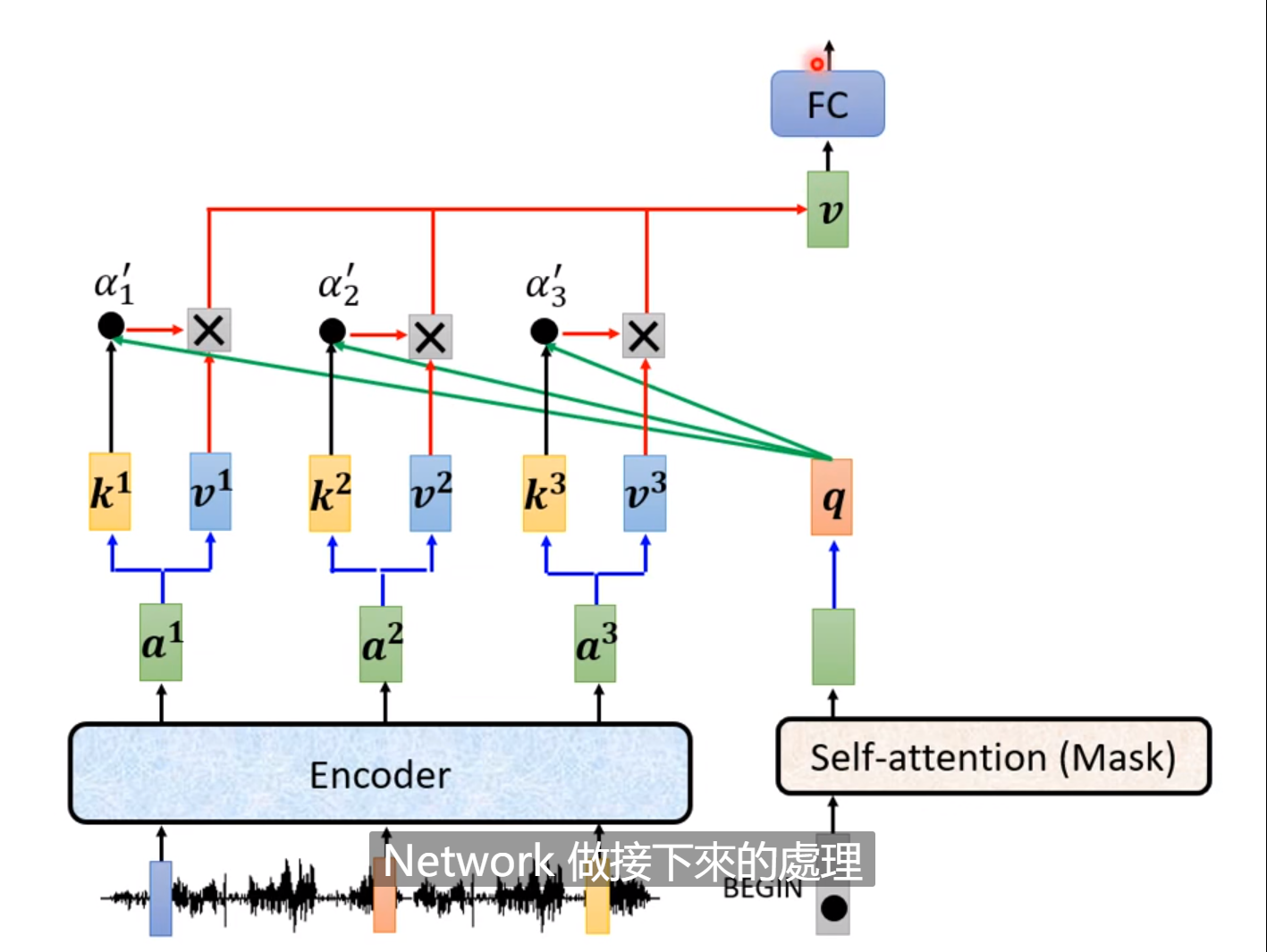
上图就是Muti-head-Attention的运作过程,Encoder输出序列中的每一个输出都通过线性变换产生两个输出,然后和q做cross-attention,这也是一种self-attention,输出一个向量,然后再把这个向量丢到下一个线性层进行处理。然后把最后的输出结果再丢进Decoder做相同处理。
在训练的时候:
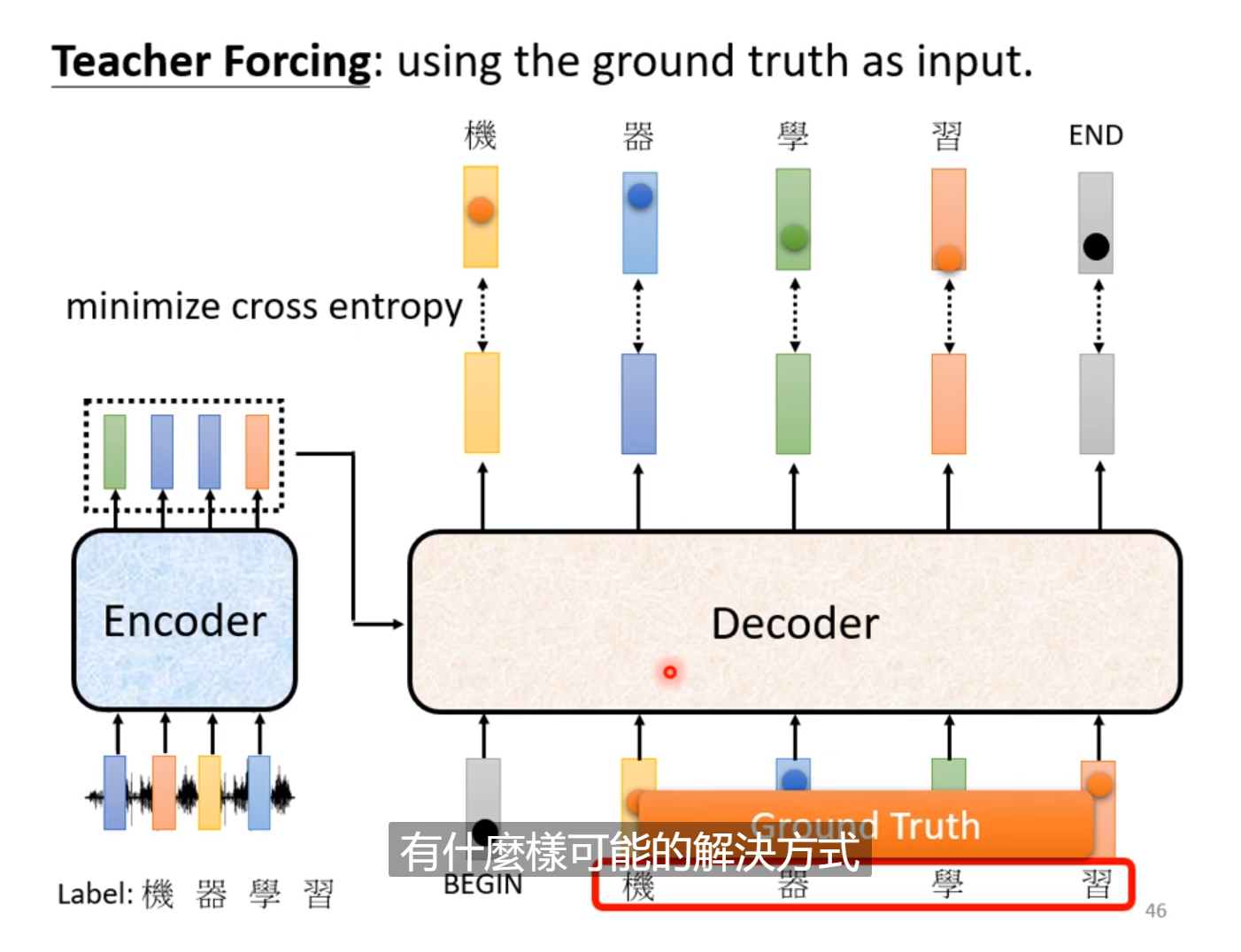
有的时候,例如聊天机器人,输出的语句只需要从输入中复制,这样训练较为容易:

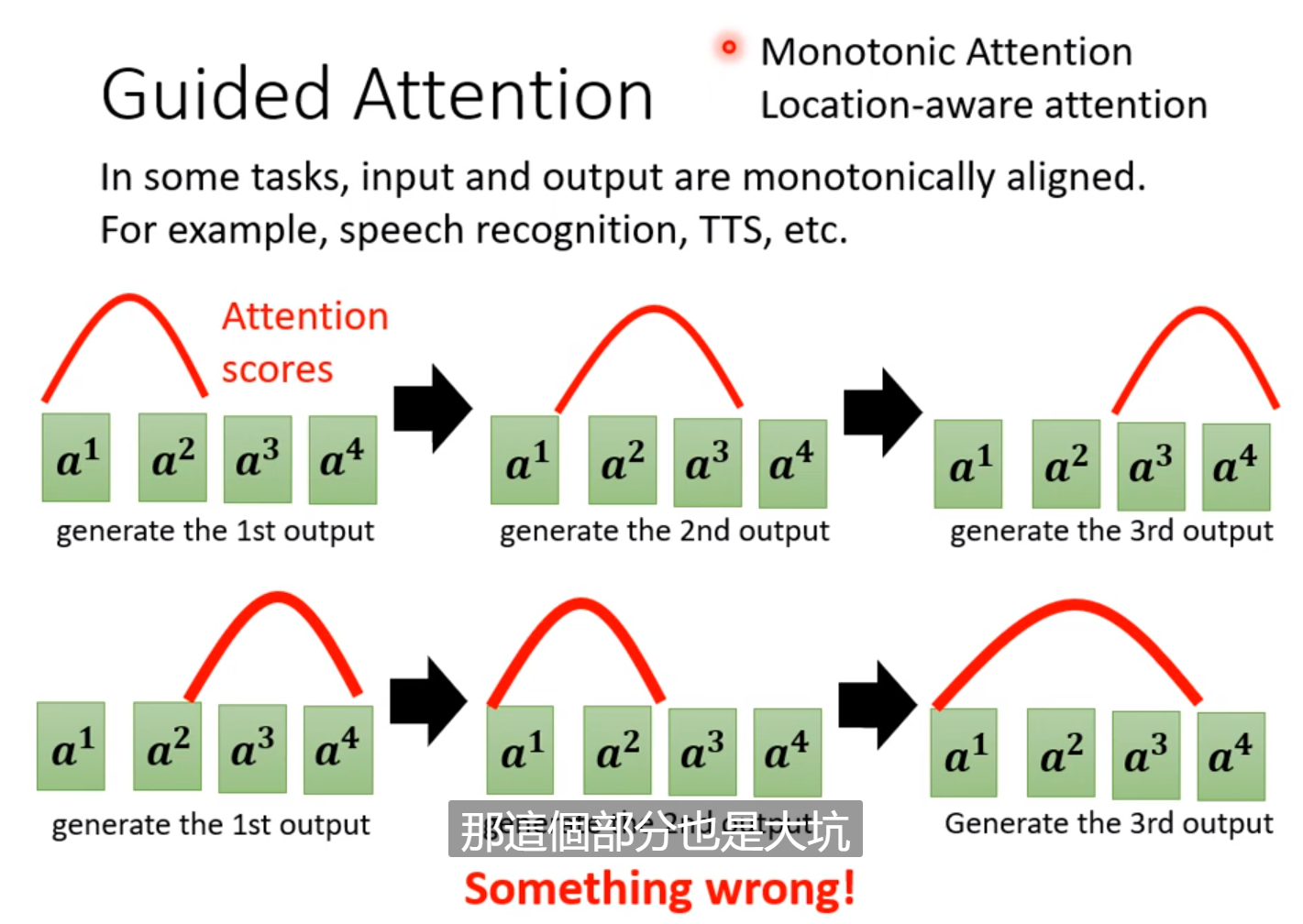


生成对抗网络(GAN)
自监督式学习(Self-supervised Learning)
强化学习(Reinforcement Learning)
这几部分的内容是我的特别是RL是我的研究重点,我另开文章进行叙述。



