卡尔曼滤波器是一种最优化递归数字处理算法(Optimal Recursive Data Processing Algorithm),更像是观测器。应用十分广泛,特别是在导航中。这是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
原因是世界存在非常多的不确定性。一是不存在完美的数学模型,二是系统的扰动往往是不可控的,也很难建模的。三是传感器本身存在误差。
递归算法

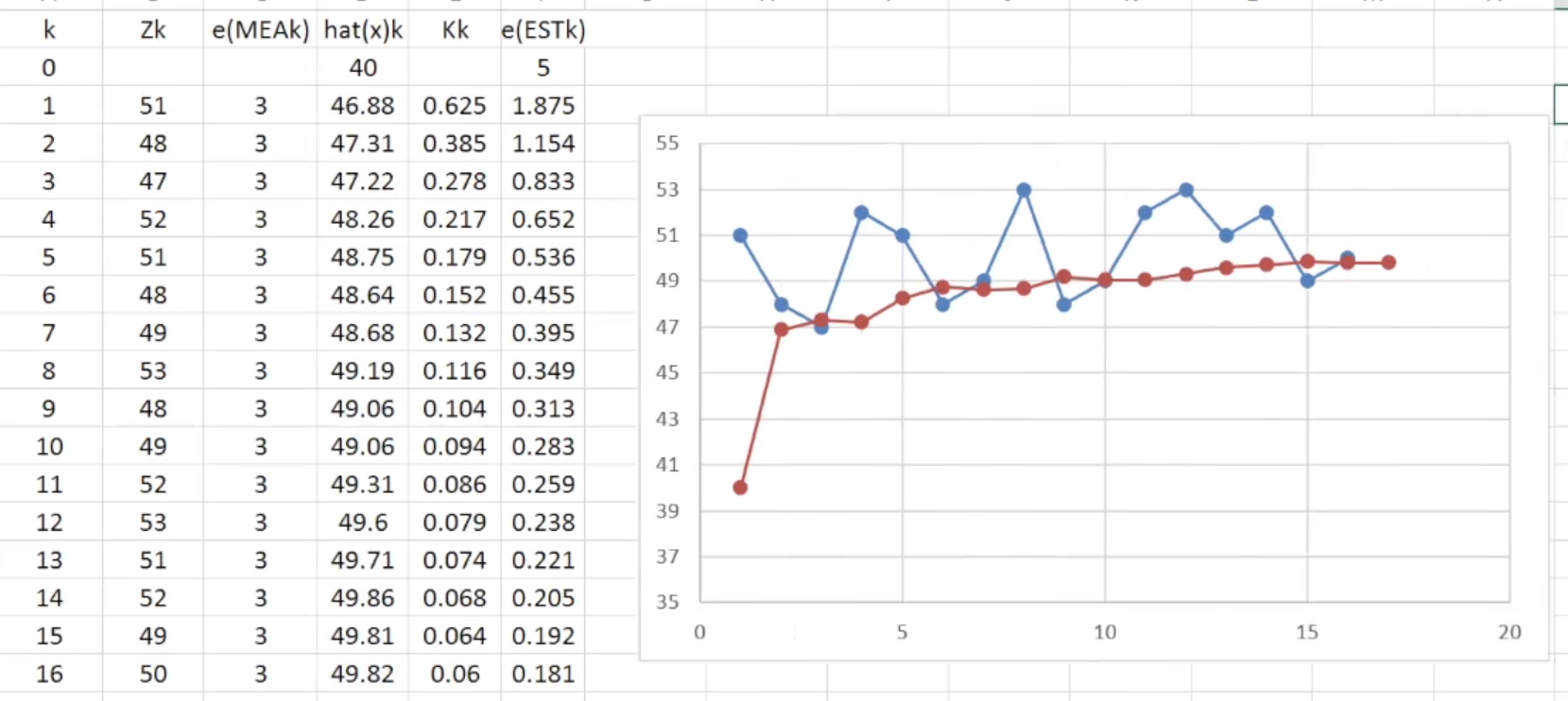
可以看到,随着测量次数的增加,最后一次测量结果会变得越来越不重要,也就是说k越大,新的估计值越接近上一次的估计值,反之则接近这一次的测量值,k反应了这两个数据的重要程度。把其中的$\frac{1}{k}$表示成一个系数后:

其中的$k_k$就是卡尔曼增益/因数,这次的估计值只和上一次的估计值和这一次的测量值有关,这是一种递归算法,不需要追溯很久以前的数据。

关于卡尔曼增益的公式是卡尔曼滤波器的核心公式。它和上一次的估计误差,以及这一次的测量误差有关,当上一次的估计误差较大,则$k_k$趋近于1,这一次的估计值会越接近这一次的测量值。当这一次的测量误差较大,$k_k$趋近于0,这一次的估计值会趋近于上一次的估计值。
因此解决问题步骤如下(相关公式推导会在后面章节给出):
计算$Kalman Gain $:
$$
k_k = \frac{e_{EST_{k-1}}}{e_{EST_{k-1}} + e_{MEA_k}}
$$计算这一次的估计值:
$$
\hat{x_k} = \hat{x_{k-1}} + k_k(z_k - \hat{x_{k-1}})
$$更新这一次的估计误差:
$$
e_{EST_{k}} = (1-k_k)e_{EST_{k-1}}
$$

在不断地递归计算中,可以得出越来越接近真实值的结果。
数学基础
数据融合(Data Fus’ion)


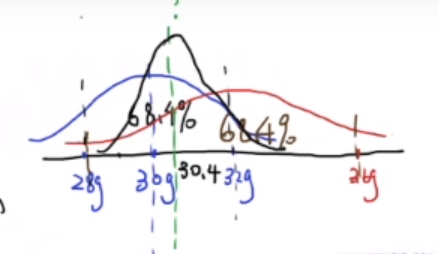
根据两个称的结果,我们对真实数据进行了预测,这个预测是30.4g,并且在数学上证明了这是最优解。这种把数按一定权重融合在一起进行预测的方法就是数据融合。融合后的图形具有更小的标准差,预测更准确。
协方差矩阵(Covarince Matrix)
$$
cov(X,Y) = \frac{\sum_{i=1}^n (Xi-\bar{X})(Y_i - \bar{Y})}{n-1}
$$
协方差的意义:如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义)。如果结果为负值, 就说明两者是负相关。如果为0,则两者之间没有关系,就是统计上说的“相互独立”。
协方差矩阵把方差、协方差在一个矩阵中表现出来,它表现了变量之间的联动关系。
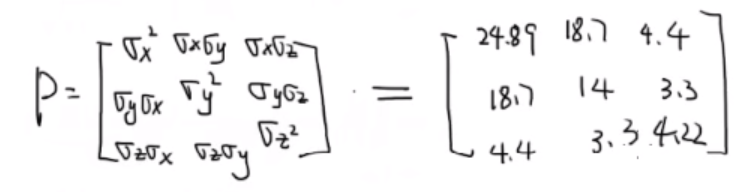
通过矩阵运算计算协方差:
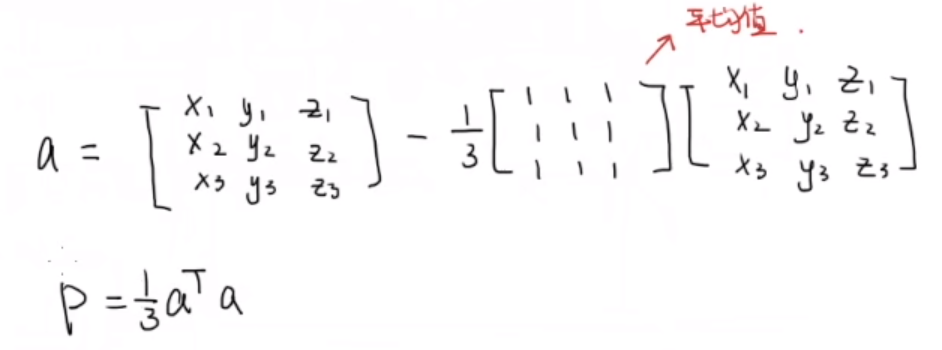
举例:
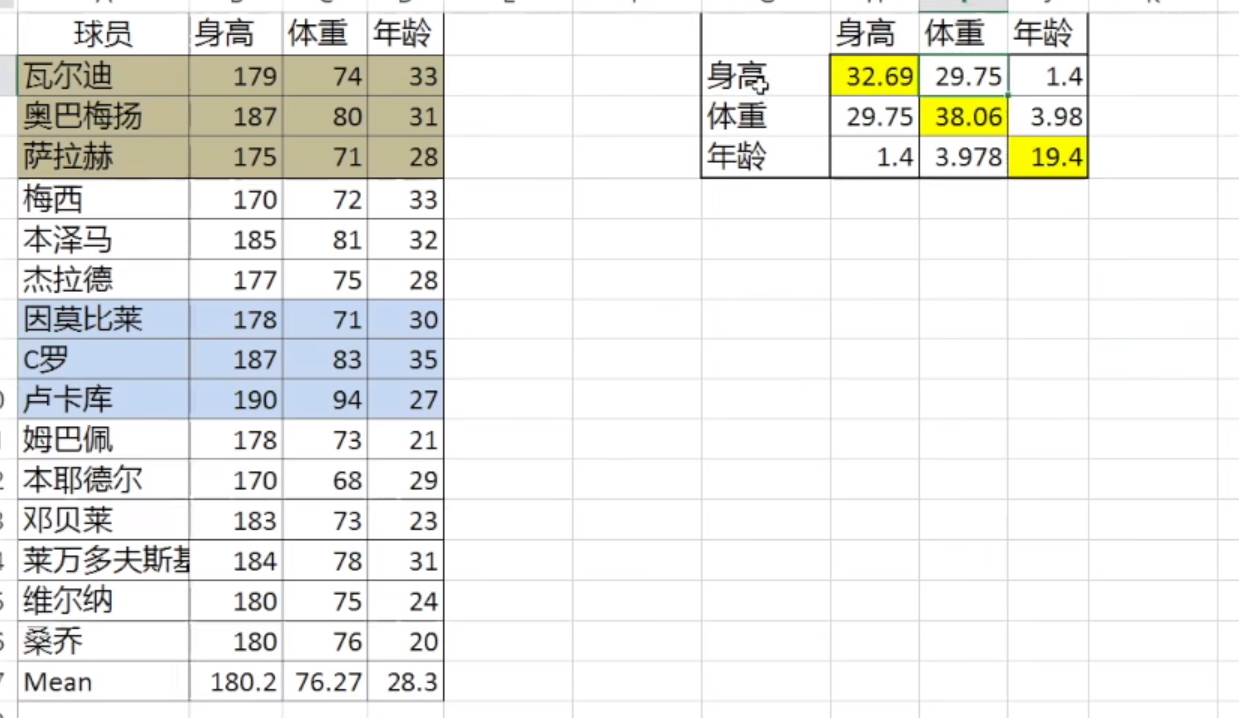
可以看出球员身高、体重、年龄的方差都较大,说明职业球员和这三方面的关系不大。体重和身高的协方差较大,说明体重和身高的相关性较大。年龄和体重、身高的协方差较小,说明虽然它们正相关,但相关性较小。
状态空间表达(State Space Representation)
具体内容可查看《现代控制理论精讲》的内容。


世界因为充满了不确定性,我们的模型不准确,就需要在状态空间方程后面加上一项,前面的模型加上过程噪音(Process Noise),后面有用测量误差,需要加上测量噪音(Measurement Noise)。在这两个不确定的情况下,如何去估计一个精确的$\hat{x}$,这就是卡尔曼滤波器要解决的问题。
卡尔曼增益详细数学推导
首先记住方差和期望的公式:
$$
D(X) = E[(X-E(x))^2] = E[X^2-2XE(X)+[E(x)]^2] = E(X^2)-[E(x)]^2
$$
同理,协方差:
$$
cov(X,Y) = E[(X-E(X))(Y-E(Y))] = E(XY) - E(X)E(Y)
$$
在上一章中,我们发现因为不确定性系统附有过程噪音$w_{k-1}$和测量噪音$v_{k}$。
$$
x_k = Ax_{k-1} + Bu_{k-1}+ w_{k-1}
$$
$$
z_k = Hx_k + v_k
$$
过程噪声和测量噪声都是不可测的,但是我们可以假设它符合正态分布。因此它的概率分布符合$P(w)~(0,Q)$,其中0代表期望,Q是协方差矩阵,求法:
$$
Q = E[w w^T] = E[\begin{matrix} w_1^2 & w_1w_2 \ w_2w_1 & w_2^2 \end{matrix}] =[\begin{matrix} E(w_1^2) & E(w_1w_2) \ E(w_2w_1) & E(w_2^2) \end{matrix}] = [\begin{matrix} \sigma_{w1}^2 & \sigma_{w1}\sigma_{w2} \ \sigma_{w2}\sigma_{w1} & \sigma_{w2}^2 \end{matrix}]
$$
注意里面的$\sigma_{w1}\sigma_{w2}$不是两个标准差相乘,而是协方差。$v_k$的协方差矩阵为R,算法同上。
由于噪音是没办法建模的,我们只能去掉噪音计算直接计算(像往常一样),得出来的值称为先验估计值$\hat{x_k^-} $:
$$
\hat{x_k^-} = A\hat{x_{k-1}} + Bu_{k-1}
$$
$$
\hat{x_{kmea}} = H^{-1} z_k
$$
这样$x_k$存在两个结果,一个是算出来的,一个是测出来的。这两个结果都是不准确的,因此卡尔曼滤波器的任务是从这两个不太准确的结果,来得出一个更加准确的结果。这里称为后验估计值$\hat{x_k}$:
$$
\hat{x_k} = \hat{x_k^-} + G(H^{-1} z_k - \hat{x_k^-})
$$
G是0到1的一个数,这个数决定了估计值是偏向于算出来的结果还是测出来的结果。教科书上令$G=k_kH$,则有:
$$
\hat{x_k} = \hat{x_k^-} + k_k( z_k - H\hat{x_k^-})
$$
这里$k_k = GH^{-1}$的取值范围是[0,$H^{-1}$],这是一个矩阵。同样当这个数趋近0时更相信算出来的结果,当趋向$H^{-1}$时更相信测出来的结果。
目标:选择一个合适的$k_k$,使得新的估计值趋向于实际值。
为了量化误差,引入$e_k$,同样它符合正态分布$p(e_k)~(0,P)$:
$$
e_k = x_k - \hat{x_k}
$$
$$
P = E[e e^T] = E[(x_k - \hat{x_k})(x_k - \hat{x_k})^T] = [\begin{matrix} \sigma_{e1}^2 & \sigma_{e1}\sigma_{e2} \ \sigma_{e2}\sigma_{e1} & \sigma_{e2}^2 \end{matrix}]
$$
为了使得估计值和实际值的差距最小,必须使得数值的方差最小。因此我们目标是选取合适的$k_k$使得这个P矩阵的迹$tr(P)$最小,方差就是最小的。
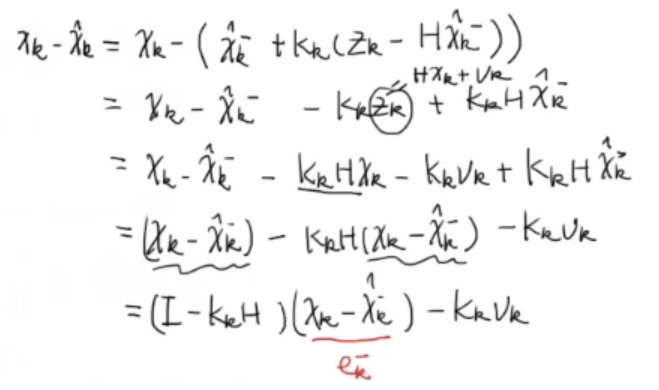
计算出来$x_k - \hat{x_k}$代入原式:
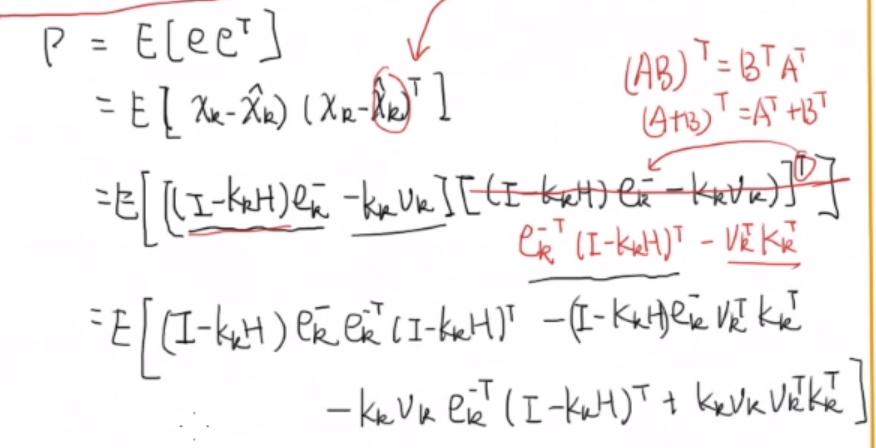
之后是分布求每个部分的期望:

然后开始计算迹$tr(P)$:

在对迹进行矩阵求导时,我们需要储备线性代数矩阵求导的知识:
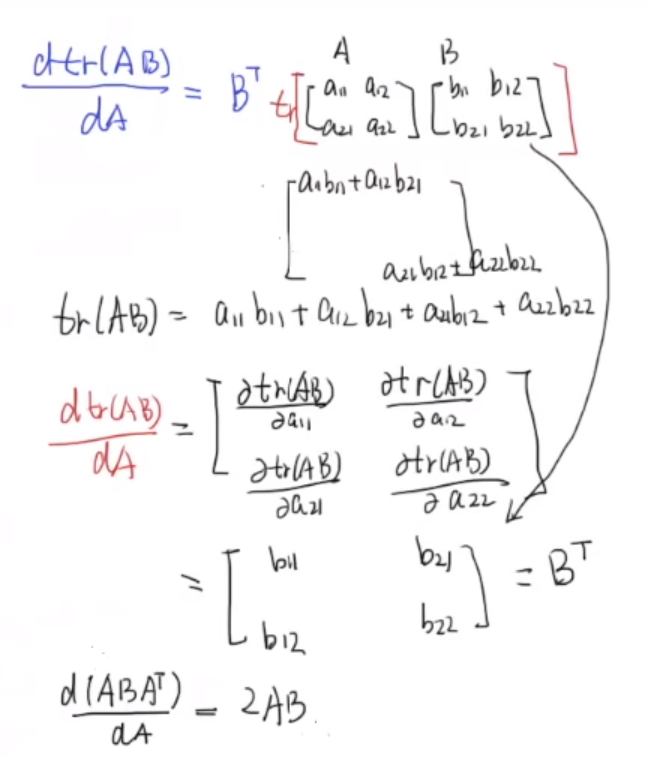
然后求极值点,迹对矩阵求导:

最后得出结论:
$$
k_k = \frac{P_k^- H^T}{HP_k^-H^T + R}
$$
其中$P_k^-$是$e_k^-$的协方差矩阵,R是噪声矩阵的协方差矩阵,H是测量矩阵。
当R越大时,说明噪声方差特别大,因此$k_k$会趋近于0,估计值趋近计算值。当R特别小时,$k_k$趋近于$H_{-1}$,估计值趋近于测量值。
误差协方差矩阵数学推导_卡尔曼滤波器的五个公式
复习:
原系统:
$$
x_k = Ax_{k-1} + Bu_{k-1} + w_{k-1}
$$
$$
z_k = Hx_k + v_k
$$
其中w~P(0,Q),v~P(0,R)
先验估计:
$$
\hat{x_k^-} = A\hat{x_{k-1}} + Bu_{k-1}
$$
后验估计:
$$
\hat{x_k} = \hat{x_k^-} + k_k( z_k - H\hat{x_k^-})
$$
卡尔曼增益:
$$
k_k = \frac{P_k^- H^T}{HP_k^-H^T + R}
$$
上一章中,误差的协方差矩阵是我们还没有找出来的。
$$
e_k^- = x_k - \hat{x_k^-} = A{x_{k-1}} + Bu_{k-1} + w_{k-1} - A\hat{x_{k-1}} - Bu_{k-1} = Ae_{k-1} + w_{k-1}
$$
$$
P_k^- = E[e_k^- (e_k^-)^T]
$$

因此得出公式:
$$
P_k^- = AP_{k-1} A^T + Q
$$

自此,卡尔曼滤波器的五个公式全部推导出来了。它分为预测和校正两个阶段,一开始要给x和P赋予一个初值,然后进行预测。通过预测得出x和P的先验值,通过这两个先验值可以进入校正阶段,求出卡尔曼增益和x的后验估计。最后还要更新一下误差协方差P。通过不断重复这两个阶段,x会逐渐趋近真实值。
直观理解和二维实例

在这个例子中,我们建立了一个人走路时关于位置和速度的数学模型,并且用卫星测量它。由于模型和测量的不准确性,存在一定的过程噪声,所以需要用到卡尔曼滤波器。
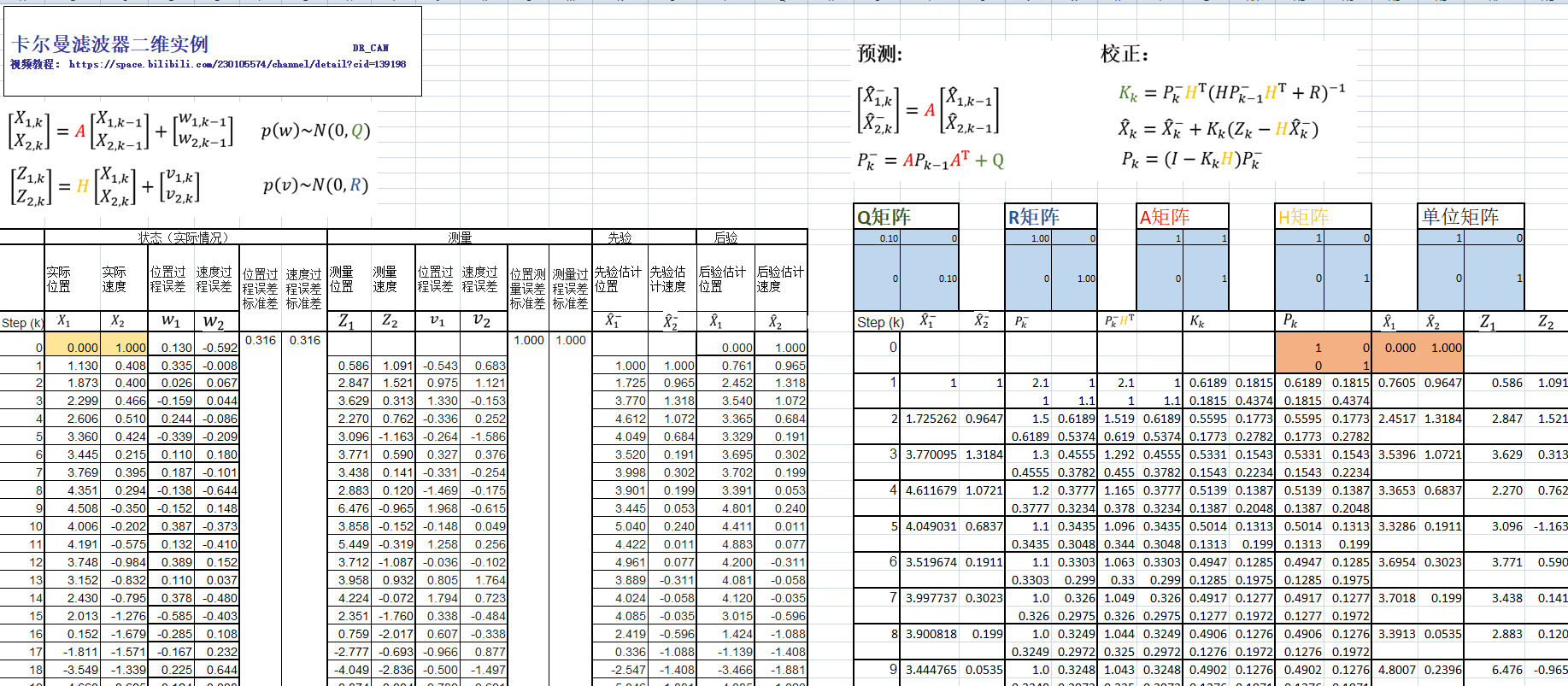
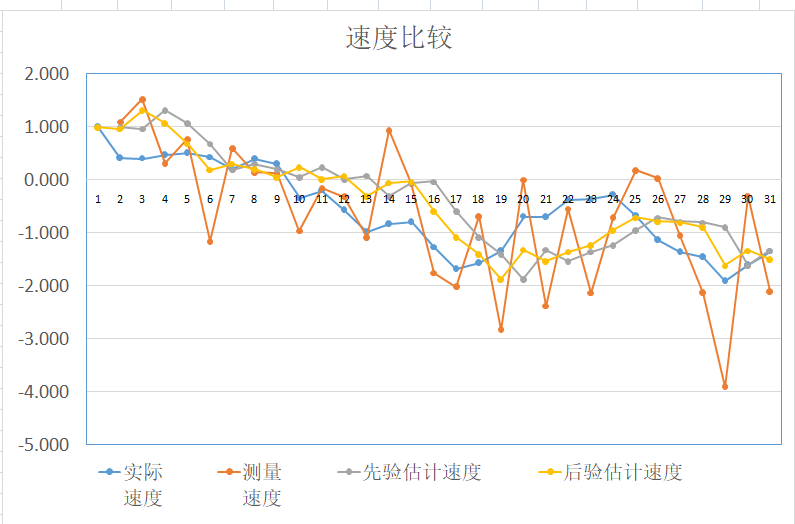
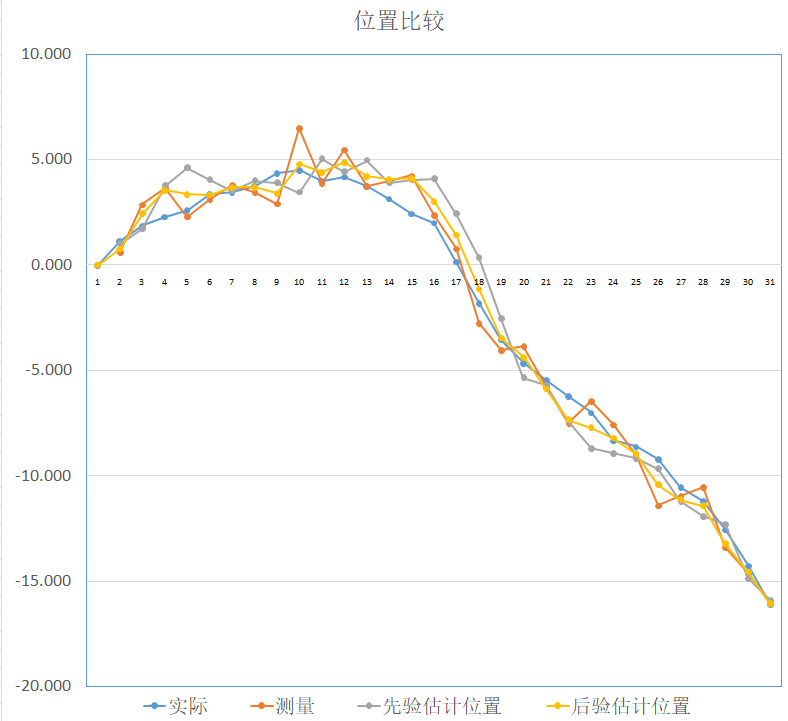
可以看到,每一步的测量值和先验估计值通过卡尔曼滤波器之后,都可以得到一个更加准确的后验估计值。
卡尔曼滤波器是最优化的线性滤波器,用在线性系统中可以得到最优估计值。
扩展卡尔曼滤波器(Extended Kalman Filter)
任务:将非线性系统线性化,然后才能使用卡尔曼滤波器。



这部分的理解待完善。。。



