参考视频:非线性控制理论
Lyapunov直接方法

以上就是正定,半正定,负定,半负定的定义。

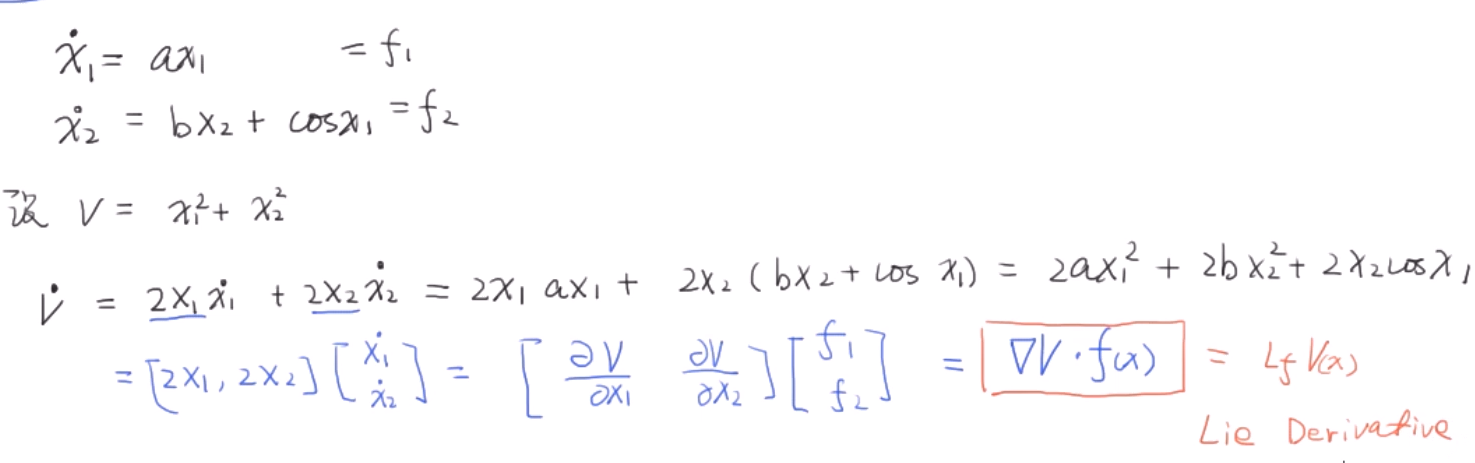
例子(钟摆):
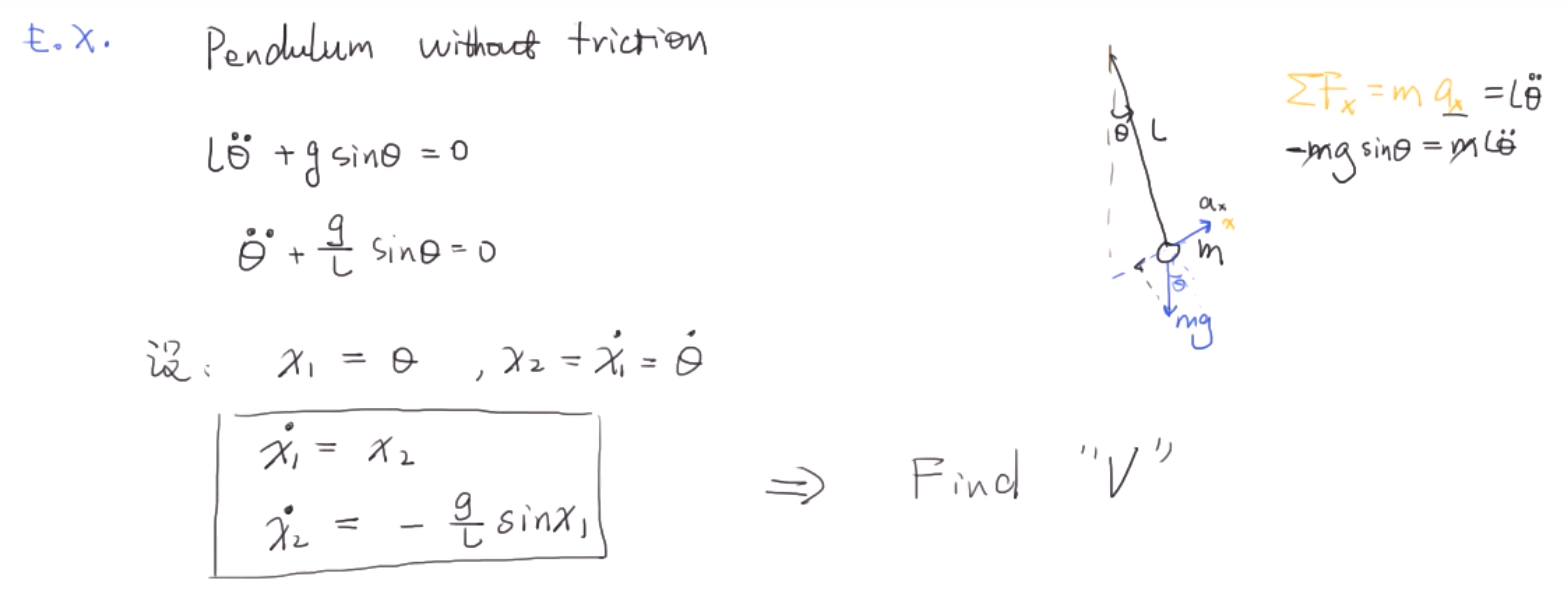
对于一个非线性系统,一般来说没有固定的方法找V,但可以从能量入手。

这里说明了$x_1$,$x_2$有界,但不代表$x_1$,$x_2$会随着时间趋向于0,这里李雅普诺夫函数设计的是它的能量,那么$\dot{V}$是能量随时间的变化,它等于0。系统符合能量守恒,自然是稳定的。
在有摩擦力的情况下:

当$x_1$取任意值,$x_2=0$时,$\dot{V} = 0$。这时系统是半负定的,系统稳定,但在这里没有在数学上得出渐进稳定的结论。
不变性原理(The Invariance Principle-LaSalle’s Theorem)
因此我们要引入一个新理论来扩大李雅普诺夫稳定性的判定。
当满足下列三点要求,系统渐进稳定:
- $V(x)$在区域D正定。
- $\dot{V} (x)$在一个区域$R \in D$内半负定。
- $\dot{V} (x)$在R中的任何轨迹不等于0,除了x =0。
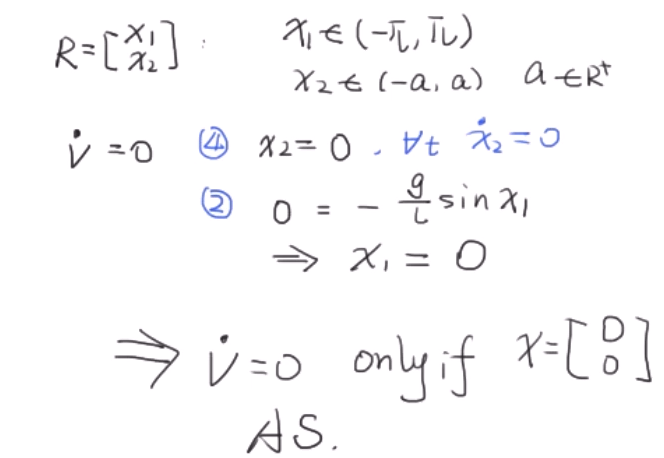
因此满足以上三个条件,系统渐进稳定。
另外的例子:

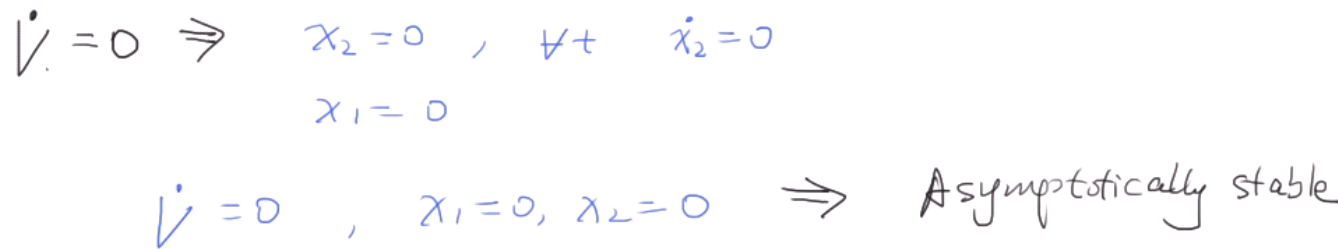
非线性系统稳定性设计
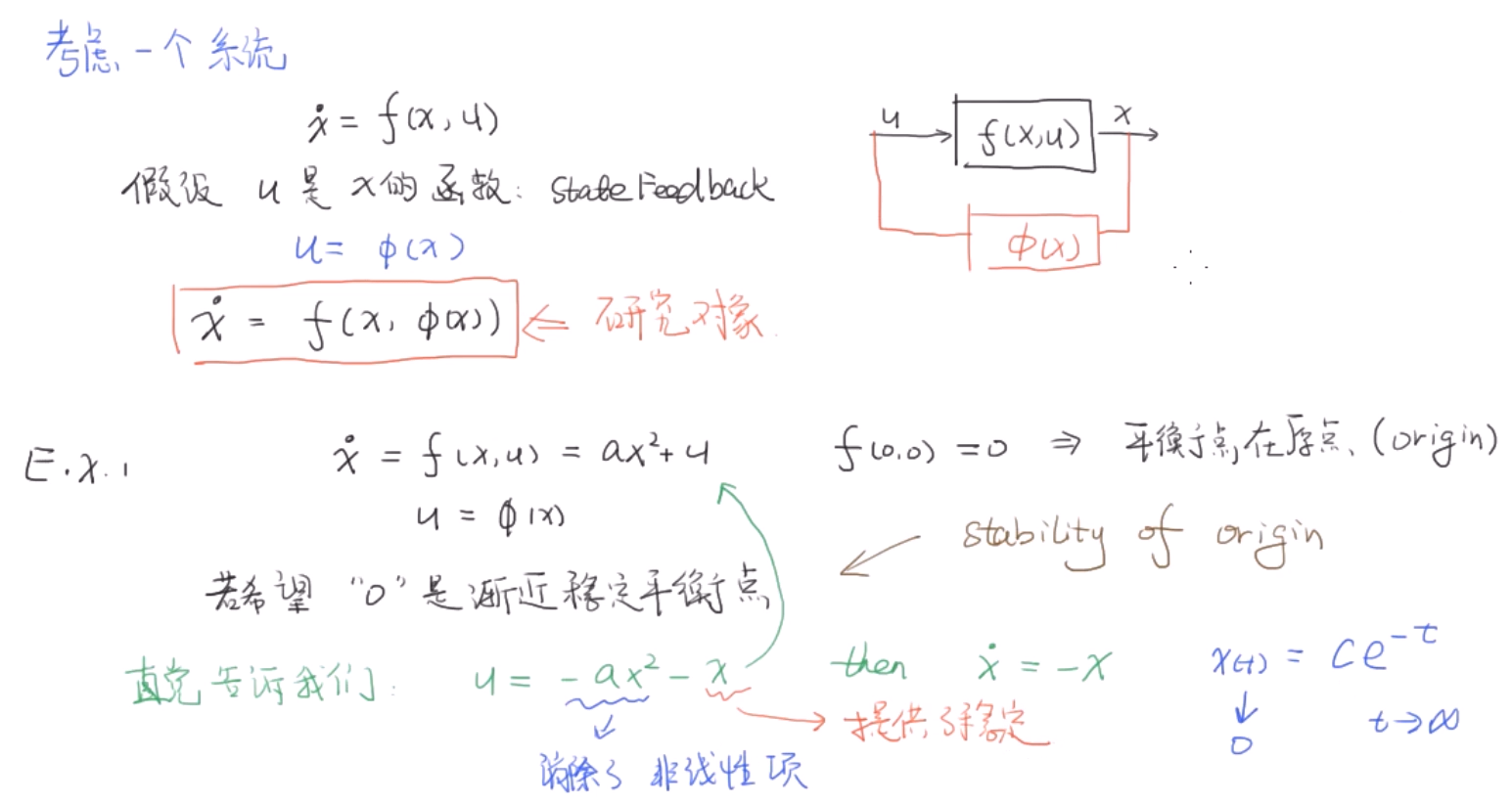
这个方法中a必须知道,而且方法很直接简单粗暴地把非线性的部分抵消掉,但不一定最佳,这种方法叫做反馈系统线性化$(Feedback Linerization)$。
代替方法是李雅普诺夫的直接方法:

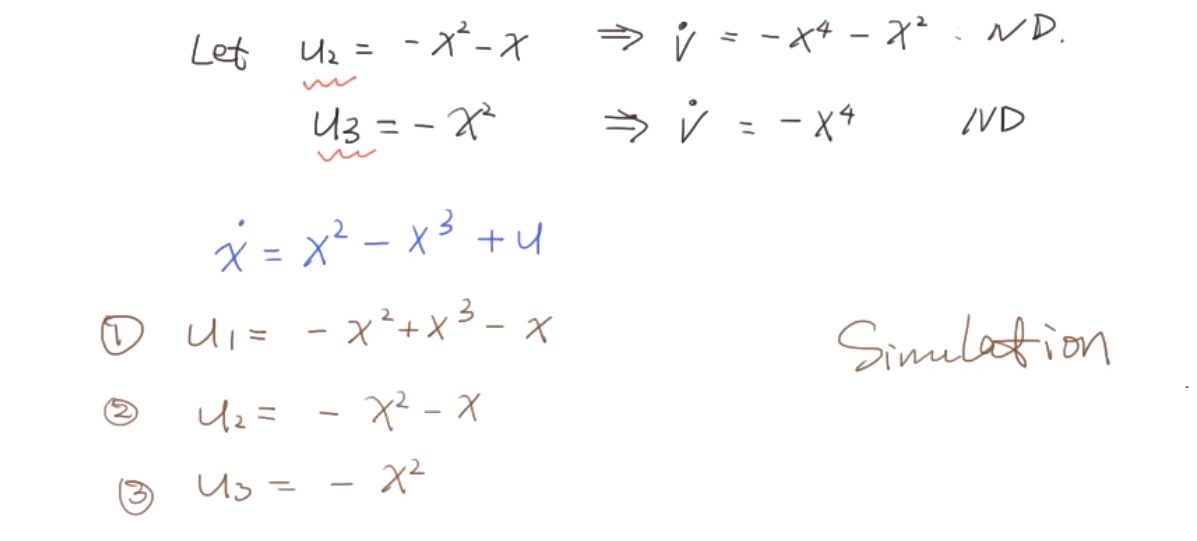
这里又设计出两种方案,对这三种方案进行仿真看运行效果。
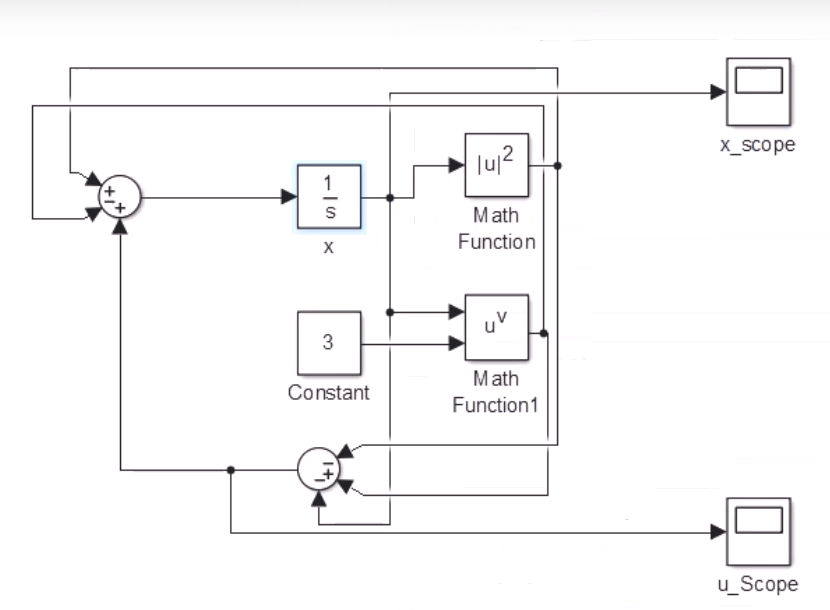
第一种方案虽然可以稳定,但是u初始值过大,这就是为什么要避免简单粗暴地方式设计控制器。所以才有了下面两项的替代。

其中$u_1$是黄线,$u_2$是粉线,$u_3$是蓝线,$u_3$输出衰减非常慢,很长时间才会趋近于0,这是由于
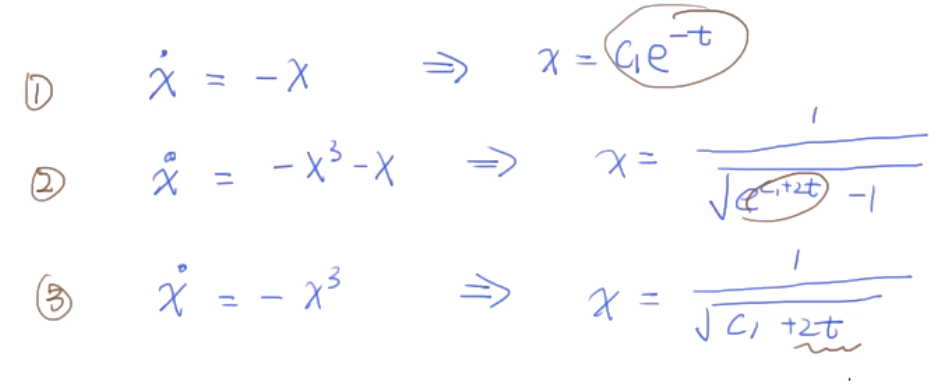
前面两项由于是指数变化,收敛速度快很多。
非线性反步控制(Nonlinear Backstepping Control)(重要)
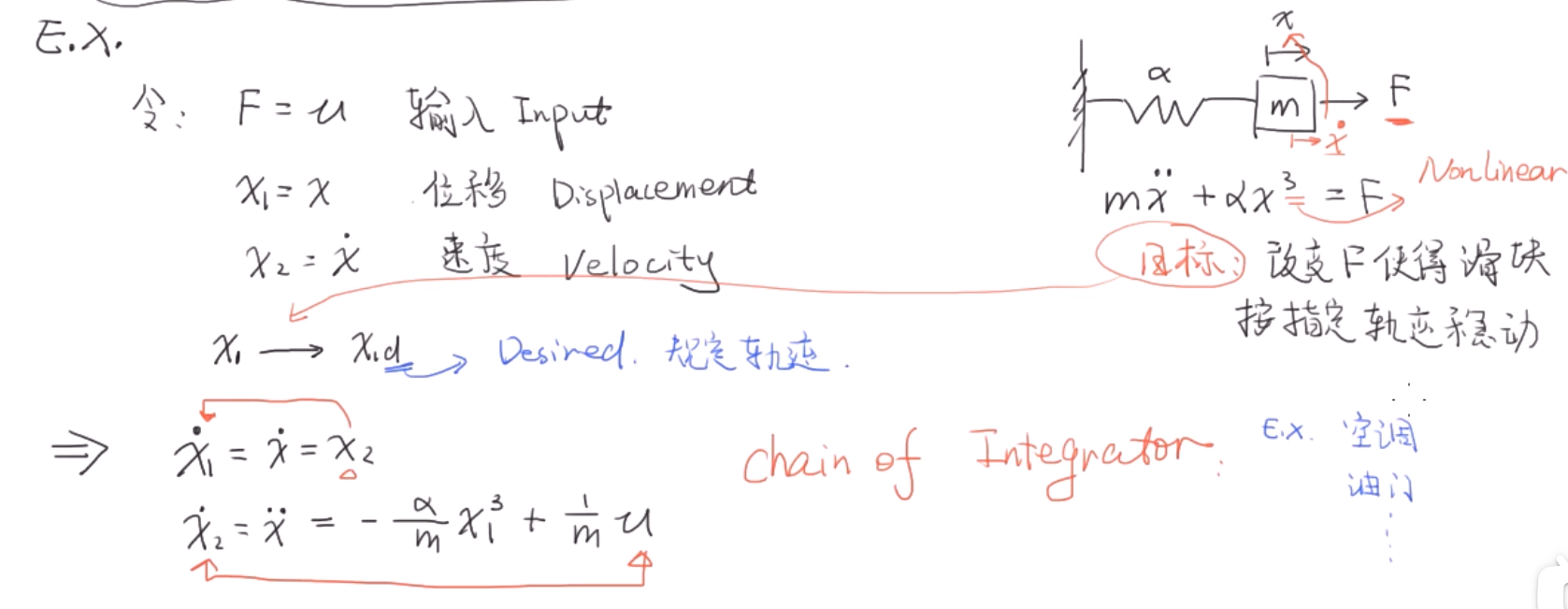
这是一个链式控制,力改变物体运动的速度,速度又会导致物体位置上的改变。

为了控制小车沿着指定轨迹行走,需要引入e,并设置控制器使得e最终趋向于0,那么李雅普诺夫函数需要设置为e的函数。要使$\dot{V}_1$满足渐进稳定的条件,可以求得$x_2$的期望值。

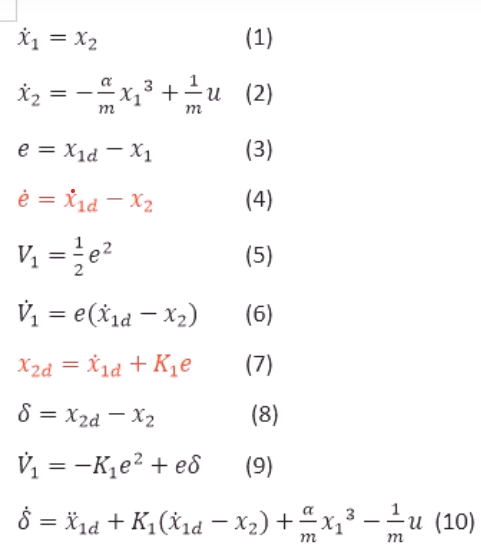
我们的新目标是让$x_2$的期望值尽量趋近$x_2$,又需要引入误差$\delta$,目的使其趋向于0,在回代之后,把e去掉。然后建立新的李雅普诺夫函数。这个函数可以保证$\delta$和e都趋近于0。
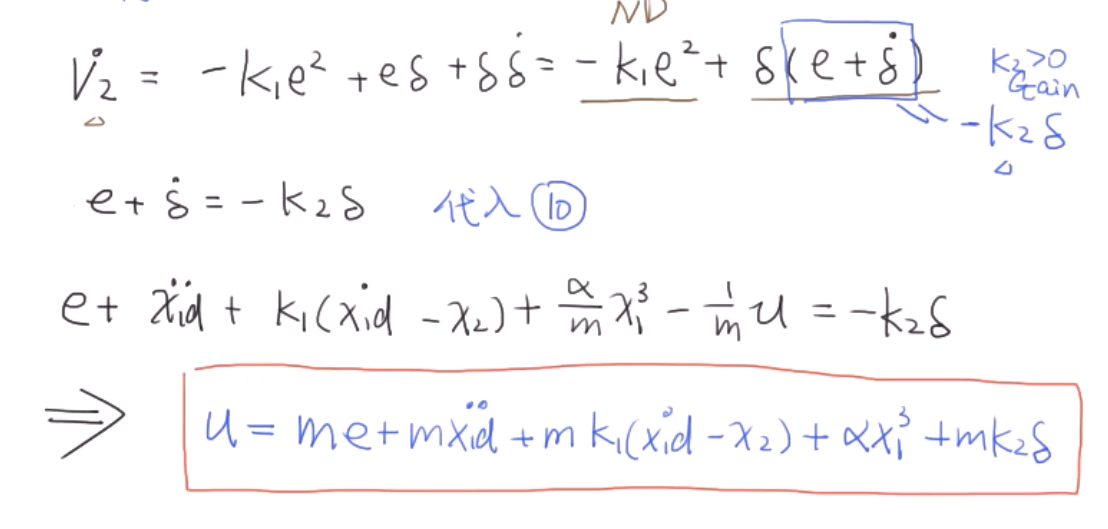
构建新的李雅普诺夫函数之后,利用渐进稳定原则,可以设出$\dot{V}_2$的形式,从而求得u的解。
验证:
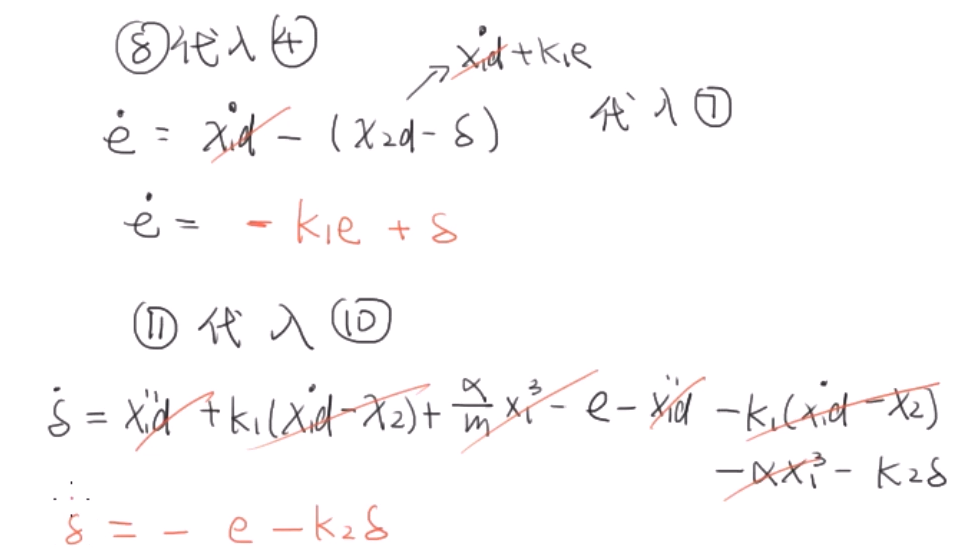

这就是通过反馈系统线性化。最后得到的是一个线性系统。
仿真:
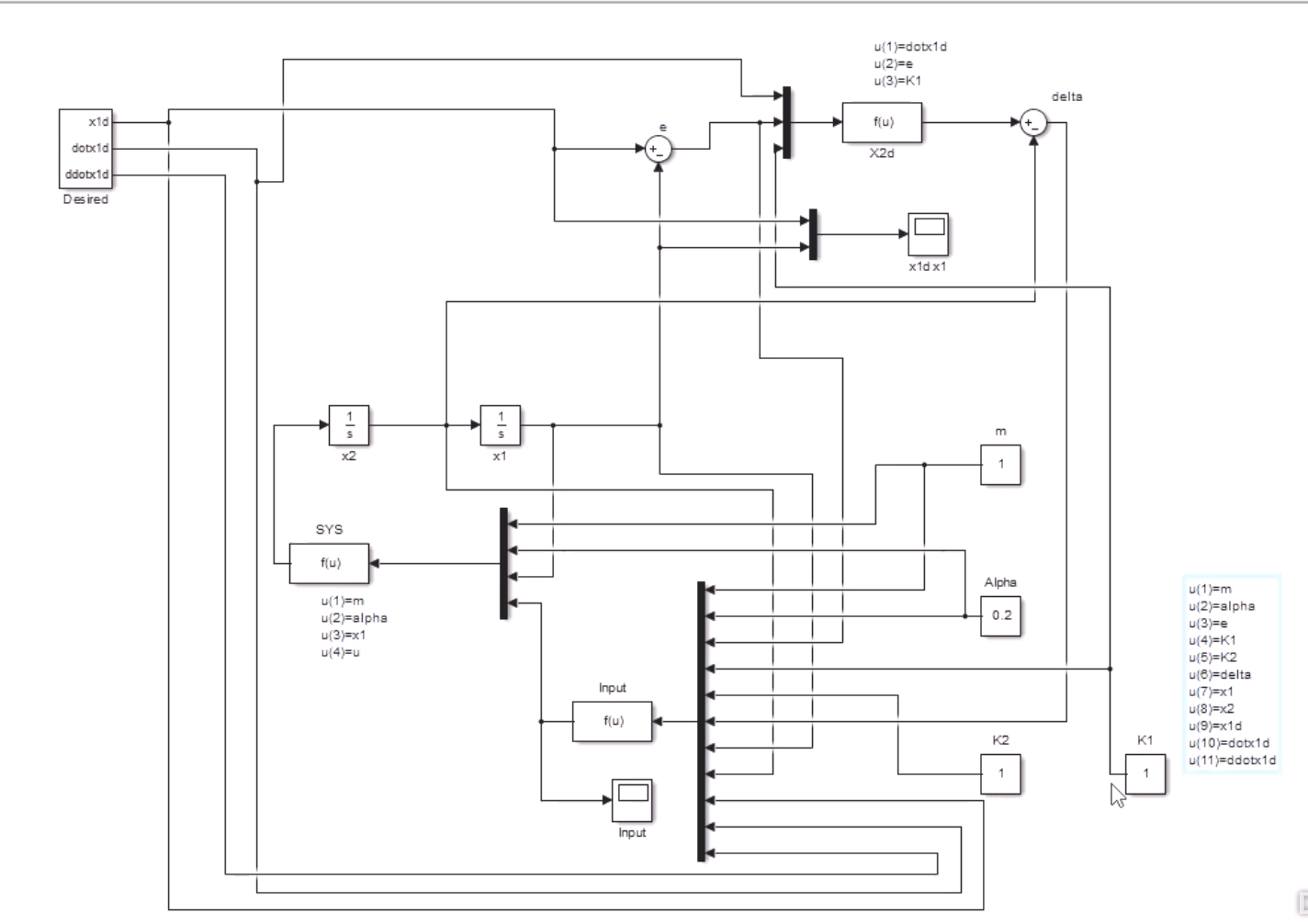
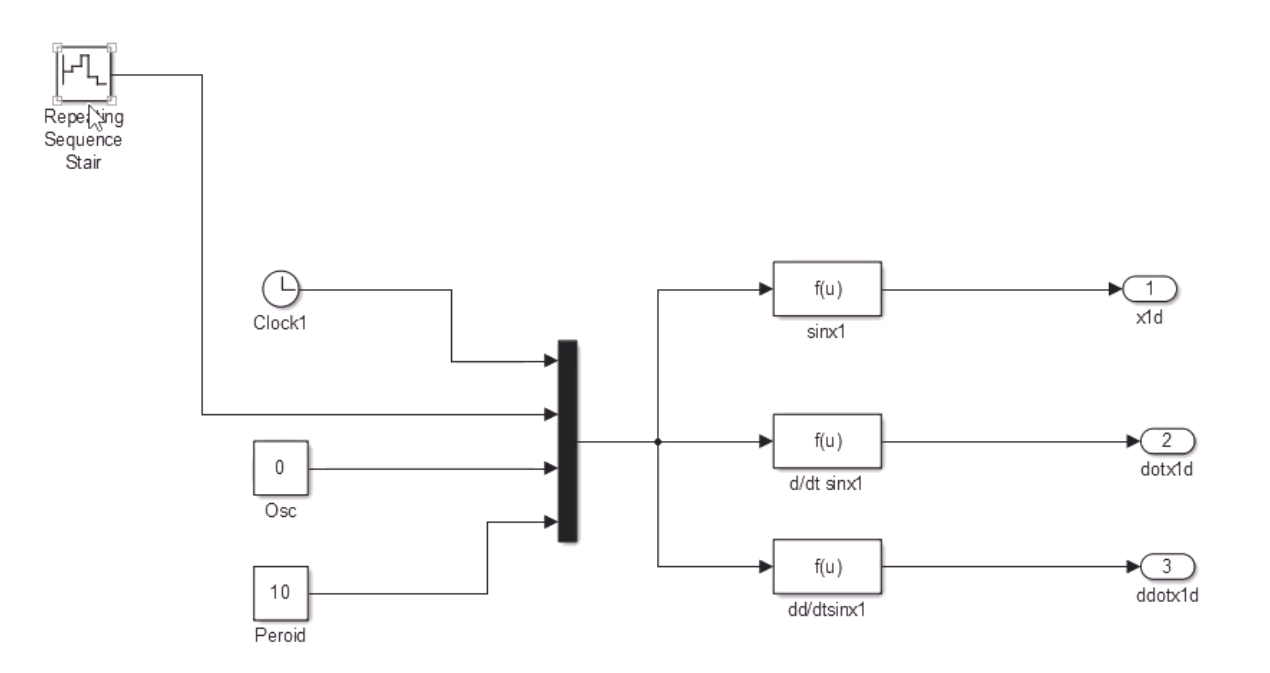

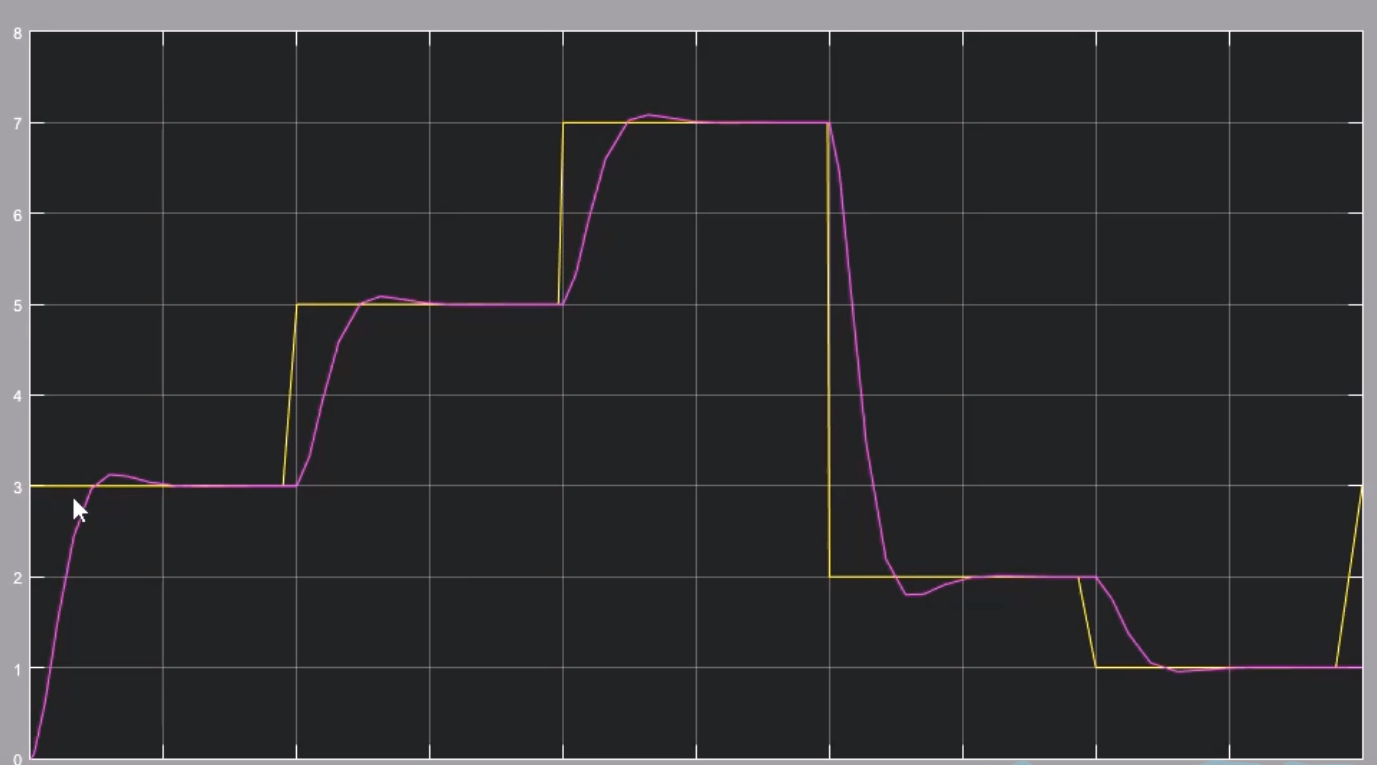
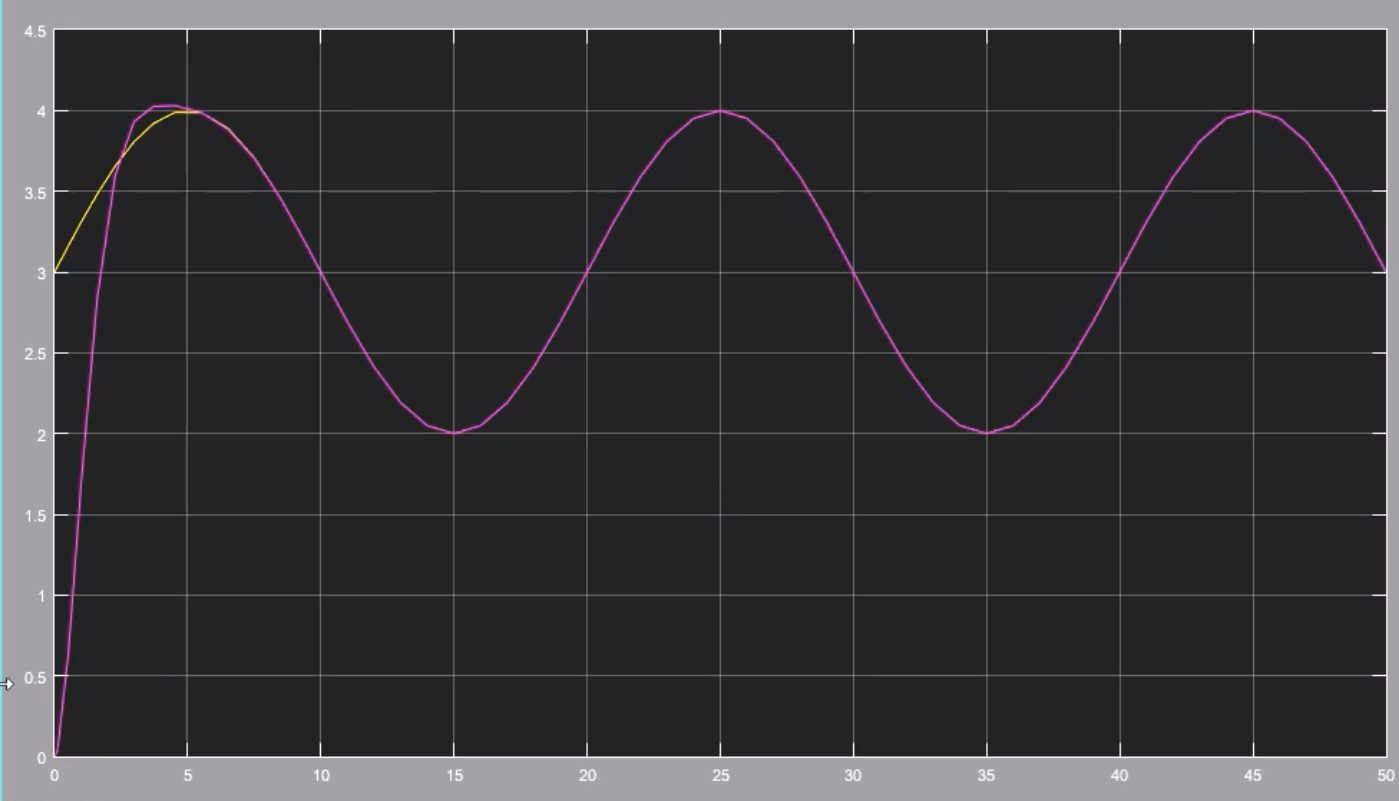
总结
首先,设计系统的目标是轨迹跟踪,让$x_1$跟随设定的$x_{1d}$。而通过u可以作用到$x_2$,通过$x_2$又可以控制$x_1$,这是一个控制链。因此设计控制器需要两步:第一步是通过让$x_1$趋近 $x_{1d}$来设计$x_{2d}$,这个可以理解为中间输入。第二步是通过让$x_2$趋近$x_{2d}$来设计u。

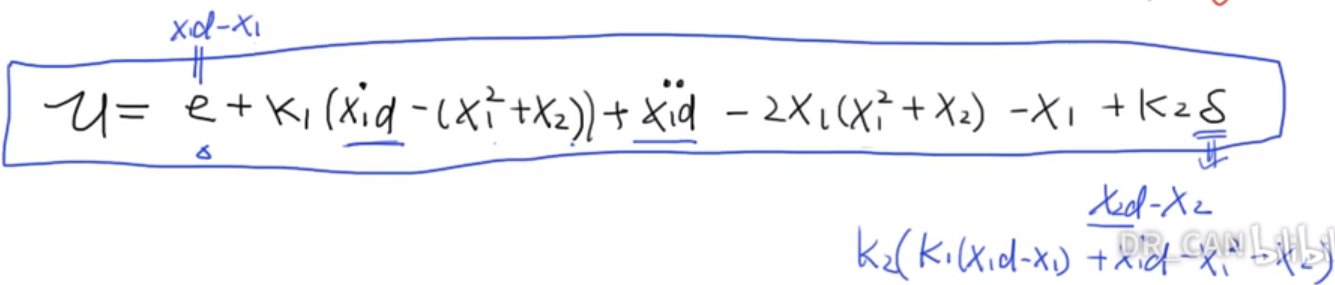
非线性自适应控制器(Nonlinear Adaptive Controller)

这个就是只有一层的反馈控制,用的是之前的反步控制法。前提是参数a必须已知,那么如果a不是已知怎么办?

由于参数a未知,我们可以设一个预设a。

然后再根据李雅普诺夫直接方法,并采用Lyapunov-like引理把公式中未证明的e趋近于0给证明出来,把a的解出来的预设值代入u中,就可以得到输入了。
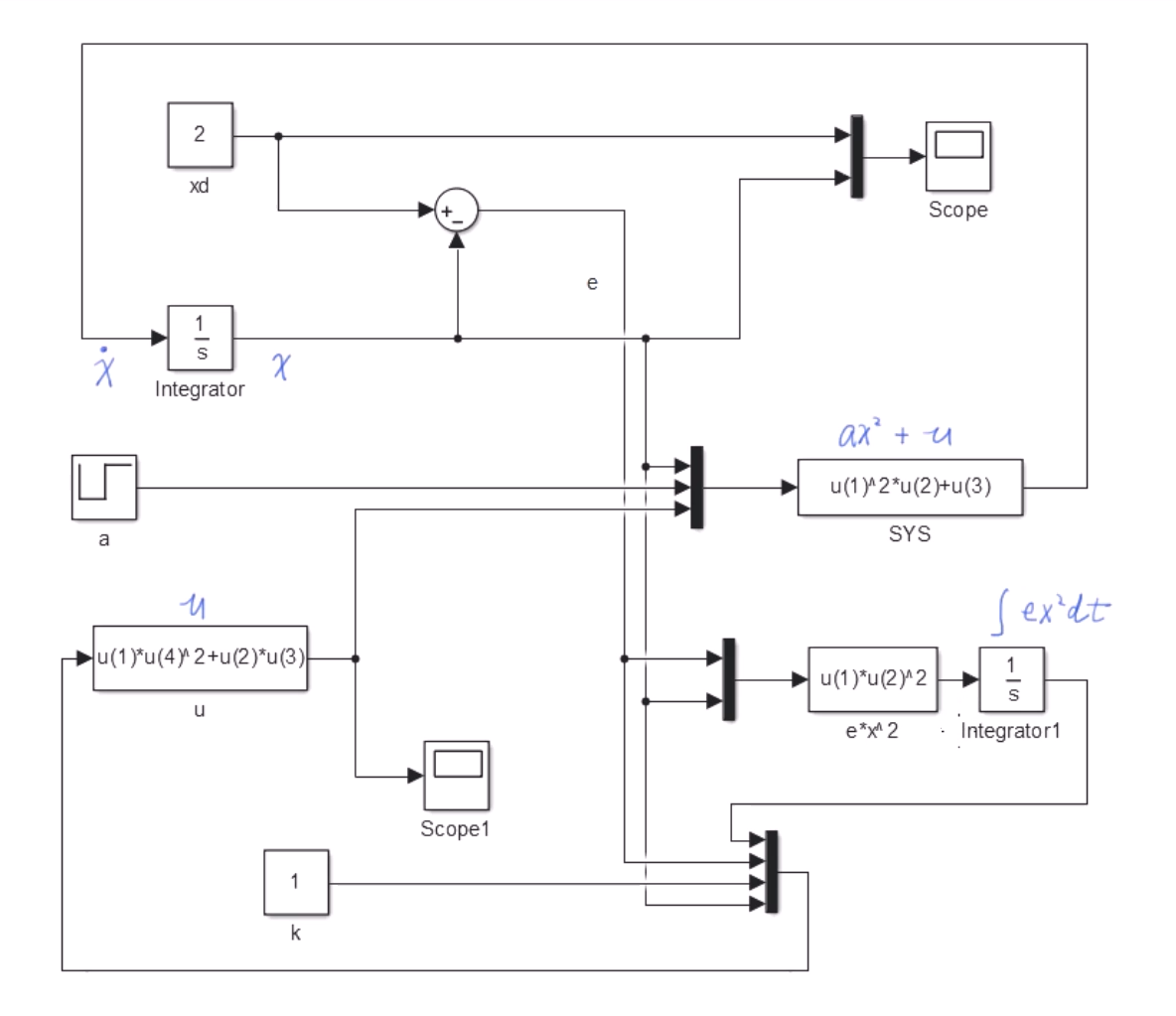
这就是自适应控制,无论a怎么变,系统都能够很好地跟随预设值的变化。使得预设的a在一定程度上跟上实际的a,并使e趋近于0。
练习:如果上一章的第一个系统的参数α未知,如何进行自适应控制?
总结:按照反步法先设计一个控制器。设计好后,控制器中参数有未知项。然后再设计一个Lyapunov函数,求导,并把设计好的控制器(输入的未知量要替换成估计值,控制器中的e是实际值)代入其中,来求未知参数的估计值,通过不断调整估计值来使误差收敛。根据Barbalats lemma判定Lyapunov函数中除未知量以外的其他变量,都会在t趋近于无穷时收敛到0,从而得出改估计值以及控制器可以使系统渐近稳定,也就完成了基于反步法的自适应控制器设计。
非线性鲁棒控制器(Robust Controller)_滑模控制(Sliding Mode)
鲁棒控制器会存在有界的误差(例如:空调系统、巡航系统)。
在鲁棒控制中,上一章变化的a值会更加苛刻,它并不是常数,而是一个变化的有界量。

这里设了一个$\rho (x)>|f(x)|$,然后设出一个u,可以得出系统稳定。
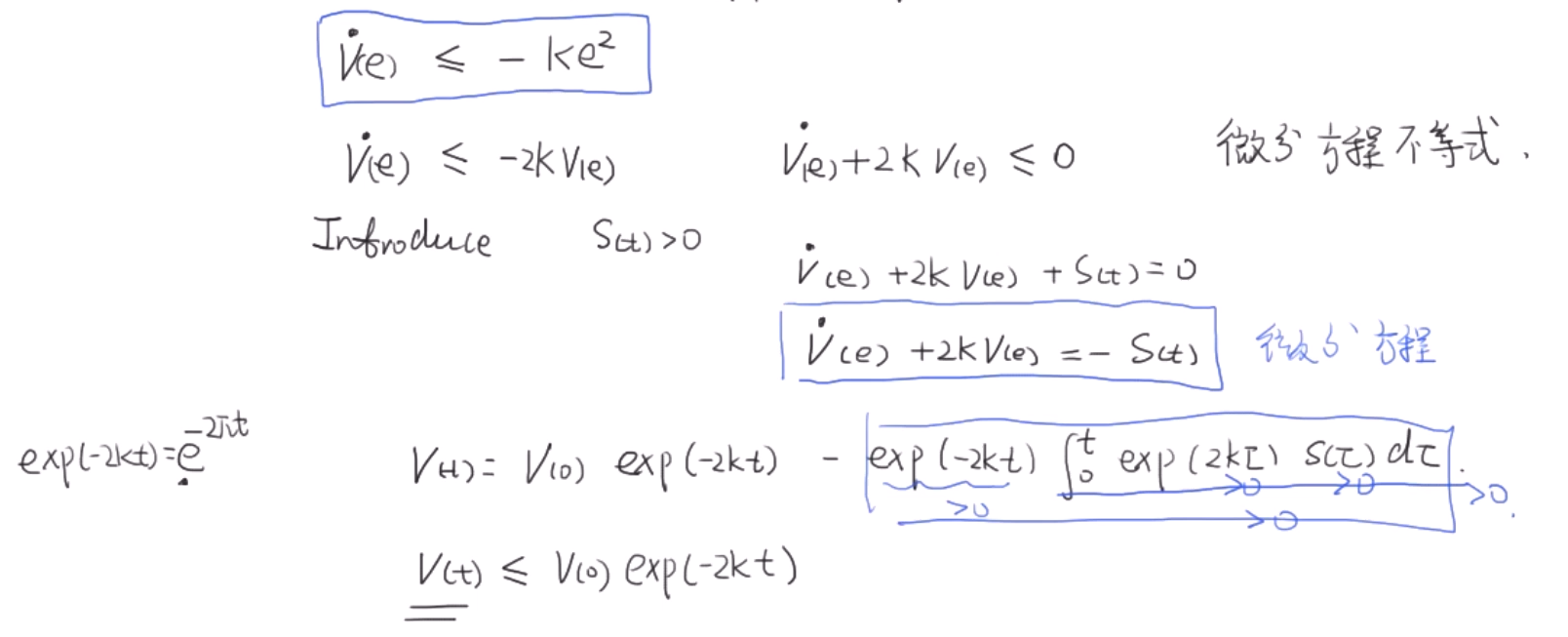
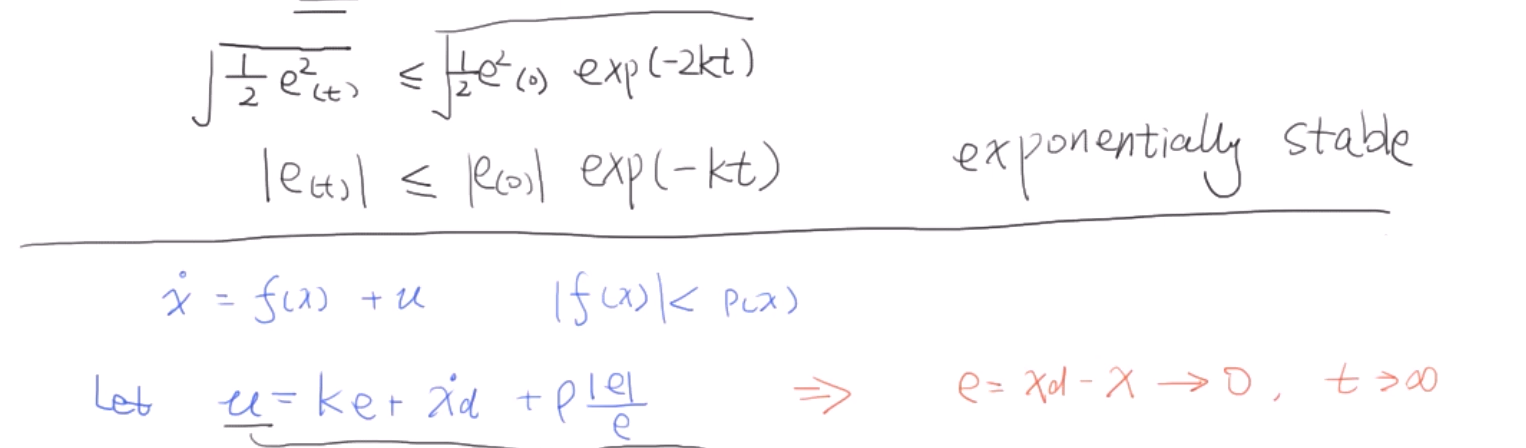
然后引入松弛变量$S(t)$,可以解出$V(t)$的最大值,从而解出$e(0)$的最大值是一个随着时间指数衰减的函数,也就证明了渐进稳定。这种u的设法是可行的。

这里用相平面分析,如果不看后面两项,相平面上的曲线是一条过原点单调递减的直线。最后一项用来抵消第二项,容易证明e小于0时,e的导数一定大于0,e大于0时,e的导数一定小于0,因此0是e唯一的稳定点。这就是滑模控制(Sliding Mode)。可以看到这种控制不需要知道$f(x)$中确切的参数值,只需知道它的上界即可,满足鲁棒控制的要求。
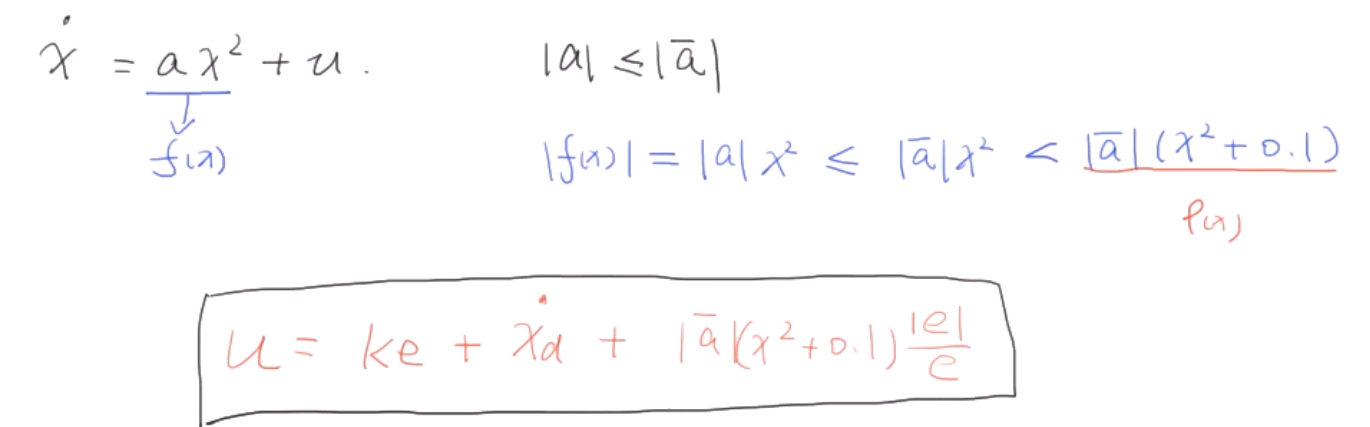
设计控制器u时只需要找到一个恒大于$f(x)$的函数即可。
非线性鲁棒控制器(Robust Controller)_高增益和高频控制器(High Gain and High Frequency Controller)

通过设置辅助的$u_{aux}$控制器,可以达到很好的控制效果,上一章令
$$
u_{aux}=\rho \frac{e}{|e|}
$$
这是滑膜控制,它的缺点是u的变化幅度过大,会给执行器带来很大的挑战。接下来介绍两种新的辅助控制器:
$$
u_{aux2}= \frac{1}{\epsilon} \rho^2 e ,\epsilon>0
$$
这就是High Gain,用足够大的输入抵消不确定性。
$$
u_{aux3}= \frac{\rho^2 e}{\rho|e| + \epsilon},\epsilon>0
$$
这里当$\epsilon=0$时是Silding Mode。当$\epsilon \neq 0$时,$|u_{aux3}| < \rho$,和滑膜控制相比,切换不再那么剧烈,更加平缓一些。




以上就是第二种鲁棒控制器的证明,最后可以看到稳态误差不是一个趋近于0的结果,但误差会小于一个值,当$\epsilon$取值较小可以有效减小稳态误差,但是会给执行机构u带来很大的负担,需要权衡。第三种鲁棒控制器情况类似,因为也是在正负之间跳动,变换频率很高,所以是High Frequency:

可以看到,鲁棒控制器的任务主要是找$\rho (x)>|f(x)|$,确定方案,然后确定是否找$\epsilon$,以及对应值。
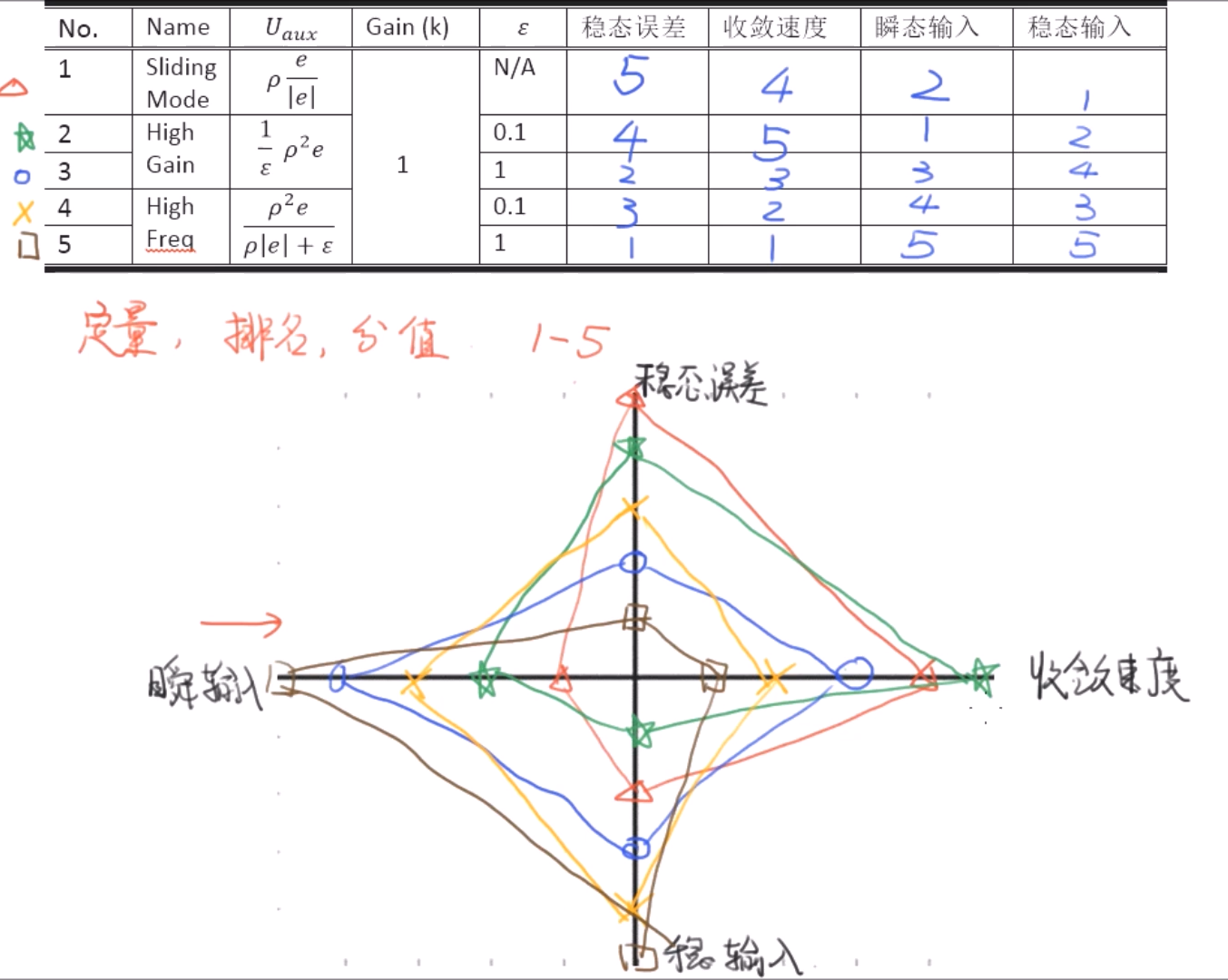
鲁棒控制器分析比较
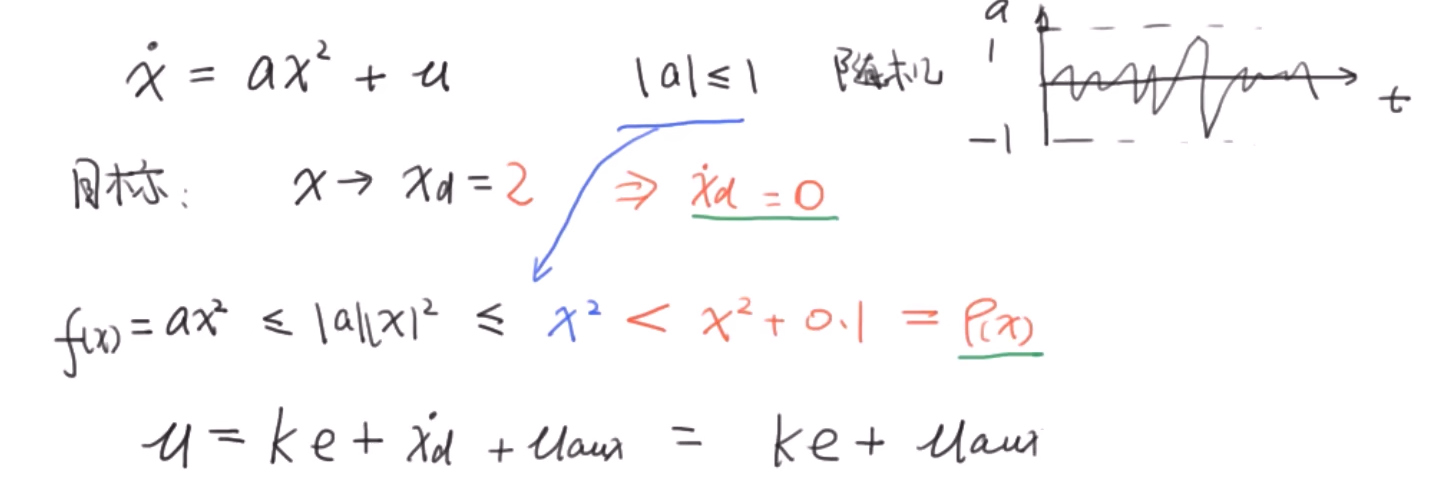
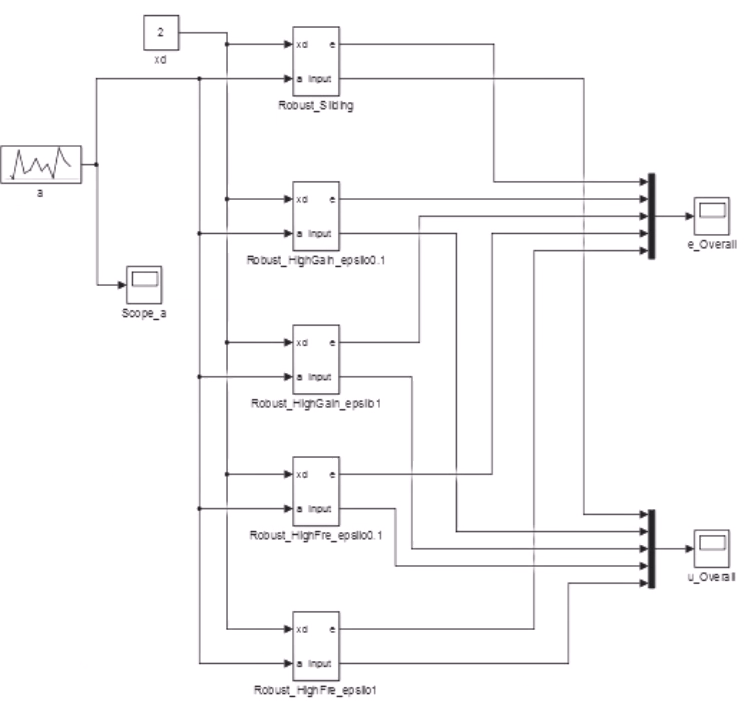
根据题目,我们提供五种控制器方案看实现的效果。
误差时间响应:
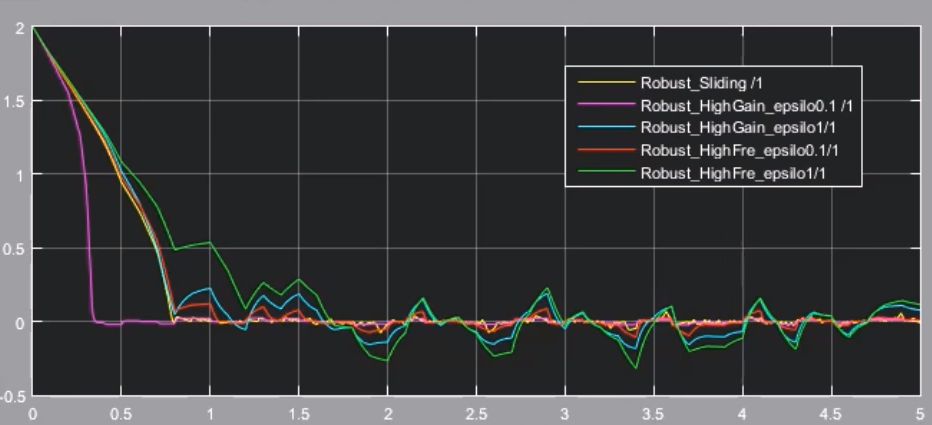
输入:
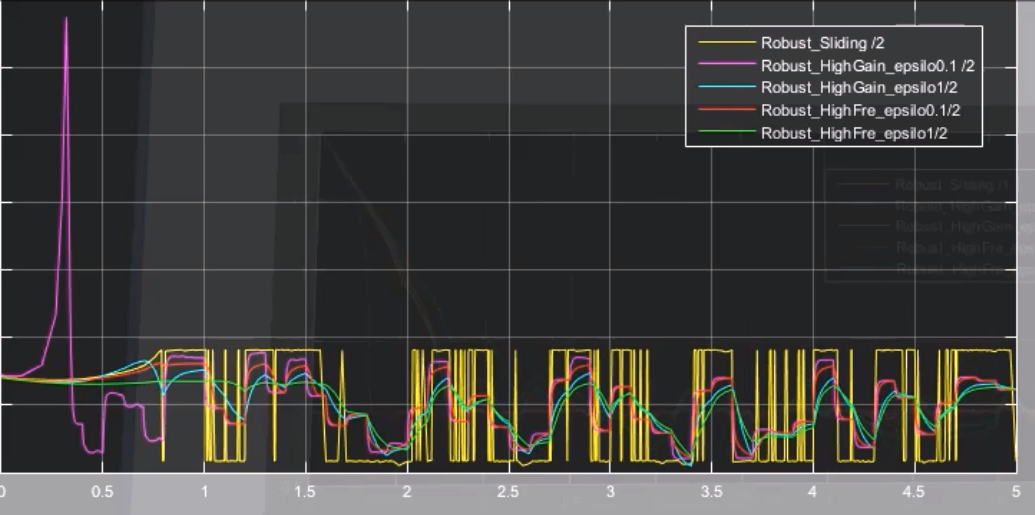
结论: